机器学习中梯度下降法原理及用其解决线性回归问题的C语言实现

本文讲梯度下降（Gradient Descent）前先看看利用梯度下降法进行监督学习（例如分类、回归等）的一般步骤：

1， 定义损失函数（Loss Function）

2， 信息流forward propagation，直到输出端

3， 误差信号back propagation。采用“链式法则”，求损失函数关于参数Θ的梯度

4， 利用最优化方法（比如梯度下降法），进行参数更新

5， 重复步骤2、3、4，直到收敛为止

所谓损失函数，就是一个描述实际输出值和期望输出值之间落差的函数。有多种损失函数的定义方法，常见的有均方误差（error of mean square）、最大似然误差（maximum likelihood estimate）、最大后验概率（maximum posterior probability）、交叉熵损失函数（cross entropy loss）。本文就以均方误差作为损失函数讲讲梯度下降的算法原理以及用其解决线性回归问题。在监督学习下，对于一个样本，它的特征记为x（如果是多个特征，x表示特征向量），期望输出记为t（t为target的缩写），实际输出记为o（o为output的缩写）。两者之间的误差e可用下式表达（为了节省时间，各种算式就用手写的了）：

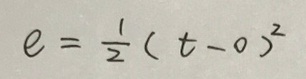
前面的系数1/2主要是为了在求导时消掉差值的平方项2。如果在训练集中有n个样本，可用E来表示所有样本的误差总和，并用其大小来度量模型的误差程度，如下式所示：

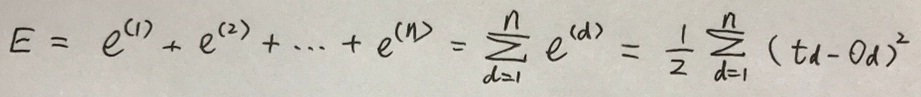
对于第d个实例的输出可记为下式：

对于特定的训练数据集而言， 只有Θ是变量，所以E就可以表示成Θ的函数，如下式：

所以，对于神经网络学习的任务，就是求到一系列合适的Θ值，以拟合给定的训练数据，使实际输出尽可能接近期望输出，使得E取得最小值。

再来看梯度下降。上式中损失函数E对权值向量Θ的梯度如下式所示：

它确定了E最快上升的方向。在梯度前面加上负号“-”，就表示E最快下降的方向。所以梯度下降的训练法则如下式所示：

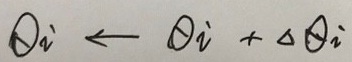， 其中

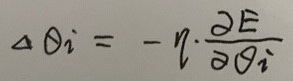
这里的负号“-”表示和梯度相反的方向。η表示学习率。下面给出各个权值梯度计算的数学推导：

所以最终的梯度下降的训练法则如下式：

这个式子就是用于程序中计算参数Θ的。

下面看怎么用梯度下降法解决线性回归问题。线性回归就是能够用一个直线较为精确地描述数据之间的关系。这样当出现新的数据的时候，就能够预测出一个简单的值。线性回归函数可写成 。线性回归问题常用最小二乘法解决，这里用梯度下降法解决主要是通过实例加深对梯度下降法的理解。先假设Y = 2X + 3=2*X + 3*1，取X的四个值分别为1，4，5，8，相应的Y为5，11，13，19。这样就可以描述为有四个样本分别为（1,1），（4,1），（5,1），（8,1），对应的期望值是5，11，13，19.5（这个值做了微调，从19变成了19.5，是为了让四个样本不在一根直线上）。通过梯度下降法求Θ值(最终Θ逼近2和3)。C语言实现的代码如下：

#include <stdio.h>
#include <stdlib.h>

int main(int argc, char *argv[])
{
    double matrix[][]={{,},{,},{,},{,}};   //样本
    double result[]={,,,19.5};                 //期望值
    double err_sum[] = {,,,};                   //各个样本的误差
    double theta[] = {,};                         //Θ,初始值随机
    double err_square_total = 0.0;                   //方差和
    double learning_rate = 0.01;                     //学习率
    int ite_num;                                     //迭代次数

    for(ite_num = ; ite_num <= ; ite_num++)
    {
        int i,j,k;
        err_square_total = 0.0; 

        for(i = ; i < ; i++)
        {
            double h = ;
            for(j = ; j < ; j++)
                h += theta[j]*matrix[i][j];    

            err_sum[i] = result[i] - h;
            err_square_total += 0.5*err_sum[i]*err_sum[i];
        }

        if(err_square_total < 0.05)  //0.05表示精度
             break;

        for(j = ; j < ; j++)
        {
            double sum = ;
            for(k = ; k < ; k++)   //所有样本都参与计算
                sum += err_sum[k]*matrix[k][j];
            theta[j] = theta[j] + learning_rate*sum; //根据上面的公式计算新的Θ
        }
    }

    printf(" @@@ Finish, ite_number:%d, err_square_total:%lf, theta[0]:%lf, theta[1]:%lf\n", ite_num, err_square_total, theta[], theta[]);

    return ;
}

程序运行后的结果为：@@@ Finish, ite_number:308, err_square_total:0.049916, theta[0]:2.037090, theta[1]:3.002130。发现迭代了308次，最终的线性方程为Y=2.037090X + 3.002130，是逼近2和3的。当再有一个新的X时就可以预测出Y了。学习率是一个经验值，一般是0.01--0.001，当我把它改为0.04再运行时就不再收敛了。

上面的梯度下降叫批量梯度下降法（Batch Gradient Descent, BGD）, 它是指在每一次迭代时使用所有样本来进行梯度的更新。当样本数目很大时，每迭代一步都需要对所有样本计算，训练过程会很慢。于是人们想出了随机梯度下降法（Stochastic Gradient Descent, SGD），每次只随机取一个样本计算梯度，训练速度变快了，但是迭代次数变多了（表示不是一直向最快方向下降，但总体上还是向最低点逼近）。还是上面的例子，只不过每次只从四个样本中随机取一个计算梯度。C语言实现的代码如下：

#include <stdio.h>
#include <stdlib.h>

int main(int argc, char *argv[])
{
    double matrix[][]={{,},{,},{,},{,}};  //样本
    double result[]={,,,19.5};                //期望值
    double err_sum[] = {,,,};                  //各个样本的误差
    double theta[] = {,};                        //Θ,初始值随机
    double err_square_total = 0.0;                  //方差和
    double learning_rate = 0.01;                    //学习率
    int ite_num;                                    //迭代次数

    for(ite_num = ; ite_num <= ; ite_num++)
    {
        int i,j,seed;
        err_square_total = 0.0;
        for(i = ; i < ; i++)
        {
            double h = ;
            for(j = ; j < ; j++)
                h += theta[j]*matrix[i][j];    
            err_sum[i] = result[i] - h;
            err_square_total += 0.5*err_sum[i]*err_sum[i];
        }

        if(err_square_total < 0.05)
            break;

        seed = rand()%;
        for(j = ; j < ; j++)
            theta[j] = theta[j] + learning_rate*err_sum[seed]*matrix[seed][j];   //随机选一个样本参与计算
    }

    printf(" @@@ Finish, ite_number:%d, err_square_total:%lf, theta[0]:%lf, theta[1]:%lf\n", ite_num, err_square_total, theta[], theta[]);

    return ;
}

程序运行后的结果为：@@@ Finish, ite_number:1228, err_square_total:0.049573, theta[0]:2.037240, theta[1]:3.000183。发现迭代了1228次（迭代次数变多了），最终的线性方程为Y=2.037240X + 3.000183，也是逼近2和3的。

后来人们又想出了在BGD和SGD之间的一个折中方法，即mini-batch SGD方法，即每次随机的取一组样本来计算梯度。mini-batch SGD是实际使用中用的最多的。还是上面的例子，只不过每次只从四个样本中随机取两个作为一组个计算梯度。C语言实现的代码如下：

#include <stdio.h>
#include <stdlib.h>

int main(int argc, char *argv[])
{
    double matrix[][]={{,},{,},{,},{,}};
    double result[]={,,,19.5};
    double err_sum[] = {,,,};
    double theta[] = {,};
    double err_square_total = 0.0;
    double learning_rate = 0.01;
    int ite_num;

    for(ite_num = ; ite_num <= ; ite_num++)
    {
        int i,j,k,seed;
        err_square_total = 0.0; 
        for(i = ;i<;i++)
        {
            double h = ;   
 
            for(j = ; j < ; j++)
                h += theta[j]*matrix[i][j];    

            err_sum[i] = result[i] - h;
            err_square_total += 0.5*err_sum[i]*err_sum[i];
        }

        if(err_square_total < 0.05)
            break;

        seed = rand()%;
        k = (seed +)%;
        for(j = ; j < ; j++)
        {
            double sum = ;
            sum += err_sum[seed]*matrix[seed][j];   //随机取两个作为一组计算梯度
            sum += err_sum[k]*matrix[k][j];
 
            theta[j] = theta[j] + learning_rate*sum;
        }
    }

    printf(" @@@ Finish, ite_number:%d, err_square_total:%lf, theta[0]:%lf, theta[1]:%lf\n", ite_num, err_square_total, theta[], theta[]);

    return ;
}

程序运行后的结果为： @@@ Finish, ite_number:615, err_square_total:0.047383, theta[0]:2.039000, theta[1]:2.987382。发现迭代了615次，最终的线性方程为Y=2.039000X + 2.987382，也是逼近2和3的。迭代次数介于BGD和SGD中间。在用mini-batch SGD时batch size的选择很关键。