[考试反思]0916csp-s模拟测试44：可笑

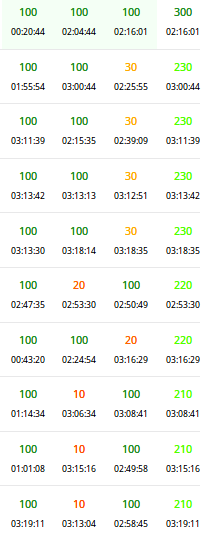
出现了有史以来第一个3首杀AK啊。。。然而跟我没有丝毫关系

（曾经还是有一次考试差点就有那么一点关系的。。。）

然而反正我考得很水就是了。不是很垃圾，而是很水。

这套题是真的水。。。

T1不会证复杂度，但是A掉了，数据很难造所以对拍基本上是白打了。。。

复杂度是对的。数据很水。

T2的话想了挺久，想到要分两种情况讨论，一种简单贪心即可，另一种比较复杂。

考场上没有发现单调性于是复杂度n²了。

但是数据水的过分只要打出来第一种就行了，极其荒谬，样例都不过就能A。

当然我两种情况都打了，复杂度也没被卡。

%%%kx只打了复杂的第二种情况，但是垃圾测试点之留下了他爆搜的10分，RP++;

T3暴力dp对了但是没读入。不知怎么的反正过样例了

我自己都要笑死了。。。。

如果读入了就是230了rank2呢。。。哪里有什么如果

一定要手模样例，尤其在出题人只给了一个小样例的时候

T1：D

比较简单。做成了STL题。

用vector维护每一个因数连续出现的最早位置。用map维护每一个因数在vector里的下标。

打麻烦了。

复杂度O(n log²n)

 #include<cstdio>
 #include<vector>
 #include<map>
 using namespace std;
 vector<int>v[],p[];
 map<int,int>m;
 int gcd(int a,int b){while(b)b^=a^=b^=a%=b;return a;}
 int n,a[];long long ans;
 int main(){//freopen("1.in","r",stdin);freopen("co.out","w",stdout);
     scanf("%d",&n);
     for(int i=;i<=n;++i)scanf("%d",&a[i]);
     v[].push_back(a[]);p[].push_back();ans=a[];
     for(int i=;i<=n;++i){
         for(int j=;j<v[i&^].size();++j){
             int G=gcd(a[i],v[i&^][j]),M=m[G],P=p[i&^][j];
             if(M)P=p[i&][M-]=min(p[i&][M-],P);
             else v[i&].push_back(G),p[i&].push_back(P),m[G]=v[i&].size();
             ans=max(ans,1ll*G*(i-P+));
         }
         ans=max(ans,1ll*a[i]);
         if(m.find(a[i])==m.end())v[i&].push_back(a[i]),p[i&].push_back(i);
         m.clear();
         v[i&^].clear();p[i&^].clear();
     }
     printf("%lld\n",ans);
 }

思路积累：

• 相邻项取gcd以取代枚举所有因子
• 只保存较大的因子，让较大的因子在后面需要的时候再分解成小因子

T2：E

两种情况。所有球里面的最大值$T_{max}$和最小值$T_{min}$要么是不同的颜色，要么在一起。

对于第一种情况式子是$(T_{max} - R_{min})*(B_{max} - T_{min})$

那么就把大的求放进左边，小的放进右边。

第二种情况是$(T_{max} - T_{min})*(R_{max} - R_{min})$

这时候左边就相当于垃圾桶，所有不要的值都往里面扔就是了。

目标就是在每一对球里选一个，使选出的球极差尽量小。

枚举$R_{min}$在考虑我们能否进行决策。

那就是如果一对球里小的那一个大于等于$R_{min}$那么就选小的，否则就选大的。

如果大的球也比$R_{min}$小那么这个就不合法了，更大的$R_{min}$也就不合法了。跳出。

这是O(n²)的。

但是如果我们从小到大枚举$R_{min}$的话，可以发现决策的变化就是把几个小球变成了大球。

那么每对球至多变化一次，单调指针扫的话总复杂度O(n)。

粘考场的O(n²)代码了。

 #include<cstdio>
 #include<algorithm>
 #include<ctime>
 using namespace std;
 struct ps{
     int w,opt;
     friend bool operator<(ps a,ps b){
         return a.w<b.w||(a.w==b.w&&a.opt>b.opt);
     }
 }p[];
 int l[],r[],n,mxmx,mxmn=1e9,mnmx,mnmn=1e9;long long ans;
 int main(){
     scanf("%d",&n);
     for(int i=;i<=n;++i)scanf("%d%d",&l[i],&r[i]);
     for(int i=;i<=n;++i)if(l[i]>r[i])l[i]^=r[i]^=l[i]^=r[i];
     for(int i=;i<=n;++i)mxmx=max(mxmx,r[i]),mxmn=min(mxmn,r[i]),mnmx=max(mnmx,l[i]),mnmn=min(mnmn,l[i]);
     ans=1ll*(mxmx-mxmn)*(mnmx-mnmn);
     for(int i=;i<=n;++i)p[i].w=l[i],p[n+i].w=r[i],p[i].opt=;
     sort(p+,p+n+n+);p[].opt=;
     for(int j=;p[j-].opt&&clock()<;++j){
         int mnn=p[j].w,mxx=;//printf("%d\n",mnn);
         for(int i=;i<=n;++i)if(l[i]>=mnn)mxx=max(mxx,l[i]);else mxx=max(mxx,r[i]);
         ans=min(ans,1ll*(mxmx-mnmn)*(mxx-mnn));
     }
     printf("%lld\n",ans);
 }

思路积累：

• 贪心。
• 单调指针：决策的连续性。
• 分类讨论。

T3：F

首先要想到O(n²)的dp。

刚开始是想的三维，存第几轮时两个指针分别的位置。

然而其实完成一个指令后其中一个指针一定在目标处，记录另一个指针即可。

然后dp式子可以看出是区间加，单点修改，区间取min。

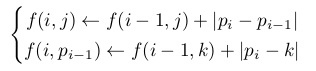
第一个式子直接区间加，第二个式子就是单点取min。

因为带绝对值所以拆开，左边的问f-j，右边的问f+j，两者取min后单点修改。

线段树。过程量爆int了。

记得读入。

 #include<cstdio>
 #include<iostream>
 #include<cmath>
 using namespace std;
 #define int long long
 int w[][],cl[],cr[],n,Q,q[],b,lz[];
 void build(int p,int l,int r){
     cl[p]=l;cr[p]=r;
     if(l==r){
         if(l==b)w[p][]=,w[p][]=-l,w[p][]=l;
         else w[p][]=w[p][]=w[p][]=1e16;
         return;
     }
     build(p<<,l,l+r>>);build(p<<|,(l+r>>)+,r);
     for(int opt=;opt<=;++opt)w[p][opt]=min(w[p<<][opt],w[p<<|][opt]);
 }
 void down(int p){
     for(int opt=;opt<=;++opt)w[p<<][opt]+=lz[p],w[p<<|][opt]+=lz[p];
     lz[p<<]+=lz[p];lz[p<<|]+=lz[p];
     lz[p]=;
 }
 void set(int p,int pos,int W){
     if(cl[p]==cr[p]){
         if(W<w[p][])w[p][]=W,w[p][]=W-pos,w[p][]=W+pos;
         return;
     }
     if(lz[p])down(p);
     if(pos<=cr[p<<])set(p<<,pos,W);
     else set(p<<|,pos,W);
     for(int opt=;opt<=;++opt)w[p][opt]=min(w[p<<][opt],w[p<<|][opt]);
 }
 void add(int p,int l,int r,int W){
     if(l<=cl[p]&&cr[p]<=r){
         lz[p]+=W;
         for(int opt=;opt<=;++opt)w[p][opt]+=W;
         return;
     }
     if(lz[p])down(p);
     if(l<=cr[p<<])add(p<<,l,r,W);
     if(r>=cl[p<<|])add(p<<|,l,r,W);
     for(int opt=;opt<=;++opt)w[p][opt]=min(w[p<<][opt],w[p<<|][opt]);
 }
 int ask(int p,int l,int r,int opt){
     if(l<=cl[p]&&cr[p]<=r)return w[p][opt];
     if(lz[p])down(p);
     return min(l<=cr[p<<]?ask(p<<,l,r,opt):1e16,r>=cl[p<<|]?ask(p<<|,l,r,opt):1e16);
 }
 main(){
     scanf("%lld%lld%lld%lld",&n,&Q,&q[],&b);
     build(,,n);
     for(int i=;i<=Q;++i)scanf("%lld",&q[i]);
     for(int i=;i<=Q;++i){
         int mn1=ask(,,q[i],),mn2=ask(,q[i],n,);
         add(,,n,abs(q[i]-q[i-]));
         set(,q[i-],min(mn1+q[i],mn2-q[i]));
     }
     printf("%lld\n",ask(,,n,));
 }

思路积累：

• 线段树优化dp：把操作更新抽象为区间/单点操作，适用于第二维存值域（到现在靠自己一个都没做出来！！！）
• 拆绝对值，左右分别讨论。