[洛谷P1169][题解][ZJOI2007]棋盘制作

我不是题目的说

这道题运用了一种很巧妙的DP方式：悬线法

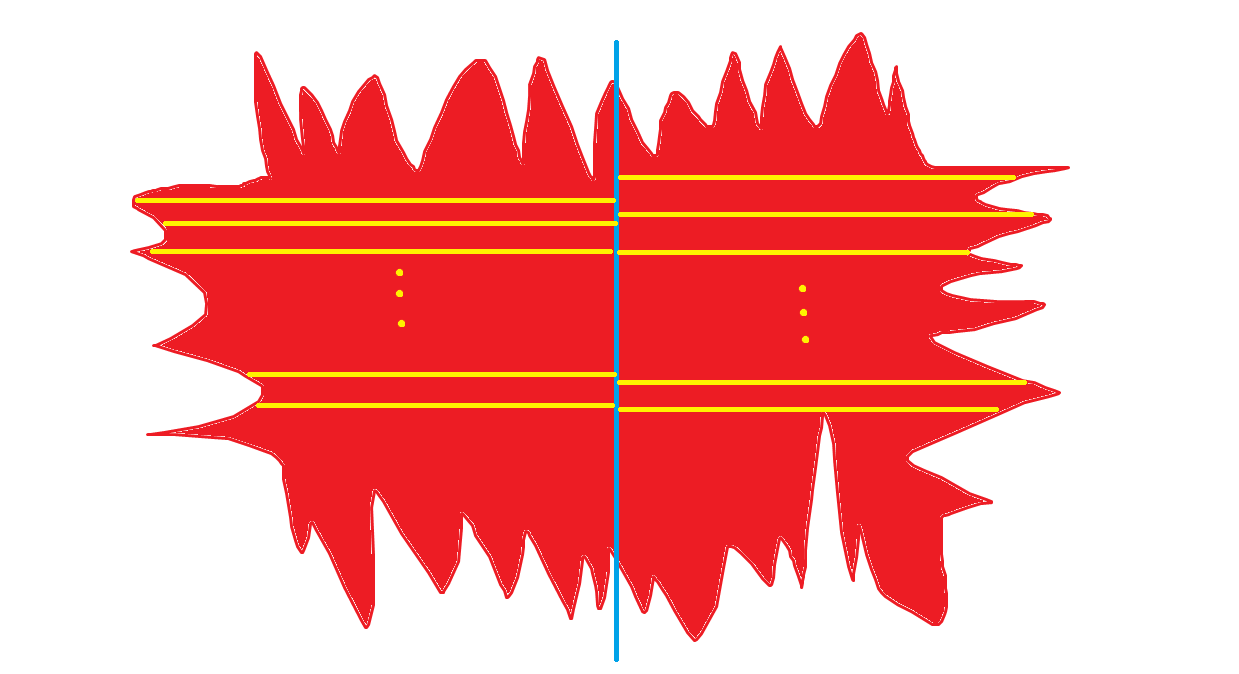
如图，蓝色为悬线，黄色为向两边延伸的长度

那么显然，最大子矩形的宽一定是这些黄线中最小的（证明从略）

所以我们可以维护三个数组：

Up[i][j]表示向上延伸的长度

Left[i][j]表示向左能延伸到的最远横坐标

Right[i][j]表示向右能延伸到的最远横坐标

Code：

 #include<bits/stdc++.h>
 #define INF 0x3f3f3f3f
 using namespace std;
 int n,m,maxRec,maxSqr;
 int mp[][];
 int Up[][];
 int Left[][];
 int Right[][];
 inline void Init(){
     cin>>n>>m;
     for(int i=;i<=n;i++){
         for(int j=;j<=m;j++){
             cin>>mp[i][j];
             //预处理一：没啥可说的
             Left[i][j]=Right[i][j]=j;
             Up[i][j]=;
         }
     }
     //预处理二：处理边界
     for(int i=;i<=n+;i++)mp[i][]=mp[i][m+]=INF;
     for(int j=;j<=m+;j++)mp[][j]=mp[n+][]=INF;
     //预处理三：预处理Left、Right数组（黄线）
     for(int i=;i<=n;i++){
         for(int j=;j<=m;j++){
             if(mp[i][j]!=mp[i][j-]){
                 Left[i][j]=Left[i][j-];
             }
         }
     }
     for(int i=;i<=n;i++){
         for(int j=m-;j>=;j--){
             if(mp[i][j]!=mp[i][j+]){
                 Right[i][j]=Right[i][j+];
             }
         }
     }
 }
 inline void DP(){
     for(int i=;i<=n;i++){
         for(int j=;j<=m;j++){
             //更新
             if(i>&&mp[i][j]!=mp[i-][j]){
                 Up[i][j]=Up[i-][j]+;
                 //注意这里存的是坐标所以Left取max而Right取min
                 Left[i][j]=max(Left[i][j],Left[i-][j]);
                 Right[i][j]=min(Right[i][j],Right[i-][j]);
             }
             //统计矩形，正方形同理
             int dis=Right[i][j]-Left[i][j]+;
             maxRec=max(maxRec,Up[i][j]*dis);
             maxSqr=max(maxSqr,min(Up[i][j],dis)*min(Up[i][j],dis));
         }
     }
     cout<<maxSqr<<endl<<maxRec<<endl;
 }
 int main(){
     Init();
     DP();
     return ;
 }