[Scikit-learn] 4.3 Preprocessing data

数据预处理的两个阶段：

阶段一，理解大纲和常用方法（本篇章内容）。

阶段二，过一遍最新版本的文档。

Ref: 4.4 基于TensorFlow理解三大降维技术：PCA、t-SNE 和自编码器

Ref: 5.3. Preprocessing data【the latest version】

4.3. 数据预处理

• 4.3.1. 标准化、去均值、方差缩放(variance scaling)
  • 4.3.1.1. 特征缩放至特定范围
  • 4.3.1.2. 稀疏数据缩放
  • 4.3.1.3. 含异常值数据缩放
  • 4.3.1.4. 核矩阵中心化
• 4.3.2. 规范化
• 4.3.3. 二值化
  • 4.3.3.1. 特征二值化
• 4.3.4. 分类特征编码
• 4.3.5. 缺失值处理（Imputation）
• 4.3.6. 多项式特征生成
• 4.3.7. 装换器定制

一般性策略

---

原文链接：https://blog.csdn.net/weixin_41990278/article/details/94860020

4.3.1. 标准化、去均值、方差缩放(variance scaling)

4.3.1.1. 特征缩放至特定范围

一、原理

正态分布：如果单个特征没有或多或少地接近于标准正态分布，那么它可能并不能在项目中表现出很好的性能。因为常见分布的极限分布是正态分布。

中心化：减去均值。

缩放：除以非常量特征(non-constant features)的标准差。

二、默认常见假设

例如, 许多学习算法中目标函数的基础都是假设：Ref: http://blog.csdn.net/dream_angel_z/article/details/49406573

• • 所有的特征都是零均值并且具有同一阶数上的方差　(比如径向基函数、支持向量机以及L1, L2正则化项等)。
  • 没有突出的大方差：如果某个特征的方差比其他特征大几个数量级，那么它就会在学习算法中占据主导位置，导致学习器并不能像我们说期望的那样，从其他特征中学习。

三、归一化后有两个好处

Ref: 数据标准化/归一化normalization

1. 提升模型的 "收敛速度"

如下图，x₁的取值为0-2000，而x₂的取值为1-5，假如只有这两个特征，对其进行优化时，会得到一个窄长的椭圆形，导致在梯度下降时，梯度的方向为垂直等高线的方向而走之字形路线，这样会使迭代很慢，相比之下，右图的迭代就会很快。

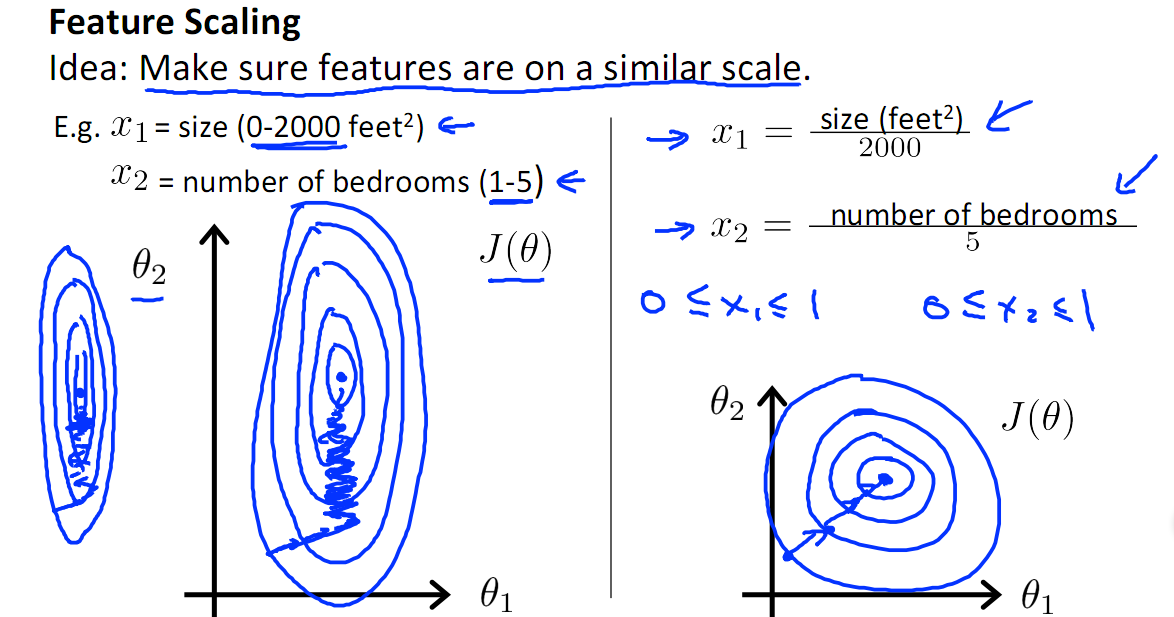
2. 提升模型的 "精度"

归一化的另一好处是提高精度，这在涉及到一些距离计算的算法时效果显著，比如算法要计算欧氏距离，上图中x2的取值范围比较小，涉及到距离计算时其对结果的影响远比x1带来的小，所以这就会造成精度的损失。

所以归一化很有必要，他可以使各个特征对结果做出的贡献相同。

在多指标评价体系中，由于各评价指标的性质不同，通常具有不同的量纲和数量级。当各指标间的水平相差很大时，如果直接用原始指标值进行分析，就会突出数值较高的指标在综合分析中的作用，相对削弱数值水平较低指标的作用。

因此，为了保证结果的可靠性，需要对原始指标数据进行标准化处理。

在数据分析之前，我们通常需要先将数据标准化（normalization），利用标准化后的数据进行数据分析。数据标准化也就是统计数据的指数化。数据标准化处理主要包括数据同趋化处理和无量纲化处理两个方面。

• • 数据同趋化处理主要解决不同性质数据问题，对不同性质指标直接加总不能正确反映不同作用力的综合结果，须先考虑改变逆指标数据性质，使所有指标对测评方案的作用力同趋化，再加总才能得出正确结果。
  • 数据无量纲化处理主要解决数据的可比性。

经过上述标准化处理，原始数据均转换为无量纲化指标测评值，即各指标值都处于同一个数量级别上，可以进行综合测评分析。

In a nutshell

从经验上说，归一化是让不同维度之间的特征在数值上有一定比较性，可以大大提高分类器的准确性。

四、代码演示

标准化样本数据的“特征列"

from sklearn import preprocessing
import numpy as np

X = np.array([[ 1., -1.,  2.],
              [ 2.,  0.,  0.],
              [ 0.,  1., -1.]])

X_scaled =preprocessing.scale(X)
X_scaled
array([[ 0.        , -1.22474487,  1.33630621],
       [ 1.22474487,  0.        , -0.26726124],
       [-1.22474487,  1.22474487, -1.06904497]])
X_scaled.mean(axis=0)
X_scaled.std(axis=0)

可见，这里将矩阵的纵列标准化，而不是对整个矩阵。

经过StandardScaler之后，横坐标与纵坐标的分布出现了很大的差异，这可能是outliers造成的。

去除outliers是一个后续探讨的问题。

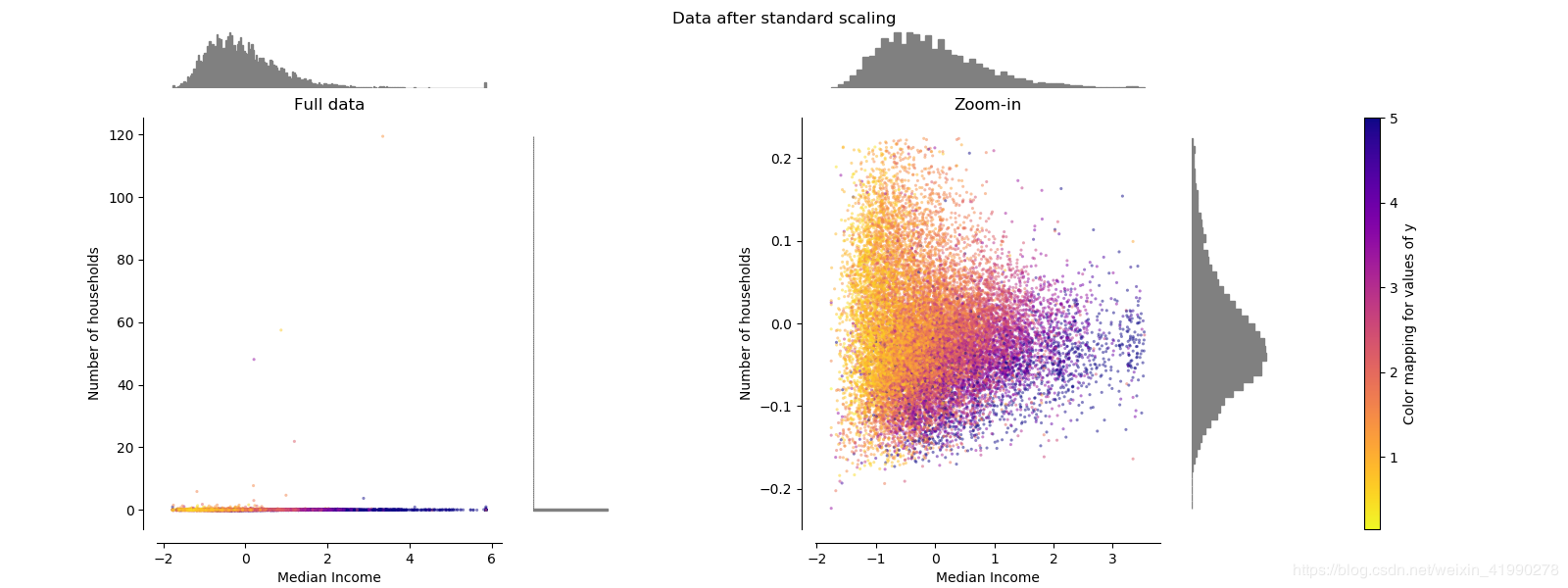
缩放至特定范围

(1) 映射到 [0，1] - MinMaxScaler

X_train = np.array([[ 1., -1.,  2.],
                    [ 2.,  0.,  0.],
                    [ 0.,  1., -1.]])

min_max_scaler =preprocessing.MinMaxScaler()
X_train_minmax = min_max_scaler.fit_transform(X_train)
X_train_minmax
#array([[ 0.5       ,  0.        ,  1.        ],
#       [ 1.        ,  0.5       ,  0.33333333],
#       [ 0.        ,  1.        ,  0.        ]])
min_max_scaler.scale_
min_max_scaler.min_

# 训练部分数据，得到变换method，再用到test数据中，这样更高效些
X_test = np.array([[ -3., -1., 4.]])
X_test_minmax = min_max_scaler.transform(X_test)
X_test_minmax

例如：假定属性income的最小与最大值分别为$12,000和$98,000。我们想映射income到区间[0,1]。

根据min-max标准化，income值$73,600将变换为（73,600-12,000）/（98,000-12,000）×（1-0）=0.716。

(2) 映射到 [-1，1] - MaxAbsScaler

X_train = np.array([[ 1., -1.,  2.],
                    [ 2.,  0.,  0.],
                    [ 0.,  1., -1.]])
max_abs_scaler = preprocessing.MaxAbsScaler()
X_train_maxabs = max_abs_scaler.fit_transform(X_train)
X_train_maxabs                # doctest +NORMALIZE_WHITESPACE^
#array([[ 0.5, -1. ,  1. ],
#       [ 1. ,  0. ,  0. ],
#       [ 0. ,  1. , -0.5]])

# 训练部分数据，得到变换method，再用到test数据中，这样效率高些
X_test = np.array([[ -3., -1.,  4.]])
X_test_maxabs = max_abs_scaler.transform(X_test)
X_test_maxabs
max_abs_scaler.scale_    

(3) [0, 1] 还是 [-1, 1] ?

假设我们有一个只有一个hidden layer的多层感知机（MLP）的分类问题。每个hidden unit表示一个超平面，每个超平面是一个分类边界。参数w（weight）决定超平面的方向，参数b（bias）决定超平面离原点的距离。如果b是一些小的随机参数（事实上，b确实被初始化为很小的随机参数），那么所有的超平面都几乎穿过原点。所以，如果data没有中心化在原点周围，那么这个超平面可能没有穿过这些data，也就是说，这些data都在超平面的一侧。这样的话，局部极小点（local minima）很有可能出现。 所以，在这种情况下，标准化到[-1, 1]比[0, 1]更好。

五、经验总结

1、在分类、聚类算法中，需要使用距离来度量相似性的时候、或者使用PCA技术进行降维的时候，StandardScaler表现更好。

2、在不涉及距离度量、协方差计算、数据不符合正太分布的时候，可以使用MinMaxScaler。比如图像处理中，将RGB图像转换为灰度图像后将其值限定在[0 255]的范围。

量纲、去量纲

原因是使用MinMaxScaler，其协方差产生了倍数值的缩放，因此这种方式无法消除量纲对方差、协方差的影响，对PCA分析影响巨大；同时，由于量纲的存在，使用不同的量纲、距离的计算结果会不同。

而在StandardScaler中，新的数据由于对方差进行了归一化，这时候每个维度的量纲其实已经等价了，每个维度都服从均值为0、方差1的正态分布，在计算距离的时候，每个维度都是去量纲化的，避免了不同量纲的选取对距离计算产生的巨大影响。
数据处理的时候除了数据清洗，离群值处理等，往往还需要一些数据变换的方法。

数据标准化/去量纲的几种方法

（以下内容涉及到的一些概念，在后续章节学习）

去量纲指的的去除数据单位之间的不统一，将数据统一变换为无单位(统一单位)的数据集，也可以作为指标的权重，进行后续的加权计算，这点在日常有诸多应用。

在确定指标权重时，应先对数据进行清洗，权重的确定过程应该更靠近建模或者结果输出部分，确定指标权重时，需要考虑指标是否有负值、所采取方法分母是否为0、正负向指标划分等情况。

指标权重的确定有主观、客观和混合三类。

经验权重法为主观方法。主成分/因子分析、信息量（变异系数）、独立性（多元回归分析）、相关系数法为客观权重法。

RSR（秩和比）和层次分析法（AHP）、Delphi、专家排序、算数均值组合（均数法）、连乘累积组合（累积法）采取主客观混合使用。本文主要讨论客观权重法。

经验权重法由转接或主负责人根据评价指标的重要性来确定权重。

主成分/因子分析，利用方差最大正交旋转法，得到特征根大于等于1的共性因子，计算共性因子的累计贡献率确定权重，累积贡献率越大，权重越大。

独立性权重法，采用多元回归分析方法，计算复相关系数确定权重，以每项指标为因变量，以其他指标为自变量，计算复相关系数，得到各指标对应的复相关系数，复相关系数越大，重复信息越多，权重应该越小，故可取倒数作为权重得分。

权重稳定性检验（暂时不考虑），权重是经过统计得到的频数分布中的频率，在抽样统计中，每一权重变动在 5-10个百分点之间，综合评价z值与原z值排序结果一致，说明权重在该系统是稳定的。

以下是一些常用方法，各种方法的适用环境还需要多多尝试和摸索，我在这里也会根据自己的工作情况，更新各种方法的使用心得。

线性比例变换：正逆向指标都变为正向；所有指标都是非负数，逆向指标处理为非线性变换。

向量归一化（列模为1）：考虑了指标差异性；正逆指标方向无变化，不能消除负值。

极差变换法：正逆指标方向一致，全变为正值；忽略了指标差异性。

Z值法/标准样本变换法：样本标准正态化；负值，正逆指标方向无变化

六、规范化

辨析：

标准化 (归一化)，正则化，规范化

1.normalization - 通常是减去均值后再除以方差。
2.regularization - 通常是指，为防止模型overfit ,在参数上做的抑制。如L2 regularization.在正常损失上加上L2部分。
3.normalize - 将向量除以它的"长度""，做成单位向量。

 

作用：

规范化是使单个样本具有单位范数的缩放操作，计算 "样本对的相似性"。

这个在你使用二次型，比如点积或者其他核去定量计算任意样本对之间的相似性时是非常有用的。

规范化是向量空间模型 <http://en.wikipedia.org/wiki/Vector_Space_Model> 的基本假设，经常在文本分类和聚类当中使用。

思想：

normalize 主要思想是对每个样本计算其p-范数，

然后对该样本中每个元素除以该范数，

这样处理的结果是使得每个处理后样本的p-范数 (L1-norm, L2-norm) 等于1。

X = [[ 1., -1.,  2.],
     [ 2.,  0.,  0.],
     [ 0.,  1., -1.]]

X_normalized = preprocessing.normalize(X, norm='l1')
X_normalized    

array([[ 0.25, -0.25,  0.5 ],
       [ 1.  ,  0.  ,  0.  ],
       [ 0.  ,  0.5 , -0.5 ]])

X_normalized = preprocessing.normalize(X, norm='l2')
X_normalized 

array([[ 0.40824829, -0.40824829,  0.81649658],
       [ 1.        ,  0.        ,  0.        ],
       [ 0.        ,  0.70710678, -0.70710678]])

或者，先创建个对象，让这个对象去处理数据。

normalizer = preprocessing.Normalizer().fit(X)
normalizer.transform(X)
normalizer.transform([[-1.,  1., 0.]])

特殊化策略

---

一、数据量不大

• 稀疏数据缩放

数据量多，趋向于正态分布；那数据量少（稀疏）时，怎么办？

稀疏数据的中心化会破坏数据中的稀疏结构，因此很少有一个比较明智的实现方式。

MaxAbsScaler【推荐】

但是，对稀疏输入进行缩放操作是有意义的，特别是当特征的数值并不在同一个量级上面的时候。 MaxAbsScaler 和:func:maxabs_scale 是稀疏数据缩放比较推荐的实现方式。

中心化破坏稀疏性【小心】

但是，scale 和 StandardScaler 可以接收``scipy.sparse``矩阵作为输入,只要将参数``with_centering=False``传入构造函数。

否则程序将会出现异常 ValueError 。 因为默认的中心化操作会破坏数据的稀疏性，并导致大量的内存占用。

异常值 与 稀疏性【不适用】

RobustScaler 并不适用于稀疏数据，但是你可以在稀疏输入上使用the ``transform``方法。

注意，缩放器既可以接收行压缩稀疏数据也可以是列压缩稀疏数据(参见``scipy.sparse.csr_matrix``和``scipy.sparse.csc_matrix``)。 其他形式的稀疏输入**会被转换为行压缩稀疏表示**。为了避免不必要的内存复制，推荐在顶层使用CSR或CSC表示。

最后，如果已经中心化的数据并不是很大，可以选择使用’‘toarray’‘方法将稀疏矩阵转换为数组。

二、异常值较多

• 含异常值数据缩放

如果你的数据包含较多的异常值，使用均值和方差缩放可能并不是一个很好的选择。

在这种情况下，你可以使用robust_scale 和:class:RobustScaler 作为替代。它们使用更加鲁棒的中心和范围估计来缩放你的数据。

三、缺失值较多

4.3.5. 缺失值处理（Imputation）

处理缺失数值的一个更好的策略就是从已有的数据推断出缺失的数值。

缺失数值处理的基本策略，比如使用缺失数值所在行或列的均值、中位数、众数来替代缺失值。该类也兼容不同的缺失值编码。

# 缺失值被编码为``np.nan``, 使用包含缺失值的列的均值来替换缺失值。
import numpy as np
from sklearn.preprocessing import Imputer
imp = Imputer(missing_values='NaN', strategy='mean', axis=0)
imp.fit([[1, 2], [np.nan, 3], [7, 6]])

Y = [[np.nan, 2], [6, np.nan], [7, 6]]
print(imp.transform(Y))  

上述代码使用数组X去“训练”一个Imputer类，然后用该类的对象去处理数组Y中的缺失值，缺失值的处理方式是使用X中的均值（axis=0表示按列进行）代替Y中的缺失值。

当然也可以使用imp对象来对X数组本身进行处理。

四、多项式特征升维

4.3.6. 多项式特征生成

很多情况下，考虑输入数据中的非线性特征来增加模型的复杂性是非常有效的。

一个简单常用的方法就是使用多项式特征，它能捕捉到特征中高阶和相互作用的项。

特征向量X从:math:(X_1, X_2) 被转换成:math:(1, X_1, X_2, X_1², X_1*X_2, X_2²)。

特征升维效果：

import numpy as np
from sklearn.preprocessing import PolynomialFeatures
X = np.arange(6).reshape(3, 2)
#array([[0, 1],
#       [2, 3],
#       [4, 5]])
poly = PolynomialFeatures(2)
poly.fit_transform(X)
#array([[  1.,   0.,   1.,   0.,   0.,   1.],
#       [  1.,   2.,   3.,   4.,   6.,   9.],
#       [  1.,   4.,   5.,  16.,  20.,  25.]])

将特征多样化后（一个典型的例子），有助于加快training：

仅保留交叉项：

X = np.arange(9).reshape(3, 3)

poly = PolynomialFeatures(degree=3, interaction_only=True)
poly.fit_transform(X)    

通过尝试不同的degree的曲线模型来拟合样本点：

#!/usr/bin/env python
"""
========================
Polynomial interpolation
========================

This example demonstrates how to approximate a function with a polynomial of
degree n_degree by using ridge regression. Concretely, from n_samples 1d
points, it suffices to build the Vandermonde matrix, which is n_samples x
n_degree+1 and has the following form:

[[1, x_1, x_1 ** 2, x_1 ** 3, ...],
 [1, x_2, x_2 ** 2, x_2 ** 3, ...],
 ...]

Intuitively, this matrix can be interpreted as a matrix of pseudo features (the
points raised to some power). The matrix is akin to (but different from) the
matrix induced by a polynomial kernel.

This example shows that you can do non-linear regression with a linear model,
using a pipeline to add non-linear features. Kernel methods extend this idea
and can induce very high (even infinite) dimensional feature spaces.
"""
print(__doc__)

# Author: Mathieu Blondel
#         Jake Vanderplas
# License: BSD 3 clause

import numpy as np
import matplotlib.pyplot as plt

from sklearn.linear_model import Ridge
from sklearn.preprocessing import PolynomialFeatures
from sklearn.pipeline import make_pipeline

def f(x):
    """ function to approximate by polynomial interpolation"""
    return x * np.sin(x)

# generate points used to plot
x_plot = np.linspace(0, 10, 100)

# generate points and keep a subset of them
x = np.linspace(0, 10, 100)
rng = np.random.RandomState(0)
rng.shuffle(x)
x = np.sort(x[:20])
y = f(x)
# 获得此次实验样本
# create matrix versions of these arrays
X = x[:, np.newaxis]
X_plot = x_plot[:, np.newaxis]

plt.plot(x_plot, f(x_plot), label="ground truth")
plt.scatter(x, y, label="training points")

for degree in [3, 4, 5]:
    model = make_pipeline( PolynomialFeatures(degree), Ridge() )　　# pipeline的使用另起一章
    model.fit(X, y)
    y_plot = model.predict(X_plot)
    plt.plot(x_plot, y_plot, label="degree %d" % degree)

plt.legend(loc='lower left')

plt.show()

Result: 

五、白化 sphering

白化是例如pca，ica操作之前的必要数据预处理步骤。

From: http://blog.csdn.net/lizhe_dashuju/article/details/50263339

白化过程

FastICA需要对数据做白化处理。

设x是一个随机变量，存在一个线性变换V将它变换成z：

　　z=Vx

且：

　　E{zz^T}=I

那么，V就是白化变换矩阵。

为何用"白化"

Ref: http://ufldl.stanford.edu/wiki/index.php/%E7%99%BD%E5%8C%96

我们已经了解了如何使用PCA降低数据维度。在一些算法中还需要一个与之相关的预处理步骤，这个预处理过程称为白化（一些文献中也叫sphering）。

举例来说，假设训练数据是图像，由于图像中相邻像素之间具有很强的相关性，所以用于训练时输入是冗余的。

白化的目的就是降低输入的冗余性；更正式的说，我们希望通过白化过程使得学习算法的输入具有如下性质：

(i) 特征之间相关性较低；

(ii) 所有特征具有相同的方差。

详见：UFLDL Tutorial，Preprocessing: PCA and Whitening

• • PCA 【单独详谈】
  • Whitening
  • Implementing PCA/Whitening
  • Exercise:PCA in 2D
  • Exercise:PCA and Whitening

End.