斐波那契数列 51nod

1242 斐波那契数列的第N项

基准时间限制：1 秒 空间限制：131072 KB 分值: 0 难度：基础题

 收藏

 关注

斐波那契数列的定义如下：

 

F(0) = 0

F(1) = 1

F(n) = F(n - 1) + F(n - 2) (n >= 2)

 

(1, 1, 2, 3, 5, 8, 13, 21, 34, 55, 89, 144, 233, 377, ...)

给出n，求F(n)，由于结果很大，输出F(n) % 1000000009的结果即可。

 

Input

输入1个数n(1 <= n <= 10^18)。

Output

输出F(n) % 1000000009的结果。
运用矩阵乘法去做，有矩阵，可以矩阵快速幂求出转移矩阵即可得到结果。

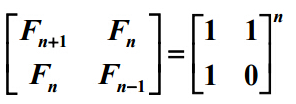
#include<iostream>
#include<algorithm>
#include<cstdio>
using namespace std;
typedef long long LL;
int n = ;
struct mat
{
    LL a[][];
};
mat mul(mat m1,mat m2)
{
    mat ans;
    for(int i=;i<n;i++)
        for(int j=;j<n;j++)
        {
            LL temp = ;
            for(int k=;k<n;k++)
            {
                temp+=m1.a[i][k]*m2.a[k][j];
            }
            ans.a[i][j] = temp % ;
        }
    return ans;
}
mat pow(mat m,LL b)
{
    if(b<=)
        return m;
    mat temp = pow(m,b/);
    if(b&)
        return mul(mul(temp,temp),m);
    else
        return mul(temp,temp);
}
int main()
{
    LL num;
    mat beg;
    beg.a[][]=beg.a[][]=beg.a[][]=;beg.a[][]=;
    cin>>num;
    cout<<pow(beg,num-).a[][]<<endl;
    return ;
}

1031 骨牌覆盖

基准时间限制：1 秒 空间限制：131072 KB 分值: 10 难度：2级算法题

 收藏

 关注

在2*N的一个长方形方格中，用一个1*2的骨牌排满方格。

 

问有多少种不同的排列方法。

 

例如：2 * 3的方格，共有3种不同的排法。（由于方案的数量巨大，只输出 Mod 10^9 + 7 的结果）

Input

输入N(N <= 1000)

Output

输出数量 Mod 10^9 + 7

Input示例

3

Output示例

3

显然,N=1时一种方法，N=2时有两种方法。
当N>2，可分为两种情况，1是竖着放，那么方法数目为前n-1个的结果，f(n-1)
2是两个横着放，这样占用了两个格子，方法数目是前n-2个结果 f(n-2)
f(n)=f(n-1)+f(n-2),f(1)=1,f(2)=2;
由上面程序略作修改

#include<iostream>
#include<algorithm>
#include<cstdio>
using namespace std;
typedef long long LL;
int n = ;
#define M 1000000007
struct mat
{
    LL a[][];
};
mat mul(mat m1,mat m2)
{
    mat ans;
    for(int i=;i<n;i++)
        for(int j=;j<n;j++)
        {
            LL temp = ;
            for(int k=;k<n;k++)
            {
                temp+=m1.a[i][k]*m2.a[k][j];
            }
            ans.a[i][j] = temp%M;
        }
    return ans;
}
mat pow(mat m,LL b)
{
    if(b<=)
        return m;
    mat temp = pow(m,b/);
    if(b&)
        return mul(mul(temp,temp),m);
    else
        return mul(temp,temp);
}
int main()
{
    LL num;
    mat beg;
    beg.a[][]=beg.a[][]=beg.a[][]=;beg.a[][]=;
    cin>>num;
    mat tmp;
    tmp.a[][]=,tmp.a[][]=tmp.a[][]=,tmp.a[][]=;
    mat r = pow(beg,num-);
    mat as=mul(tmp,r);
    cout<<as.a[][]<<endl;
    return ;
}

1126 求递推序列的第N项

基准时间限制：1 秒 空间限制：131072 KB 分值: 10 难度：2级算法题

 收藏

 关注

有一个序列是这样定义的：f(1) = 1, f(2) = 1, f(n) = (A * f(n - 1) + B * f(n - 2)) mod 7.

给出A，B和N，求f(n)的值。

 

Input

输入3个数：A,B,N。数字之间用空格分割。(-10000 <= A, B <= 10000, 1 <= N <= 10^9)

Output

输出f(n)的值。

同样思路用矩阵做，注意避免负数的出现 （ans+7）%7.只需把递归式中系数修改。

#include<iostream>
#include<algorithm>
#include<cstdio>
using namespace std;
typedef long long LL;
int n = ;
#define M 1000000007
struct mat
{
    LL a[][];
};
mat mul(mat m1,mat m2)
{
    mat ans;
    for(int i=;i<n;i++)
        for(int j=;j<n;j++)
        {
            LL temp = ;
            for(int k=;k<n;k++)
            {
                temp+=m1.a[i][k]*m2.a[k][j]    ;
            }
            ans.a[i][j] = (temp+)%;
        }
    return ans;
}
mat pow(mat m,LL b)
{
    if(b<=)
        return m;
    mat temp = pow(m,b/);
    if(b&)
        return mul(mul(temp,temp),m);
    else
        return mul(temp,temp);
}
int main()
{
    LL num,t1,t2;
    cin>>t1>>t2>>num;
    mat beg;
    beg.a[][]=t1,beg.a[][]=t2,beg.a[][]=;beg.a[][]=;
    mat r = pow(beg,num-);
    cout<<(r.a[][]+r.a[][]+)%<<endl;
    return ;
}