《University Calculus》-chape4-极坐标与圆锥曲线-极坐标系下的面积与弧长

极坐标系下的面积：

在直角坐标系下一样，这里在极坐标系下，我们面临一个同样的问题：如何求解一个曲线围成的面积？虽然两种情况本质上是一样的，但是还是存在一些细小的区别。

在直角坐标系下中，我们是讨论一条曲线和x轴围成的封闭的曲边梯形的面积。而极坐标系下，我们讨论一条曲线的两个端点与极坐标原点的线段加上该曲线连成的图形的面积。

如下图所示。

笛卡尔系下我们求曲边梯形的面积是用小矩形的面积逼近

而在极坐标系下我们用小扇形的面积进行逼近

极坐标系下曲线的长度：

这里结合之前我们在平面笛卡尔系得到结论：

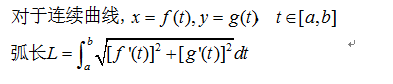
而从笛卡尔系到极坐标系，刚好x、y可以用θ表示成参数形式。