Manacher思想 SCOI2013 密码

关于$\mathrm{Manacher}$算法，网上介绍已经很全面 这里说一下自己的理解

这里的$rad$数组：$rad_i$表示以以位置i为中心的最长回文串的回文半径（不包括i这个点）。

朴素的思想大概是从每个点出发像两边扩展，大概$O(n^2)$复杂度？据说$\mathrm{Manacher}$是$O(n)$的（不会证，Orz，大概因为每个位置只会被暴力扩展$O(1)$次）这是因为回文串有对称性，我们可以利用这点来优化算法。现在假设我们已经得到了$i$和$i$以前的$rad$值，现在想直接通过$O(1)$的时间计算出i右边一些点的$rad$值。设$k$从$1$到$rad_i$，表示现在想直接计算出$rad_{i+k}$的$rad$值。则有下列情况

其中

红色：$rad_i$
橙色：$rad_{i-k}$
绿色：$rad_{i-k}$

①$rad_i-k<rad_{i-k}$————————————————————————————————————————————————————————————

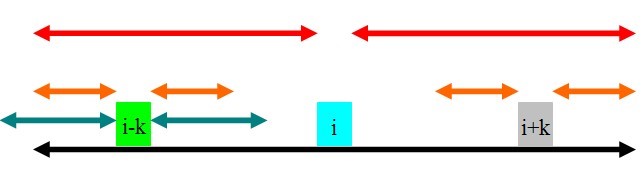
此时$rad_{i+k}$一定为$rad_i-k$否则根据对称性，$rad_i$可以更大。

②$rad_i-k>rad_{i-k}$————————————————————————————————————————————————————————————

此时根据对称性也可以很显然地看出$rad_{i+k}=rad_{i-k}$

由①②有，当$rad_i-k\not=rad_{i-k}$时，$rad_{i+k}=\min{\{rad_{i-k},rad_i-k\}}$

那么$rad_i-k=rad_{i+k}$时怎么办呢

③$rad_i-k=rad_{i-k}$————————————————————————————————————————————————————————————

这时即使$rad_{i+k}>rad_{i-k}$也没有矛盾，此时应当令i+=k用朴素的算法扩大$rad_i$之后再用这个$rad_i$迭代更新。

代码：

for(int i=1,j=0,k;i<=len;){
    for(;s[i-j-1]==s[i+j+1];j++);
    rad[i]=j;
    for(k=1;k<=j && rad[i]-k!=rad[i-k];k++)
        rad[i+k]=min(rad[i]-k,rad[i-k]);
    i+=k;
    j=max(j-k,0);
}

但是这样只能求出长度为奇数的回文串的长度，对于偶数，我们这样处理。

char s[Maxn]={0};
s[0]='*';
for(int i=0;i<_len;i++){
    s[++len]=_s[i];
    s[++len]='#';
}
s[len]='&';

之后再按上面的方法求即可。

然后这里再说一下$\mathrm{SCOI2013}$的密码，用了$\mathrm{Manacher}$的思想。（题目链接http://acm.uestc.edu.cn/#/problem/show/128）

很容易想到朴素的算法，把必须为相同字符的合并为一个集合（用并查集实现），然后对必须不相同的集合连边，从集合向集合中的元素连边。后一步是$O(n)$的，而前一步最坏是$O(n^2)$对于$10^5$的数据显然无法承受，这里很自然想到$\mathrm{Manacher}$的$O(n)$

$i$从$1$开始，维护$rad_i+i$的最大值，为$MX_r$,这样的$i$记为$MX_{id}$,然后显然我们只需要从$i+\max{\{0, \min{\{MX_r-i,rad_{2MX_{id}-i}\}}\}}$开始合并，大概又是$O(n)$的

完整代码

#include<iostream>
#include<cstring>
#include<cstdlib>
#include<cstdio>
#include<algorithm>
#define dout printf
using namespace std;
 
const int Maxn=100000+10;
int n,rad[Maxn*2];
int col[Maxn*2],cannot[Maxn*2][30],cnt=0;
int stk[30],top;
bool instk[Maxn*2];
inline void getint(int&x){
    char c=getchar();
    for(x=0;!isdigit(c);c=getchar());
    for(;isdigit(c);c=getchar())x=x*10+c-'0';
}
struct Edge{int b;Edge*next;}edges[Maxn*3*2],*firc[Maxn*2],*fird[Maxn*2];int tot;
void AddEdge(int a,int b,Edge*fir[]){
    edges[++tot]=(Edge){b,fir[a]};fir[a]=edges+tot;
}
int fa[Maxn*2];
int Find(const int&x){
    return fa[x]==x?x:fa[x]=Find(fa[x]);
}
bool Union(int x,int y){
    x=Find(x),y=Find(y);
    if(x==y)return 0;
    return fa[y]=x,1;
}
void input(){
    getint(n);
    for(int i=1;i<=n;i++)getint(rad[(i<<1)-1]);
    for(int i=1;i<n;i++)getint(rad[i<<1]);
}
 
void work(const int n2=n*2){
    int MX_r=1,MX_id=1;
    char*ans=new char[Maxn];
    memset(ans,0,sizeof(*ans)*Maxn);
    for(int i=1;i<=n2;i++)fa[i]=i;
    for(int i=2;i<=n2;i++){
        for(int j=max(0, min(MX_r-i,rad[MX_id*2-i]) );i-j>0&&i+j<=n2&&j<=rad[i];j++) {
            Union(i-j,i+j);
        }
        if(rad[i]+i>MX_r)MX_r=i+rad[i],MX_id=i;
    }
    for(int f,i=1;f=Find(i),i<=n2;i+=2)
        AddEdge(f,(i+1)>>1,firc);
    for(int f1,f2,d,i=2;i<=n2;i++){
        d=rad[i]+1;
        f1=Find(i-d),f2=Find(i+d);
        AddEdge(f1,f2,fird);
        AddEdge(f2,f1,fird);
    }
    for(int x,real,f,i=1;real=(i+1)>>1,i<=n2;i+=2)if(!ans[real]){
        x=1;f=Find(i);
        for(;cannot[f][x];x++);
        for(Edge*p=fird[f];p;p=p->next)cannot[p->b][x]=1;
        for(Edge*p=firc[f];p;p=p->next)ans[p->b]=x+'a'-1;
    }
    puts(ans+1);
    delete ans;
}
int main(){
    freopen("password.in","r",stdin);
    freopen("password.out","w",stdout);
 
    input();
    work();
 
    return 0;
}