算法马拉松35 E 数论只会Gcd - 类欧几里得 - Stern-Brocot Tree - 莫比乌斯反演

题目传送门

　　传送门

　　这个官方题解除了讲了个结论，感觉啥都没说，不知道是因为我太菜了，还是因为它真的啥都没说。

　　如果 $x \geqslant y$，显然 gcd(x, y) 只会被调用一次。

　　否则考虑每次操作前的数对应该是 $(y, y + kx)$。这样仍然不好处理。考虑忽略掉达到的 $a < b$ 的状态，那么每次的 $k \geqslant 1$。那么当较大数加上较小数的时候对应将 $k$ 加上 1，对应交换两边的数，然后将 $k$ 加上1。特别地，第一次操作不能做大加上小，因为第一次操作的时候没有 $k$。

　　显然每次操作中，数对可以表示为 $(ax + by, cx + dy)$。那么一次加操作会得到 $(a + c) x , (c + d) y$，你发现这个东西和 SBT 的构造有点像。考虑把这个操作对应到 SBT 上。在两个相邻分数 $a, b$ 中插入一个分数 $c$ 可以得到新的两对 $a, c$ 和 $(c, b)$，分别可以看右加上左边以及左边加上右边。

　　暂时不考虑 $m$ 的限制，我们来简单说明一下满足除了初始的数对一个数对可以对应 SBT 上某一层的一对相邻分数。考虑给出和上转化后的相同的生成方式。

　　考虑第 $k$ 层中一对存在对应关系的相邻分数 $(p, q)$。

　　如果 $p < q$，那么在树上的情况上是

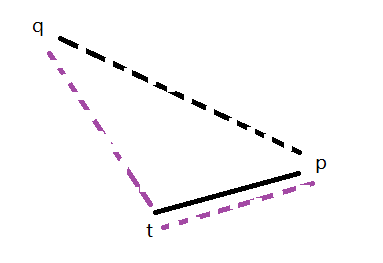
　　假设在 $p, q$ 间插入的分数为 $t$，根据 SBT 的构造方式可知 $q, t$ 是第 $(k + 1)$ 层的相邻分数 $t, p$ 是第 $(k + 1)$ 层的相邻分数。它们分别对应右加上左以及左加上右。当 $q < p$ 的时候是类似的。

　　对于一个真分数 $\frac{a}{b}$，$xa + yb$ 的值总是比相应的它生成的两个分数的 $x'a + y'b$ 小 。一对相邻分数一定满足一个是另一个的祖先，这个不难使用归纳法证明。

　　现在考虑加入 $m$ 的限制，那么真分数 $\frac{x}{y}$ 满足条件当且仅当 $x \leqslant y$ 以及 $xa + yb \leqslant m$，并且每一个满足条件的小于 $1$ 的真分数对应 $4$ 个满足条件的数对，特别地，1 如果合法只会对应 2 个满足条件的数对。

　　前一个条件是因为第一次只能大加上小，第二个是因为题目限制。充分性由 SBT 构造过程和上面转化给出。

　　那剩下的问题就非常傻逼了：

$$
\begin{align}
\sum_{i = 1}^{m} \sum_{j = 1}^{m} [i \leqslant j][(i, j) = 1][xi + yj \leqslant m]
\end{align}
$$

　　基础莫比乌斯反演 & 类欧几里得即可计算。

Code

#include <bits/stdc++.h>
using namespace std;
typedef bool boolean;

#define ll long long

ll ceil(ll a, ll b) {
	return (a < 0) ? ((a - b + 1) / b) : (a / b);
}

ll calc(ll a, ll b, ll c, ll n) {
	if (!n) {
		return 0;
	}
	if (!a) {
		return ceil(b, c) * n;
	}
	if (b < 0 || b >= c || a < 0 || a >= c) {
		ll ka = ceil(a, c), kb = ceil(b, c);
		ll tmp = ka * ((n * (n - 1)) >> 1) + kb * n;
		return calc(a - ka * c, b - kb * c, c, n) + tmp;
	}
	ll m = ((n - 1) * a + b) / c;
	return n * m - calc(c, c - b + a - 1, a, m);
}

const int C = 1e6 + 5;
const int D = 4e4 + 5;

int pri[C];
int mu[C], smu[C];

void Euler(int n) {
	static bitset<C> vis;
	int num = 0;
	mu[1] = 1;
	for (int i = 2; i <= n; i++) {
		if (!vis.test(i)) {
			pri[num++] = i;
			mu[i] = -1;
		}
		for (int *p = pri, *_ = pri + num, x; p != _ && (x = *p * i) <= n; p++) {
			vis.set(x);
			if (i % *p) {
				mu[x] = -mu[i];
			} else{
				mu[x] = 0;
				break;
			}
		}
	}
	for (int i = 1; i <= n; i++)
		smu[i] = smu[i - 1] + mu[i];
}

int T, N;

int smu1[D];
boolean vis[D];
int S(int n) {
	if (n <= 1000000)
		return smu[n];
	if (vis[N / n])
		return smu1[N / n];
	int &rt = smu1[N / n];
	rt = 1;
	vis[N / n] = true;
	for (int i = 2, j; i <= n; i = j + 1) {
		j = n / (n / i);
		rt -= S(n / i) * (j - i + 1);
	}
	return rt;
}

int main() {
	scanf("%d%d", &T, &N);
	Euler(1000000);
	int x, y;
	while (T--) {
		scanf("%d%d", &x, &y);
		if (x <= y) {
			puts("1");
			continue;
		}
		ll ans = 0;
		for (int i = 1, j; i <= N / (x + y); i = j + 1) {
			j = N / (N / i);
			ans += (S(j) - S(i - 1)) * calc(-x - y, N / i - x - y, x, N / (i * (x + y)));
		}
		ans = ((ans << 1) + 1 + (x + y <= N)) << 1;
		printf("%lld\n", ans);
	}
	return 0;
}