[LeetCode] 894. All Possible Full Binary Trees 所有可能的满二叉树

A *full binary tree* is a binary tree where each node has exactly 0 or 2 children.

Return a list of all possible full binary trees with Nnodes.  Each element of the answer is the root node of one possible tree.

Each node of each tree in the answer must have node.val = 0.

You may return the final list of trees in any order.

Example 1:

Input: 7
Output: [[0,0,0,null,null,0,0,null,null,0,0],[0,0,0,null,null,0,0,0,0],[0,0,0,0,0,0,0],[0,0,0,0,0,null,null,null,null,0,0],[0,0,0,0,0,null,null,0,0]]
Explanation:

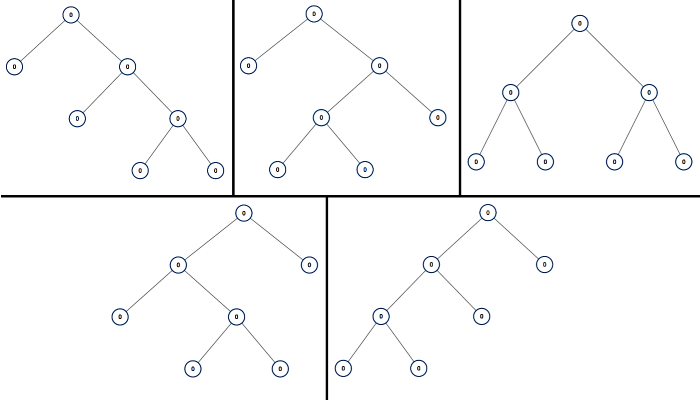
Note:

• 1 <= N <= 20

这道题给了一个数字N，让我们生成所有包含N个结点的满二叉树。所谓的满二叉树，就是每个结点一定会有0个或2两个子结点，换句话说，子结点必须成对出现，注意跟完全二叉树区分。现在我们有N个结点可以使用，若我们仔细观察，可以发现，所有的满二叉树的结点总数都是奇数，所以只要当N为偶数的时候，一定返回的是空数组，这个可以当作一个剪枝放在开头。下面我们就来考虑当N是奇数时，如何生成不同的满二叉树。先从最简单的开始，当 N=1 时，就只有一个根结点，当 N=3 时，也只有一种情况，根结点和左右子结点，当 N=5 时，就有如下两种情况：

    0
   / \
  0   0
 / \
0   0

    0
   / \
  0   0
     / \
    0   0

我们可以看出来就是在 N=3 的情况下再多加两个结点，这两个结点可以都在左子结点下，或者都在右子结点下。但是当 N=7 的时候就比较 tricky 了，也可以看作是在 N=5 的情况下生成的，我们可以把多余出来的两个结点分别加到上面两棵树的任意一个叶结点下方，但可能你会有疑问，上面的两棵树各自都有三个叶结点，每个都加的话，不就应该有6种情况了么，其实只有5种，因为其中有两种情况是重合的，即在第一棵树的最右叶结点下添加，跟在第二棵树的最左叶结点下添加后得到的完全二叉树是一样的，所以总共只有5种组合。

讲到这里，身为读者的你可能还是比较迷茫，到底该如何用代码来生成，我们再换一种思维方式，若总共有N个结点可以分配，那么除去根结点，左右子树一共可以分配 N-1 个结点，由于N一定是奇数，那么 N-1 一定就是偶数，所以左右子树需要共同来分配这 N-1 个结点。又因为满二叉树的子树也必须是满二叉树，所以每个子树的结点总数也应该是奇数，由于 N-1 是偶数，所以这 N-1 个结点不可能全部给其中的一个子树，即左右子树至少有一个结点，那么实际上就是把 N-1 这个偶数拆分成任意两个奇数之和，比如p和q，满足 p+q = N-1，且p，q均为奇数，然后对其分别对p和q调用递归函数，得到两个数组，数组里面的就是所有可能情况的左右子树的根结点。之后要做的就是从这两个数组中任意取两个结点，加到一个新建的 cur 结点的左右子结点上，然后将 cur 结点存入结果 res 中。这种处理方法跟之前的那两道题 Unique Binary Search Trees II，Different Ways to Add Parentheses 一模一样，若大家眼睛够尖的话，可以看出来这其实也是 卡塔兰数 Catalan Numbe，参见代码如下：

解法一：

class Solution {
public:
    vector<TreeNode*> allPossibleFBT(int N) {
        if (N % 2 == 0) return {};
        if (N == 1) return {new TreeNode(0)};
        vector<TreeNode*> res;
        for (int i = 1; i < N; i += 2) {
        	vector<TreeNode*> left = allPossibleFBT(i), right = allPossibleFBT(N - i - 1);
        	for (auto a : left) {
        		for (auto b : right) {
        			TreeNode *cur = new TreeNode(0);
        			cur->left = a;
        			cur->right = b;
        			res.push_back(cur);
        		}
        	}
        }
        return res;
    }
};

我们可以通过使用一个 HashMap 来避免重复计算，从而提升运算速度，建立每个值跟其对应的满二叉树的根结点数组之间的映射，那么在递归函数中，判定完了偶数跟1的情况后，就看当前N值是否已经计算过了，是的话，直接从 HashMap 中取数组，否则就进行和上面一样的运算，最后在返回前要将结果存入 HashMap 中，参见代码如下：


解法二：

class Solution {
public:
    unordered_map<int, vector<TreeNode*>> m;
    vector<TreeNode*> allPossibleFBT(int N) {
        if (N % 2 == 0) return {};
        if (N == 1) return {new TreeNode(0)};
        if (m.count(N)) return m[N];
        vector<TreeNode*> res;
        for (int i = 1; i < N; i += 2) {
        	vector<TreeNode*> left = allPossibleFBT(i), right = allPossibleFBT(N - i - 1);
        	for (auto a : left) {
        		for (auto b : right) {
        			TreeNode *cur = new TreeNode(0);
        			cur->left = a;
        			cur->right = b;
        			res.push_back(cur);
        		}
        	}
        }
        return m[N] = res;
    }
};

Github 同步地址:

https://github.com/grandyang/leetcode/issues/894

类似题目：

Unique Binary Search Trees II

Different Ways to Add Parentheses

参考资料：

https://leetcode.com/problems/all-possible-full-binary-trees/

[LeetCode All in One 题目讲解汇总(持续更新中...)](https://www.cnblogs.com/grandyang/p/4606334.html)