B+树比B树更适合实际应用中操作系统的文件索引和数据库索引

B+树比B树更适合实际应用中操作系统的文件索引和数据库索引

为什么选择B+树作为数据库索引结构？

 

背景

首先，来谈谈B树。为什么要使用B树？我们需要明白以下两个事实：

【事实1】
不同容量的存储器，访问速度差异悬殊。以磁盘和内存为例，访问磁盘的时间大概是ms级的，访问内存的时间大概是ns级的。有个形象的比喻，若一次内存访问需要1秒，则一次外存访问需要1天。所以，现在的存储系统，都是分级组织的。最常用的数据尽可能放在更高层、更小的存储器中，只有在当前层找不到，才向更低层、更大的存储器中寻找。这也就解释了，当处理大规模数据的时候（指无法将数据一次性存入内存），算法的实际运行时间，往往取决于数据在不同存储级别之间的IO次数。因此，要想提升速度，关键在于减少IO。

【事实2】
磁盘读取数据是以数据块(block)（或者：页，page）为基本单位的，位于同一数据块中的所有数据都能被一次性全部读取出来。换句话说，从磁盘中读1B，与读1KB几乎一样快！因此，想要提升速度，应该利用外存批量访问的特点，在一些文章中，也称其为磁盘预读。系统之所以这么设计，是基于一个著名的局部性原理：

当一个数据被用到时，其附近的数据也通常会马上被使用，程序运行期间所需要的数据通常比较集中

B树

假设有10亿条记录（1000*1000*1000），如果使用平衡二叉搜索树（Balanced Binary Search Tree, BBST），最坏的情况下，查找需要log(2, 10^9) = 30次 I/O 操作，且每次只能读出一个关键字（即如果这次读出来的关键字不是我要查找的，就要再进行一次I/O去读取数据）。如果换成B树，会是怎样的情况呢？

B 树是为了磁盘或其它辅助存储设备而设计的一种多叉平衡搜索树。多级存储系统中使用B树，可针对外部查找，大大减少I/O次数。通过B树，可充分利用外存对批量访问的高效支持，将此特点转化为优点。每下降一层，都以超级结点为单位（超级结点就是指一个结点内包含多个关键字），从磁盘中读入一组关键字。那么，具体多大为一组呢？

一个节点存放多少数据视磁盘的数据块大小而定，比如磁盘中1 block的大小有1024KB，假设每个关键字的大小为 4 Byte，则可设定每一组的大小m = 1024 KB / 4 Byte = 256。目前，多数数据库系统采用 m = 200~300。假设取m = 256，则B树存储1亿条数据的树的高度大概是 log(256, 10^9) = 4，也就是单次查询所需要进行的I/O次数不超过 4 次，由此大大减少了I/O次数。

一般来说，B树的根节点常驻于内存中，B树的查找过程是这样的：首先，由于一个节点内包含多个（比如，是256个）关键码，所以需要先顺序/二分来查找，如果找到则查找成功；如果失败，则根据相应的引用从磁盘中读入下一层的节点数据（这里就涉及到一次磁盘I/O），同样的在节点内顺序查找，如此往复进行...事实上，B树查找所消耗的时间很大一部分花在了I/O上，所以减少I/O次数是非常重要的。

B树的定义

B树就是平衡的多路搜索树，所谓的m阶B树，即m路平衡搜索树。根据维基百科的定义，一棵m阶B树需满足以下要求：

1. 每个结点至多含有m个分支节点（m>=2）。
2. 除根结点之外的每个非叶结点，至少含有┌m/2┐个分支。
3. 若根结点不是叶子结点，则至少有2个孩子。
4. 一个含有k个孩子的非叶结点包含k-1个关键字。 （每个结点内的关键字按升序排列）
5. 所有的叶子结点都出现在同一层。实际上这些结点并不存在，可以看作是外部结点。

根据节点的分支的上下限，也可以称其为(┌m/2┐, m)树。比如，阶数m=4时，这样的B树也可以称为(2,4)树。（事实上，(2,4)树是一棵比较特殊的B树，它和红黑树有着特别的渊源！后面谈及红黑树时会谈到。）

并且，每个内部结点的关键字都作为其子树的分隔值。比如，某结点含有2个关键字（假设为a1和a2），也就是说该结点含有3个子树。那么，最左子树的关键字均小于a1；中间子树的关键字介于a1~a2；最右子树的关键字均大于a2。

示例，一棵3阶的B树是这个样子：

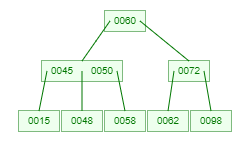
B树的高度（了解）

假定一棵B树非空，具有n个关键字、高度为h（令根结点为第1层）、阶数为m，那么该B树的最大高度和最小高度分别是多少？

最大高度

当树的高度最大时，则每个结点含有的关键字数应该尽量少。根据定义，根结点至少有2个孩子（即1个关键字），除根结点之外的非叶结点至少有┌m/2┐个孩子（即┌m/2┐-1个关键字），为了描述方便，这里令p = ┌m/2┐。

第1层 1个结点  （含1个关键字）
第2层 2个结点  （含2*(p-1)个关键字）
第3层 2p个结点 （含2p*(p-1)^2个关键字）
...
第h层 2p^(h-2)个结点

故总的结点个数n
≥ 1+(p-1)*[2+2p+2p^2+...+2p^(h-2)]
≥ 2p^(h-1)-1
从而推导出 h ≤ log_p[(n+1)/2] + 1 （其中p为底数，p=┌m/2┐）

最小高度

当树的高度最低时，则每个结点的关键字都至多含有m个孩子（即m-1个关键字），则有

n ≤ (m-1)*(1 + m + m^2 +...+ m^(h-1)) = m^h - 1
从而推导出 h ≥ log_m(n+1)  （其中m为底数）

B+树

B+树的定义

B+树是B树的一个变体，B+树与B树最大的区别在于：

1. 叶子结点包含全部关键字以及指向相应记录的指针，而且叶结点中的关键字按大小顺序排列，相邻叶结点用指针连接。
2. 非叶结点仅存储其子树的最大（或最小）关键字，可以看成是索引。

一棵3阶的B+树示例：（好好体会和B树的区别，两者的关键字是一样的）

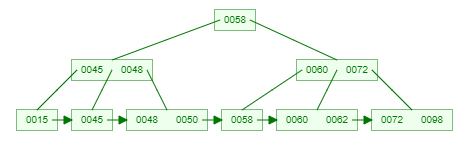
问：为什么说B+树比B树更适合实际应用中操作系统的文件索引和数据库索引？

答：

1. B+树更适合外部存储。由于内结点不存放真正的数据（只是存放其子树的最大或最小的关键字，作为索引），一个结点可以存储更多的关键字，每个结点能索引的范围更大更精确，也意味着B+树单次磁盘IO的信息量大于B树，I/O的次数相对减少。
2. MySQL是一种关系型数据库，区间访问是常见的一种情况，B+树叶结点增加的链指针，加强了区间访问性，可使用在区间查询的场景；而使用B树则无法进行区间查找。

---

参考：
1）清华大学邓俊辉数据结构-高级搜索树
2）https://www.cs.usfca.edu/~galles/visualization/BPlusTree.html （数据结构可视化）