二维离散余弦变换（2D-DCT）

图像处理中常用的正交变换除了傅里叶变换以外，还有一些其它常用的正交变换，其中离散余弦变换DCT就是一种，这是JPEG图像压缩算法里的核心算法，这里我们也主要讲解JPEG压缩算法里所使用8*8矩阵的二维离散余弦正变换。

一维离散余弦变换

一般表达式

要弄懂二维离散余弦变换，首先我们需要先了解它在一维下的情况，具体表达式如下：

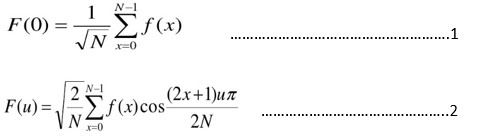
式中F(u)是第u个余弦变换值，u是广义频率变量，u=1,2,….,N-1;f(x)是时域N点序列。x= 1,2,….,N-1;

矩阵表示法

更为简洁的定义离散余弦变换是采用矩阵式定义。根据以上公式定义可知，我们可以来推导一下，DCT变换可以用矩阵的形式表示出来，例当N=8时一维离散余弦变换的表达式展开可以得到如下表达式： u=1,2,...7

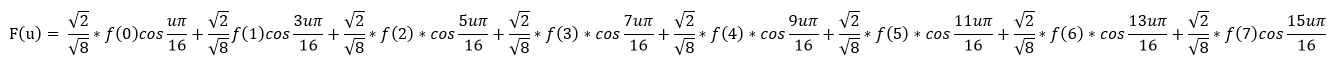
当u=0,1，...，7时，我们可以根据上述公式计算出离散余弦变换时每一个f(x)前面的变换系数如下：

上式可以用矩阵的形式表达出来

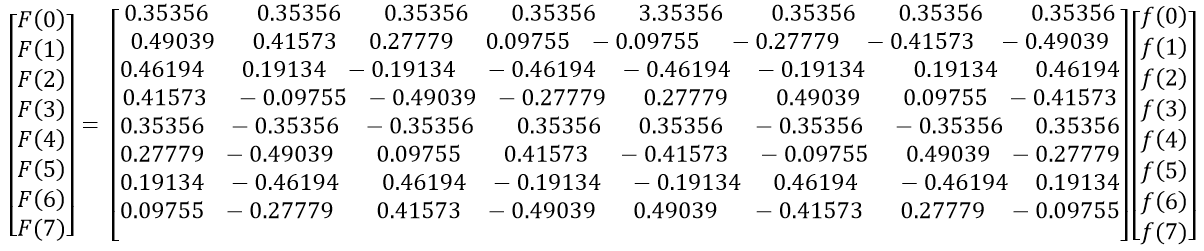
F(u)为变换域矩阵，是时域f(x)与A矩阵计算的结果；A为变换系数矩阵,当N取定值时，A就是一个常量矩阵；f(x)为时域数据矩阵，即需要转换到变换域的原始数据，则一维离散余弦变换的矩阵定义式可写成下方表达式：

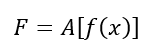
二维离散余弦变换

二维离散余弦变换可由下列表达式表示

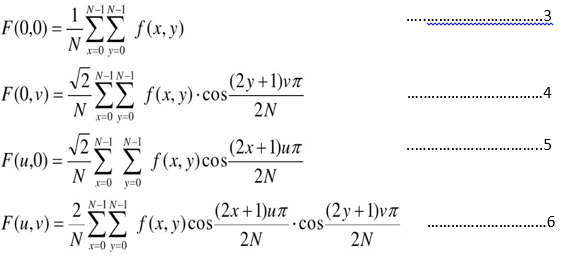
6是二维离散余弦变换的正变换公式，其中f(x,y)是空间域一个N*N的二维向量元素，即一个N*N的矩阵，x,y = 0,1,2，…，N-1;F(U,V)是经计算后得到的变换域矩阵，u,v = 0,1,2，….，N-1.求和可分性是二维离散余弦变换的一个重要特征，因此我们可以用下式表示6：

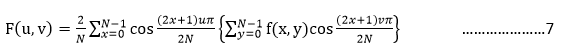
由一维和二维的离散余弦变换公式性质可以推导得到二维离散余弦变换也可以写成矩阵相乘形式

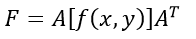
A为一维离散余弦变换的变换系数矩阵，A^T是A的转置矩阵

对图像进行二维离散余弦变换（2D-DCT）的步骤

1.获得图像的二维数据矩阵f(x,y)；

2.求离散余弦变换的系数矩阵A；

3.求系数矩阵对应的转置矩阵A^T；

4.根据公式F=A[f(x,y)]A^T计算离散余弦变换；