【Foreign】数据结构C [线段树]

数据结构C

Time Limit: 20 Sec  Memory Limit: 512 MB

Description

　　

Input

　　

Output

　　

Sample Input

　　

Sample Output

　　

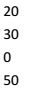
HINT

　　

Solution

　　首先，D操作为删除操作显然不可做，又发现这道题可以离线处理，那么我们考虑倒着来，维护加入操作。

　　那么这时候，D操作就变为了合并操作，那么这时候我们只需要维护一个：可以支持单点修改、查询第 k 大、信息可合并的数据结构即可。

　　显然构建若干棵权值线段树即可！对于每个联通块维护一棵线段树，用并查集判断两点是否在一个块内。

　　这时候，D操作显然判断一下两点是否在一个联通块内，不在则合并两棵线段树；Q操作就是查询第 k 大，在树上二分即可；C操作就是原来值个数-1，新加入值个数+1。

　　就简单地解决了这题啦！（本质上就是BZOJ1926弱化 + BZOJ1015 QWQ）

Code

 #include<iostream>
 #include<algorithm>
 #include<cstdio>
 #include<cstring>
 #include<cstdlib>
 #include<cmath>
 using namespace std;

 const int ONE = ;
 const int INF = 2e6;
 const int Base = 1e6;

 int n, m;
 int opt, x, val;
 int Val[];
 char s[];

 int Ans[], ans_num = ;

 int fat[];

 int Num = , del[];
 struct power {int opt, x, val;} oper[ONE];
 struct point {int x, y;} a[];
 int total = ;
 struct seg
 {
         int root;
         int left, right;
         int val;
 }Node[ONE * ];

 int get()
 {
         int res=,Q=;    char c;
         while( (c=getchar())< || c>)
         if(c=='-')Q=-;
         if(Q) res=c-;
         while((c=getchar())>= && c<=)
         res=res*+c-;
         return res*Q;
 }

 int Find(int x)
 {
         if(fat[x] == x) return x;
         return fat[x] = Find(fat[x]);
 }

 void Un(int x, int y)
 {
         int f1 = Find(x), f2 = Find(y);
         if(f1 != f2) fat[f1] = f2;
 }

 void Update(int &i, int l, int r, int Val, int opt) //pos = Val , + opt
 {
         if(!i) i = ++total;

         Node[i].val = Node[i].val + opt;

         if(l == r) return;
         int mid = l + r >> ;

         if(Val <= mid) Update(Node[i].left, l, mid, Val, opt);
         else Update(Node[i].right, mid + , r, Val, opt);

 }

 int Merge(int y, int x) //y merge to x
 {
         if(x ==  || y == ) return x + y;

         Node[x].val += Node[y].val;
         Node[x].left =  Merge(Node[x].left, Node[y].left);
         Node[x].right = Merge(Node[x].right, Node[y].right);

         return x;
 }

 int Query(int i, int l, int r, int k) //k da
 {
         if(l == r) return l;
         int mid = l + r >> , Val = Node[ Node[i].right ].val;

         if(k > Val)
             return Query(Node[i].left, l, mid, k - Val);
         else
             return Query(Node[i].right, mid + , r, k);
 }

 void Deal_first()
 {
         for(int i = ; i <= n; i++)
             fat[i] = i, Node[i].root = ++total;
         for(int i = ; i <= m; i++)
             if(del[i] != ) Un(a[i].x, a[i].y);
         for(int i = ; i <= n; i++)
             Update(Node[Find(i)].root, , INF, Val[i], );
 }

 void Deal_add(int x, int y)
 {
         x = Find(x), y = Find(y);
         if(x == y) return;
         Merge(Node[x].root, Node[y].root);
         fat[x] = y;
 }

 void Deal_query(int root, int k)
 {
         root = Find(root);
         if(Node[root].val < k) {Ans[++ans_num] =  + Base; return;}
         Ans[++ans_num] = Query(Node[root].root, , INF, k);
 }

 void Deal_change(int x, int y) //x is point, y is need val
 {
         int root = Find(x);
         Update(Node[root].root, , INF, Val[x], -);
         Update(Node[root].root, , INF, y, );
         Val[x] = y;
 }

 int main()
 {
         n = get();    m = get();

         for(int i = ; i <= n; i++) Val[i] = get() + Base;
         for(int i = ; i <= m; i++)
             a[i].x = get(), a[i].y = get();
         for(;;)
         {
             scanf("%s", s);
             if(s[] == 'E') break;
             if(s[] == 'D')
                 x = get(), del[x] = , oper[++Num] = (power){, x, };
             if(s[] == 'Q')
                 x = get(), val = get(), oper[++Num] = (power){, x, val};
             if(s[] == 'C')
                 x = get(), val = get(), oper[++Num] = (power){, x, Val[x]}, Val[x] = val + Base;
         }

         Deal_first();
         for(int i = Num; i >= ; i--)
         {
             if(oper[i].opt == ) Deal_add(a[ oper[i].x ].x, a[ oper[i].x ].y);
             if(oper[i].opt == ) Deal_query(oper[i].x, oper[i].val);
             if(oper[i].opt == ) Deal_change(oper[i].x, oper[i].val);
         }

         for(int i = ans_num; i >= ; i--)
             printf("%d\n", Ans[i] - Base);
 }

• [提交][状态][讨论]