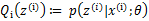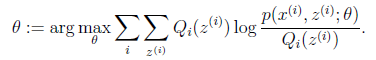Expectation Maximization（EM）算法note

　　EM算法，之前上模式识别课上，推导过，在《统计学习方法》中没耐性的看过几次，个人感觉讲的过于理论，当时没怎么看懂，后来学lda，想要自己实现一下em算法，又忘记了，看来还是学的不够仔细，认识的不够深刻，现在做点笔记。本文是看了几篇blog和《统计学习方法》之后做的笔记，只是用来给自己做记录，很多地方都是直接引用。

一、初识

1. 迭代

　　EM算法本身可以理解为一个迭代算法，很抽象&简单的形容迭代就是，比如我们有两个公式a=f(b), b=g(a)，需要求解，我们可以先随机的给a赋一个值，在根据b=g(a)计算出b，得到b，在根据b得到a，如此往复，直到a，b基本不变。

2. 隐变量问题

　　EM算法很适用与求解包含隐变量的问题，这里引用《统计学习方法》中的一个例子（pLSA的弱化版本）：

　　eg. 有3枚硬币，分别记为A，B，C，掷得正面的概率分别为∏，p，q；
　　　　先投掷硬币A，如果是正面则继续投掷硬币B，是反面则投掷硬币C，最终出现正面记为1，出现反面记为0；
　　　　独立的重复n次实验后，得到一串实验结果Y=(Y1,Y2,……,Yn)。

　　这里Y=(Y₁,Y₂,……,Y_n)^T称作观测变量，但这里也有不能直接观测到，但却需要知道的一个变量，即投掷A的结果，可以记为Z=(Z₁,Z₂,……,Z_n)^T，同时有些已知的参数，我们可以统一记为θ=(∏, p, q)。通过上面的一些符号，我们可以得知Y的分布：

　　上式即为Y的似然函数，得到了似然函数，第一想到的便是参数的似然估计 ，下面回顾一下最大似然估计（MLE）的一般步骤：

求最大似然函数估计值的一般步骤：
（）写出似然函数；
（）对似然函数取对数，并整理；
（）求导数，令导数为0，得到似然方程；
（）解似然方程，得到的参数即为所求

其实最大似然可以这样想，我们假设已经知道到了θ，在已知θ的情况下，产生Y，很自然，如果我们看到结果产生了很多个Yi，那么P(Yi|θ)一定是比较大的。现在我们反过来想，我们已经知道了Y，

，那么使该结果出现的可能性最大的参数情况，就是我们估计的参数。

　　很不巧，上述步骤，是没有解析解的，这样我们就必须用到EM算法了。

（ps，这里有一篇对常见的三类估计介绍写的不错的文章文本语言模型的参数估计-最大似然估计、MAP及贝叶斯估计）

3. Jensen不等式

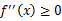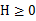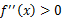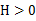回顾优化理论中的一些概念。设f是定义域为实数的函数，如果对于所有的实数x，，那么f是凸函数。当x是向量时，如果其hessian矩阵H是半正定的（），那么f是凸函数。如果或者，那么称f是严格凸函数。

Jensen不等式表述如下：

　　  如果f是凸函数，X是随机变量，那么

　　 　　　　 

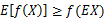
　　    特别地，如果f是严格凸函数，那么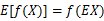当且仅当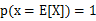，也就是说X是常量。

如果用图表示会很清晰：

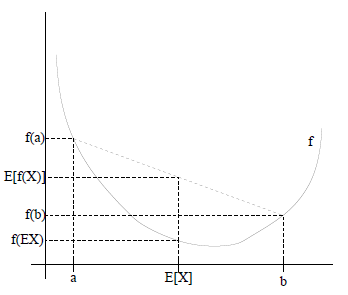
图中，实线f是凸函数，X是随机变量，有0.5的概率是a，有0.5的概率是b。（就像掷硬币一样）。X的期望值就是a和b的中值了，图中可以看到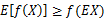成立。

当f是（严格）凹函数当且仅当-f是（严格）凸函数。

Jensen不等式应用于凹函数时，不等号方向反向，也就是。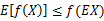

二、EM算法

　　上面的例子，有个很悬乎的变量，我们无法直接知道，即A硬币的投掷结果，但如果我们知道了某一次输出在投掷A后的输出是什么了，我们就能够很容易运用最大似然（当然，这个例子用简单的直觉也能知道）得到p，q的估计值。

eg.
　　.如果A硬币的投掷结果有x次正面，n-x次反面（在这个假设下，也就得到了∏的估计值），那么我们只要统计那x次中最后出现的正反面情况就能得到p的估计值了，对q也同理；
　　.得到了p，q值之后，我们又容易反过来问，你怎么知道之前的假设是正确的呢？而在已知p，q的情况下，之前我们的似然函数就能够求解了，这样我们就又能得到一个新的∏
　　.在新的∏值下，我们又可以对p，q进行新的估计了。如此往复，如果最终收敛了，那么就得到了我们对参数θ的估计值

　　上面说的很抽象，下面具体地说一说（以下部分引自（EM算法）The EM Algorithm）。

　　给定的训练样本是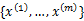，样例间独立，那么样本的似然函数如下：

　　   

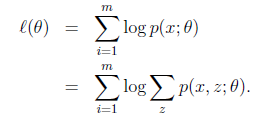
第一步是对极大似然取对数，第二步是对每个样例的每个可能类别z求联合分布概率和（对z求和后即可得到x的边缘分布概率）。但是直接求θ一般比较困难，因为有隐藏变量z存在，但是一般确定了z后，求解就容易了。

EM是一种解决存在隐含变量优化问题的有效方法。竟然不能直接最大化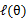，我们可以不断地建立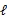的下界（E步），然后优化下界（M步）。这句话比较抽象，看下面的。

对于每一个样例i，让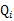表示该样例隐含变量z的某种分布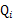，满足的条件是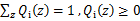。（如果z是连续性的，那么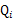是概率密度函数，需要将求和符号换做积分符号）。比如要将班上学生聚类，假设隐藏变量z是身高，那么就是连续的高斯分布。如果按照隐藏变量是男女，那么就是伯努利分布了（上文提到的三个硬币的例子中的∏就可以理解为这里的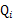，对于每个i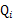，都是∏，∏是伯努利分布）。

　　可以由前面阐述的内容得到下面的公式：

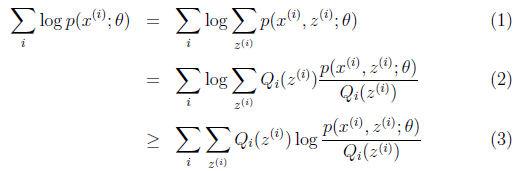
（1）到（2）比较直接，就是分子分母同乘以一个相等的函数。

（2）到（3）利用了Jensen不等式。

　　考虑到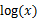是凹函数（二阶导数小于0），而且 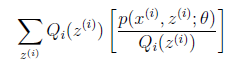 ，可以理解为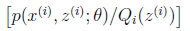的期望。得到(3)式后，我可以理解为，得到了似然函数l(θ)的一个下界，如果不断提升下界，使下界的值与l(θ)近似相等时，我们就可以用不等式右边的值代替l(θ)了。

　　对于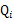的选择，有多种可能，那种更好的？假设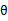已经给定，那么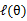的值就决定于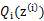和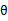（其实应该是，但这里只有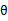未知）。首先我们思考当和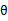都已经确定时，也就是jensen不等式中的随机变量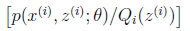已知时，我们可以知道当该随机变量恒为常数时，不等式取等号，即：

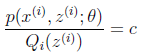
c为常数，不依赖于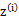（但确是依赖于x⁽ⁱ⁾的，所以对于不同i，c还是不一样的，但都是常数，所以在M步中不能恒为c）。对此式子做进一步推导，我们知道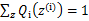，那么也就有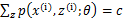，那么有下式：

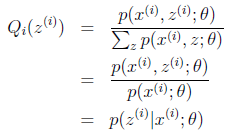
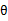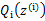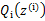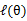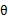至此，我们推出了在固定其他参数后，的计算公式就是后验概率，解决了如何选择的问题。这一步就是E步，建立的下界。接下来的M步，就是在给定后，调整，去极大化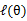的下界（在固定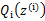后，下界还可以调整的更大）。那么一般的EM算法的步骤如下：

循环重复直到收敛 {

（E步）对于每一个i，计算

（M步）计算

　这里需要说明几点，比如，从第(t)步到(t+1)步：E步是固定θ^(t)，得到了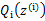，那么在M步中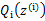，中的θ将还是上一步的θ^(t)，而P(x⁽ⁱ⁾,z⁽ⁱ⁾;θ)则是需要求解的θ，改变该θ的值，去使M步中式子的值最大的时刻对应的θ，即为新的θ^(t+1)所以M步中的式子可以进一步优化成

　　　　

因为都是求max时对应的θ，所以分母上的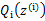可以不用计算了，而这一步就是最大化似然函数的期望。

　　Zhai老师在一篇经典的EM算法Notes中讲到，当原始数据的似然函数很复杂时，我们通过增加一些隐含变量来增强我们的数据，得到“complete data”,而“complete data”的似然函数更加简单，方便求极大值。于是，原始的数据就成了“incomplete data”。我们将会看到，我们可以通过最大化“complete data”似然函数的期望来最大化"incomplete data"的似然函数，以便得到求似然函数最大值更为简单的计算途径。

　　那么如何证明EM算法会收敛，其实有下面公式就好了：

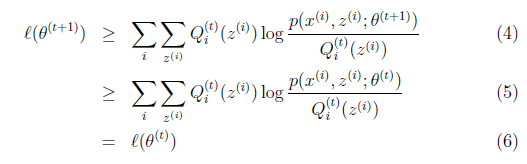
这里证明了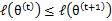，即l(θ)是单调上升的，到最后就一定能收敛到最大值。具体解释：

（4）是对所有的参数都满足，而其等式成立条件只是在固定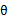，并调整好Q时成立（即如果是，等式成立），这里不一定等于，所以不一定能取等号。

（4）到（5）就是M步的定义，是固定第t步，固定Q调整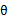得到的结果

（5）到（6）是前面E步所保证等式成立条件。

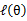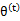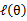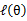　　也就是说E步会将下界拉到与一个特定值（这里）一样的高度，而此时发现下界仍然可以上升，因此经过M步后，下界又被拉升，但达不到与另外一个特定值一样的高度，即此时下界还是要小于，之后E步又将下界拉到与这个特定值一样的高度，重复下去，直到将下界拉升到的最大值。

　　某 blog 中有个很形象的图，引用到这里

　　　　

如果定义

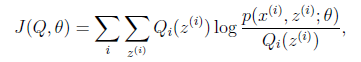
从前面的推导中我们知道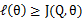，EM可以看作是J的坐标上升法，E步固定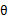，优化，M步固定优化。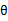

EM算法的基本原理就是这些了

Reference

1. 统计学习方法

2. http://www.cnblogs.com/jerrylead/archive/2011/04/06/2006936.html

3. http://blog.csdn.net/zouxy09/article/details/8537620

4. Andrew Ng 课程

5. http://blog.csdn.net/yangliuy/article/details/8330640