Folyd + 路径存储

一、Folyd 算法原理

　　

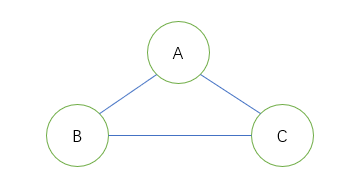
1. 如果 AB + AC < BC 那么， BC最短路就要经过 A。 在算法进行过程中，应该是 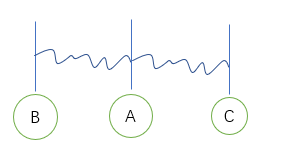，B-A 有很多路径，B 代表这些路径权值之和，A-C也有很多路径，C是这些权值之和。那么我们找到一个 满足  AB + AC < BC 的时候更新权值数组，并且记录路径。

2. dist[i][j] = k 表示，从 I -- J 点的路径权值为 K

3. 记录路径，就是将 C 点连接在 B A C 这样的路径后  

二、简单容易理解版

核心代码：

 //邻接矩阵保存点信息
 int mapp[MAX_POINT][MAX_POINT];
 //保存任意两点之间的最短路径上的节点
 vector<int> trace_path[MAX_POINT][MAX_POINT];

 void Folyd(int n) {
     for (int k = ; k < n; k++)
         for (int i = ; i < n; i++)
             for (int j = ; j < n; j++)
                 if (mapp[i][j] > mapp[i][k] + mapp[k][j]) {
                     mapp[i][j] = mapp[i][k] + mapp[k][j];
                     trace_path[i][j].clear();
                     //放入 i---k 路径节点
                     for (int z = ; z < trace_path[i][k].size(); z++)
                         trace_path[i][j].push_back(trace_path[i][k][z]);
                     //放入 k---j 路径节点
                     for (int z = ; z < trace_path[k][j].size(); z++)
                         trace_path[i][j].push_back(trace_path[k][j][z]);
                 }
 }

 void query(int from, int to) {
     cout << "from " << from << " to " << to << " should cost " << mapp[from][to] <<"."<< endl;
     cout << "trace_path: " ;
     for (int i = ; i < trace_path[from][to].size(); i++)
         cout<< trace_path[from][to][i] << " -> ";
     cout << to << endl;
 }

上述代码中：存在重复存储，效率极低

 trace_path[i][j].clear();
 //放入 i---k 路径节点
 for (int z = ; z < trace_path[i][k].size(); z++)
     trace_path[i][j].push_back(trace_path[i][k][z]);
 //放入 k---j 路径节点
 for (int z = ; z < trace_path[k][j].size(); z++)
     trace_path[i][j].push_back(trace_path[k][j][z]);

优化代码：

由于上面代码每次都重复把点的信息都保存下来，因此，我们采用保存前驱几点的方式，最终通过回溯构建路径。

path[i][j] = k ; //表示 从 i---j 路径中， k 是 j 的直接前驱， 那么最短路径 1->5->4->3->6 有 paht[1][6] = 3; paht[1][3]= 4; paht[1][4] = 5; paht[1][5] =1 如此逆推不难得到 最短路径记录值

核心代码：

 //邻接矩阵保存点信息
 int mapp[MAX_POINT][MAX_POINT];
 //path[i][j] = k ,表示从 i 到 j 最短路， k 邻接到j。
 int path[MAX_POINT][MAX_POINT];
 void Folyd(int n) {
     //初始化路径数组
     for (int i = ; i < n; i++)
         for (int j = ; j < n; j++) {
             if (mapp[i][j] - INF)
                 path[i][j] = i;
             else
                 path[i][j] = NOTEXISTS;
         }

     for (int k = ; k < n; k++)
         for (int i = ; i < n; i++)
             for (int j = ; j < n; j++)
                 if (mapp[i][j] > mapp[i][k] + mapp[k][j]) {
                     mapp[i][j] = mapp[i][k] + mapp[k][j];
                     //path[i][j] = k; //这种思路中，不能写成这样
                     path[i][j] = path[k][j];
                 }
 }

 void print_path(int from, int to) {
     if (path[from][to] != from)
         print_path(from, path[from][to]);
     cout << " -> " << to;
 }

在更改权值的时候，即使记录下来当前点的前驱节点。 path[i][j] = path[k][j]; 切不可以写成，path[i][j] = k;  后者是另一种思路，下面会描述。path[i][j] = path[k][j] 达到 j 节点 的前驱节点修改为经过k到j的路径上去。

完整代码：

测试数据：

 -  

1. 基础版本

 //Folyd
 #include <iostream>
 #include <vector>
 #include <algorithm>

 using namespace std;

 const int INF = 0x3f3f3f3f;
 const int MAX_POINT = ;

 //邻接矩阵保存点信息
 int mapp[MAX_POINT][MAX_POINT];
 //保存任意两点之间的最短路径上的节点
 vector<int> trace_path[MAX_POINT][MAX_POINT];

 void Folyd(int n) {
     for (int k = ; k < n; k++)
         for (int i = ; i < n; i++)
             for (int j = ; j < n; j++)
                 if (mapp[i][j] > mapp[i][k] + mapp[k][j]) {
                     mapp[i][j] = mapp[i][k] + mapp[k][j];
                     trace_path[i][j].clear();
                     //放入 i---k 路径节点
                     for (int z = ; z < trace_path[i][k].size(); z++)
                         trace_path[i][j].push_back(trace_path[i][k][z]);
                     //放入 k---j 路径节点
                     for (int z = ; z < trace_path[k][j].size(); z++)
                         trace_path[i][j].push_back(trace_path[k][j][z]);
                 }
 }

 void query(int from, int to) {
     cout << "from " << from << " to " << to << " should cost " << mapp[from][to] <<"."<< endl;
     cout << "trace_path: " ;
     for (int i = ; i < trace_path[from][to].size(); i++)
         cout<< trace_path[from][to][i] << " -> ";
     cout << to << endl;
 }

 int main(int argc, char const *argv[])
 {
     int n;
     cout << "Please input gragh points:";
     cin >> n;
     //init container， 自己到自己默认 0，其他为 INF
     for (int i = ; i < n; i++) {
         mapp[i][i] = ;
         for (int j = ; j < n; j++)
             if (i != j)
                 mapp[i][j] = INF;
     }

     int t = (n*(n - )) >> ;
     // 最多输入 n(n -1)>>1 条边
     cout << "Please input edges format a tuple (f, t , v), to end input via (-1, 0, 0)" << endl;
     while (--t > ) {
         int from, to, value;
         cin >> from >> to >> value;
         if (~from) {
             //无向图
             mapp[from][to] = value;
             mapp[to][from] = value;
             //每条路的前驱放入路径中
             trace_path[from][to].push_back(from);
             trace_path[to][from].push_back(to);
         }
         else
             break;
     }

     Folyd(n);

     //结果打表
     cout << "====================" << endl;
     for (int i = ; i < n; i++) {

         for (int j = ; j < n; j++)
             cout << mapp[i][j] << "\t";
         cout << endl;
     }
     cout << "====================" << endl;
      while(){
          int beginP, endP;
          cout << "Please input begin point and end point:";
          cin >> beginP >> endP;
          query(beginP, endP);
      }
     return ;
 }

2. 改进版本

 //Folyd
 //输入图,可以不连通
 #include <iostream>
 using namespace std;

 const int INF = 0x3f3f3f3f;
 const int MAX_POINT = ;
 const int NOTEXISTS = ~(0U);

 //邻接矩阵保存点信息
 int mapp[MAX_POINT][MAX_POINT];
 //path[i][j] = k ,表示从 i 到 j 最短路， k 邻接到j。
 int path[MAX_POINT][MAX_POINT];
 void Folyd(int n) {
     //初始化路径数组
     for (int i = ; i < n; i++)
         for (int j = ; j < n; j++) {
             if (mapp[i][j] - INF)
                 path[i][j] = i;
             else
                 path[i][j] = NOTEXISTS;
         }

     for (int k = ; k < n; k++)
         for (int i = ; i < n; i++)
             for (int j = ; j < n; j++)
                 if (mapp[i][j] > mapp[i][k] + mapp[k][j]) {
                     mapp[i][j] = mapp[i][k] + mapp[k][j];
                     path[i][j] = path[k][j];
                 }
 }

 void print_path(int from, int to) {
     if (path[from][to] != from)
         print_path(from, path[from][to]);
     cout << " -> " << to;
 }

 int main(int argc, char const *argv[])
 {
     int n;
     cout << "Please input gragh points:";
     cin >> n;

     //init container
     for (int i = ; i < n; i++) {
         mapp[i][i] = ; //自己到自己默认 0
         for (int j = ; j < n; j++)
             if (i != j)
                 mapp[i][j] = INF;
     }

     int t = (n*(n - )) >> ;
     // 最多输入 n(n -1)>>1 条边
     cout << "Please input edges format a tuple (f, t , v), to end input via (-1, 0, 0)" << endl;
     while (--t > ) {
         int from, to, value;
         cin >> from >> to >> value;
         if (~from) {
             mapp[from][to] = value;
             mapp[to][from] = value;
         }
         else
             break;
     }
     Folyd(n);

     cout << "====================" << endl;
     for (int i = ; i < n; i++) {

         for (int j = ; j < n; j++)
             cout << mapp[i][j] << "\t";
         cout << endl;
     }
     cout << "====================" << endl;
     while () {
         int beginP, endP;
         cout << "Please input begin point and end point:";
         cin >> beginP >> endP;
         //print path
         cout << "from " << beginP << " to " << endP << " should cost " << mapp[beginP][endP] << "." << endl;
         if (path[beginP][endP] == NOTEXISTS)
             cout << "No path!" << endl;
         else {
             cout << "trace_path: ";
             cout << beginP;
             print_path(beginP, endP);
             cout << endl;
         }
     }
     return ;
 }

参考资料：

https://blog.csdn.net/start0609/article/details/7779042

https://blog.csdn.net/immiao/article/details/22199939