最小角回归 LARS算法包的用法以及模型参数的选择（R语言）

Lasso回归模型，是常用线性回归的模型，当模型维度较高时，Lasso算法通过求解稀疏解对模型进行变量选择。Lars算法则提供了一种快速求解该模型的方法。Lars算法的基本原理有许多其他文章可以参考，这里不过多赘述, 这里主要简介如何在R中利用lars算法包求解线性回归问题以及参数的选择方法。

以下的的一些用法参照lars包的帮助文件，再加上自己的使用心得。所用的示例数据diabetes是Efron在其论文中“Least Angle Regression”中用到的，可以在加载lars包后直接获得

library(lars)
data(diabetes)
attach(diabetes)

该数据中含有三个变量x,x2,y, 其中x是一个有422X10维的矩阵，y是一422维个向量，x2是由x得到的 422X64维矩阵（compressive）.

1. 求解路径solution path

lars(x, y, type = c("lasso", "lar", "forward.stagewise", "stepwise"), trace = FALSE, normalize = TRUE, intercept = TRUE, Gram, eps = .Machine$double.eps, max.steps, use.Gram = TRUE)

该函数提供了通过回归变量x和因变量y求解其回归解路径的功能。其中，

type ---- 表示所使用的回归方法，包括（lasso, lar, forward.stagewise, stepwise），选择不同的回归方法将得到不同的解路径；

normalize ---- 表示是否对变量进行归一化，当为TRUE时，程序将对x和y进行L2正则化；

intercept ---- 表示是否对变量进行中心化，当为TRUE时，程序将对x和y分别减去其均值。

下面使用四种不同的回归方法对其进行回归分析

object1 <- lars(x,y,type="lasso")
object2 <- lars(x,y,type="lar")
object3 <- lars(x,y,type="forward.stagewise")
object4 <- lars(x,y,type="stepwise")

返回参数是一个list，其中包含了每次迭代得到的回归系数beta以及lambda等16个返回值。

可以分别对返回参数用plot( )画出其solution path的图像.

可以看到lars算法，算法的步数较少即迭代次数较少，且与参数个数相同，当数据维数非常高的时候lars算法相较于其他回归算法速度非常快。

2. 利用交叉验证(Cross Validtion)确认参数

在上一步我们可以看到lars一次给了其solution path上的所有解，我们需要确定其中哪个解是我们真正要用到的. 在lasso模型中，约束项由参数lambda进行控制，当给定了lambda，模型才能够确定下来。一个好的回归模型，需要给定一个合适的lambda，但是lamda的范围往往比较大。注意到www.255055.cn/ lars算法给出的解路径上的解个数是有限的，不同的解即不同的beta就对应了不同的lambda, 从solution path的图可以看到，我们可以通过选定算法的step步数或者选定beta饱和度|beta|/max|beta|（此处| |表示一范数，饱和度同样也表征了解的稀疏度）来选定模型的参数.

此时就需要用到lars包中的cv.lars函数，

cv.lars(x, y, K = 10, index, trace = FALSE, plot.it = TRUE, se = TRUE,type = c("lasso", "lar", "forward.stagewise", "stepwise"), mode=c("fraction", "step"), ...)

K ----- 表示在进行交叉验证时，将数据随机分为K份，每次使用其中K-1份作为训练数据，用剩下的一份进行验证，最后计算这K次验证的均方误差;

mode ----- 表示用到的参数指标， step即按步数step去选择所需的参数，fraction即按照path中的横坐标|beta|/max|beta|去选择所需变量，fraction默认为0：100：1即 index=seq(from=0,to=1,length=100).

其他的type等参数与lars()中的意义相同，下面我们以type="lar"时为例，以x2为自变量，演示确定回归参数的方法.

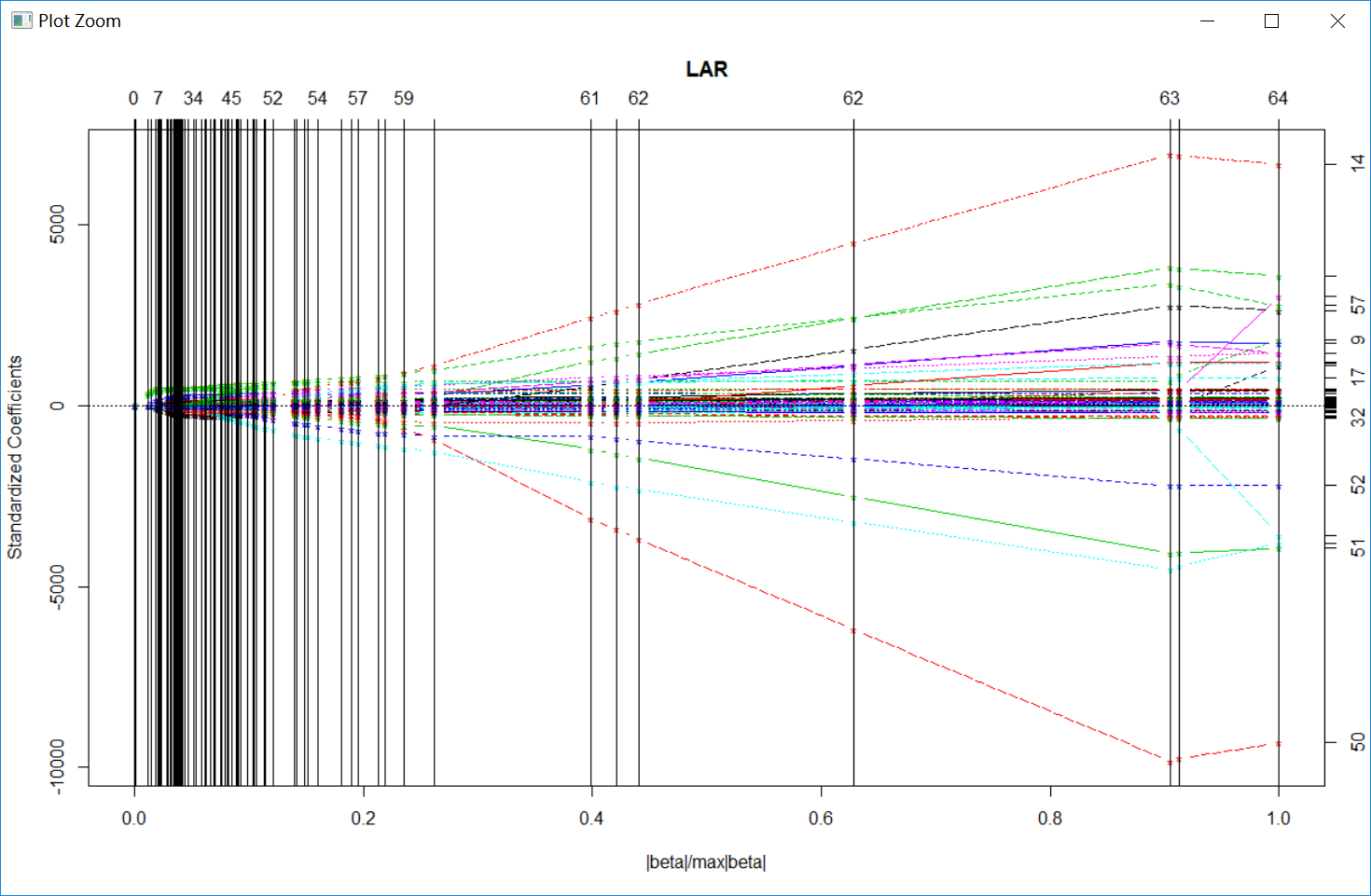
首先为方便描述，我们先单独画出使用该方法得到的solution path

然后利用lars.cv来确定其参数，首先使用的index为mode="www.huayi1.cn/ step"

data(diabetes)
attach(diabetes)
cvsol1<-cv.lars(x2,y,type="lar",mode="step")
detach(diabetes)

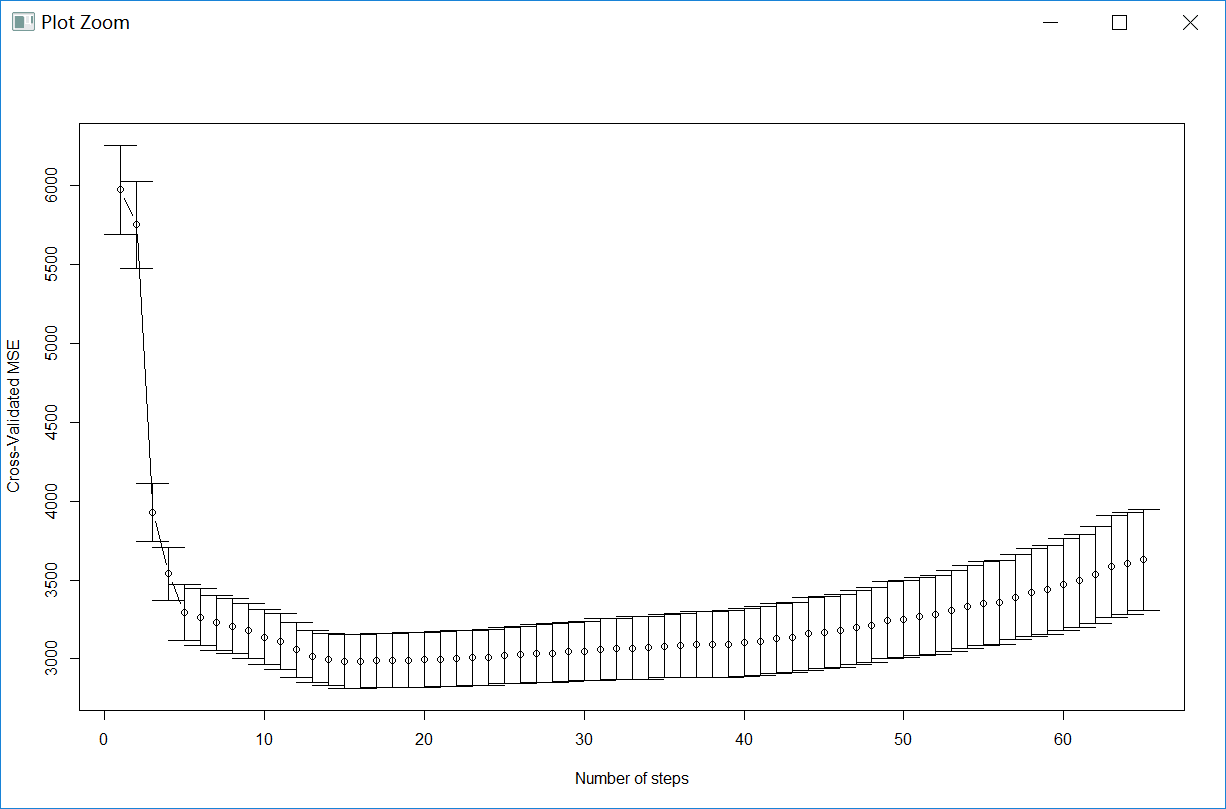
得到交叉验证的均方误差MSE分析结果图如下,

我可以看到由交叉验证得到的最优回归系数（使得均方误差MSE最小）是稀疏的，然后用以下语句得出最优解对应地的step步数为15，

> cvsol1$index[which.min(www.yibaoyule1.com/ cvsol1$cv)]
[1] 15

相应地，第15步对应的的回归系数以及其饱和度|bata|/max|beta|为

得到的回归系数beta的稀疏度为14与真实稀疏度相近, 此处计算其饱和度是为了接下来与用饱和度为 index确定回归系数做对比。

接下来我们用饱和度作为inedx来确定最优, 此处我们已知最优的饱和度大致在0和0.1之间，为便于对比，这里设置饱和度的区间为0：100：0.1

data(diabetes)
attach(diabetes)
cvsol2<-cv.lars(x2,y,type="lar",mode="fraction"，
index=seq(from=0,to=0.1,length=100) )
detach(diabetes)

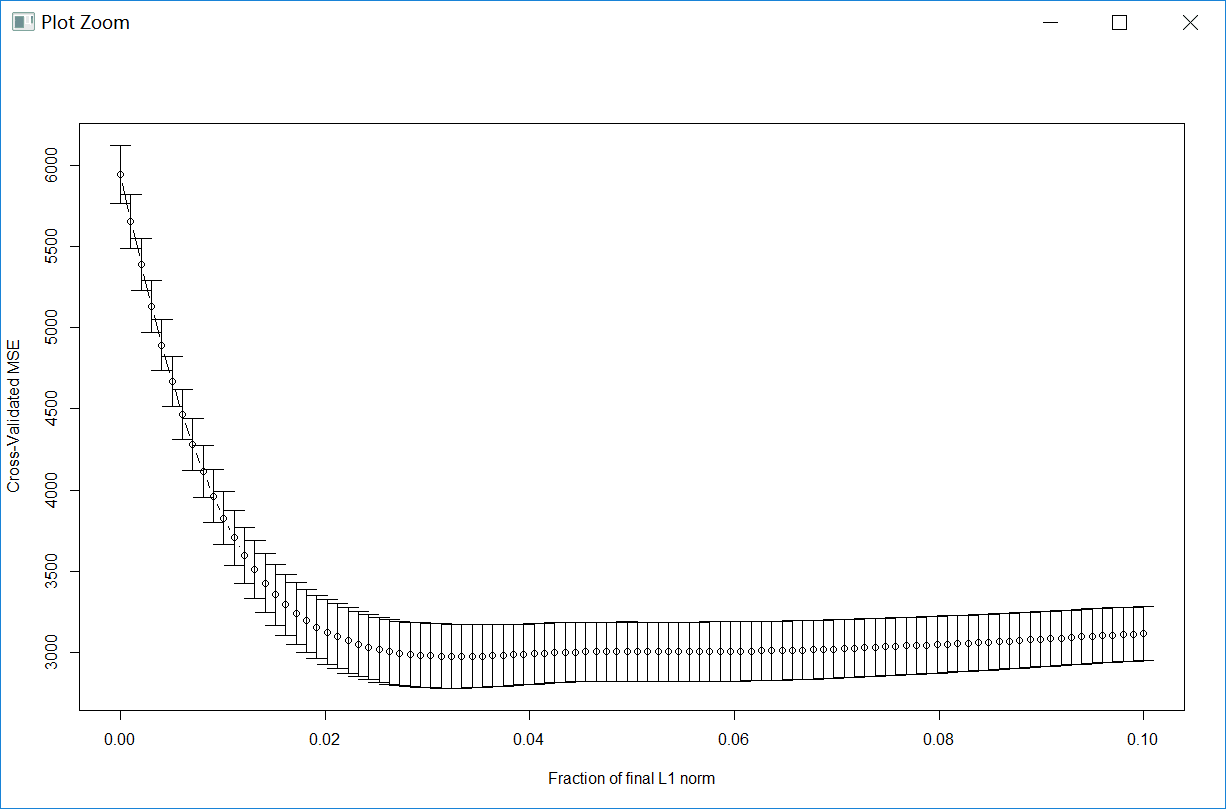
得到的均方误差MSE分析图为

然后同样是提取其中使得均方误差最小的饱和度，得到的结果为0.03232323