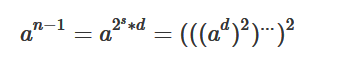大素数测试的Miller-Rabin算法
Miller-Rabin算法本质上是一种概率算法,存在误判的可能性,但是出错的概率非常小。出错的概率到底是多少,存在严格的理论推导。
一、费马小定理
假如p是质数,且gcd(a,p)=1,那么 a(p-1)≡1(mod p)
如果存在a<p,且a(p-1) % p != 1,则p肯定不是素数。
二、有限域上的平方根定理
三、Miller-Rabin算法
对于一个大数n,判断n是不是素数的时候,可以先考虑a(n-1)≡ 1(mod n)
对于n-1,一定可以拆分成2s+d:
可以从x = ad开始,依次平方s次,每次平方的时候模上n,按照之前的平方根定理,如果模上n的结果为1的话,那么x一定是1,或者是n-1,如果不满足则不是素数,x=x2,再次循环。
每次随机选一个在2-n-1的数字作为a,可以重复测试。
由于mod上的是n,n是一个大数,所以快速幂中的乘法,需要用快速加法来实现。不然就算模上之后再相乘也会溢出。
#include<iostream>
#include<ctime>
#include<algorithm>
using namespace std;
typedef long long ll;
const int maxn = +;
ll mul(ll a, ll b, ll m)
//求a*b%m
{
ll ans = ;
a %= m;
while(b)
{
if(b & )ans = (ans + a) % m;
b /= ;
a = (a + a) % m;
}
return ans;
}
ll pow(ll a, ll b, ll m)
//a^b % m
{
ll ans = ;
a %= m;
while(b)
{
if(b & )ans = mul(a, ans, m);
b /= ;
a = mul(a, a, m);
}
ans %= m;
return ans;
}
bool Miller_Rabin(ll n, int repeat)//n是测试的大数,repeat是测试重复次数
{
if(n == || n == )return true;//特判
if(n % == || n == )return false;//偶数和1 //将n-1分解成2^s*d
ll d = n - ;
int s = ;
while(!(d & )) ++s, d >>= ;
srand((unsigned)time(NULL));
for(int i = ; i < repeat; i++)//重复repeat次
{
ll a = rand() % (n - ) + ;//取一个随机数,[2,n-1)
ll x = pow(a, d, n);
ll y = ;
for(int j = ; j < s; j++)
{
y = mul(x, x, n);
if(y == && x != && x != (n - ))return false;
x = y;
}
if(y != )return false;//费马小定理
}
return true;
}
int main()
{
int T;
cin >> T;
ll n;
while(T--)
{
cin >> n;
if(Miller_Rabin(n, ))cout<<"Yes"<<endl;
else cout<<"No"<<endl;
}
}
大素数测试的Miller-Rabin算法的更多相关文章
- 【数论基础】素数判定和Miller Rabin算法
判断正整数p是否是素数 方法一 朴素的判定
- Miller Rabin算法详解
何为Miller Rabin算法 首先看一下度娘的解释(如果你懒得读直接跳过就可以反正也没啥乱用:joy:) Miller-Rabin算法是目前主流的基于概率的素数测试算法,在构建密码安全体系中占有重 ...
- Miller Rabin算法学习笔记
定义: Miller Rabin算法是一个随机化素数测试算法,作用是判断一个数是否是素数,且只要你脸不黑以及常数不要巨大一般来讲都比\(O(\sqrt n)\)的朴素做法更快. 定理: Miller ...
- Miller Rabin 算法简介
0.1 一些闲话 最近一次更新是在2019年11月12日.之前的文章有很多问题:当我把我的代码交到LOJ上,发现只有60多分.我调了一个晚上,尝试用{2, 3, 5, 7, 11, 13, 17, 1 ...
- Miller_Rabbin大素数测试
伪素数: 如果存在和n互素的正整数a满足a^(n-1)≡1(mod n),则n是基于a的伪素数. 是伪素数但不是素数的个数是非常非常少的,所以如果一个数是伪素数,那么他几乎是素数. Miller_Ra ...
- Pollard rho算法+Miller Rabin算法 BZOJ 3668 Rabin-Miller算法
BZOJ 3667: Rabin-Miller算法 Time Limit: 60 Sec Memory Limit: 512 MBSubmit: 1044 Solved: 322[Submit][ ...
- 关于素数:求不超过n的素数,素数的判定(Miller Rabin 测试)
关于素数的基本介绍请参考百度百科here和维基百科here的介绍 首先介绍几条关于素数的基本定理: 定理1:如果n不是素数,则n至少有一个( 1, sqrt(n) ]范围内的的因子 定理2:如果n不是 ...
- (Miller Rabin算法)判断一个数是否为素数
1.约定 x%y为x取模y,即x除以y所得的余数,当x<y时,x%y=x,所有取模的运算对象都为整数. x^y表示x的y次方.乘方运算的优先级高于乘除和取模,加减的优先级最低. 见到x^y/z这 ...
- 米勒罗宾素性测试(Miller–Rabin primality test)
如何判断一个素是素数 效率很高的筛法 打个表 (素数的倍数一定是合数) 就可以解决问题. 筛选法的效率很高,但是遇到大素数就无能为力了. 米勒罗宾素性测试是一个相当著名的判断是否是素数的算法 核心为费 ...
- Miller-Rabin大素数测试模板
根据费马小定理: 对于素数n,a(0<a<n),a^(n-1)=1(mod n) 如果对于一个<n的正整数a,a^(n-1)!=1(mod n),则n必不是素数. 然后就可以随机生成 ...
随机推荐
- Spring Service、Dao进行Junit单元测试
pring对Controller.Service.Dao进行Junit单元测试总结 所有用Junit进行单元测试,都需要下面的配置 @RunWith(SpringJUnit4ClassRunner ...
- Java通过流对MP4视频文件进行加密,H5 video播放流
加密目标文件 代码如下: 不建议进行二次加密,若二次加密必须要二次解密 package com.xgt.util; import java.io.*; public class VideoEncode ...
- Git命令学习笔记
一.本地代码增,删,改,查,提交,找回git checkout . //抛弃工作区所有修改git checkout -- <file> //抛弃工作区& ...
- .netCore2.0 依赖注入
依赖注入(ID)是一种实现对象及其合作者或者依赖想之间松散耦合的技术对于传统的方法来说,获取类的方法通常用new如下 public class DIController : Controller { ...
- Ajax发送GET、POST请求和响应XML数据案例
1.新建工程 新建一个java web工程,新建一个Servlet文件 AServlet.java,用于返回get和post请求. public class AServlet extends Http ...
- django基础一:web、wsgi、mvc、mtv
一.web框架 web框架,即framework,特指为解决一个开放性问题而设计的具有一定约束性的支撑结构,使用框架可以快速开发特定的系统.他山之石,可以攻玉.python的所有web框架,都是对so ...
- IntelliJ IDEA 16创建Web项目
首先要理解一个概念:在IntelliJ IDEA中“new Project”相当于eclipse中的工作空间(Workspace),而“new Module”相当于eclipse中的工程(Projec ...
- ccf-201709-2 公共钥匙盒
问题描述 有一个学校的老师共用N个教室,按照规定,所有的钥匙都必须放在公共钥匙盒里,老师不能带钥匙回家.每次老师上课前,都从公共钥匙盒里找到自己上课的教室的钥匙去开门,上完课后,再将钥匙放回到钥匙盒中 ...
- 用css3+js写了一个钟表
有一天看到css3旋转这个属性,突发奇想的写了一个钟表(没做浏览器兼容),来一起看看是怎么写的吧! 先给个成品图,最终结果是个样子的(动态的). 首先,思考了一下页面的布局,大致需要4层div,最底层 ...
- ogr2ogr使用
简介 org2ogr是OGR模块中提供的一个重要工具,用于对数据源进行格式转换 使用方式 命令行参数 [xingxing.dxx@30_28_6_20 J50F001020]$ ogr2ogr --l ...