Java实现最优二叉查找树

1 问题描述

在了解最优二叉查找树之前，我们必须先了解何为二叉查找树？

引用自百度百科一段讲解：

二叉排序树（Binary Sort Tree）又称二叉查找树（Binary Search Tree），亦称二叉搜索树。

二叉排序树或者是一棵空树，或者是具有下列性质的二叉树：

（1）若左子树不空，则左子树上所有结点的值均小于或等于它的根结点的值；

（2）若右子树不空，则右子树上所有结点的值均大于或等于它的根结点的值；

（3）左、右子树也分别为二叉排序树；

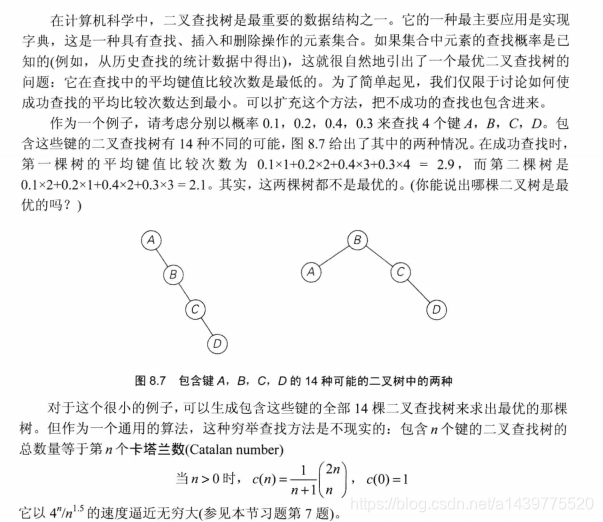
在二叉查找树的基础上，引出了一个最优二叉查找树的问题：它在查找树中所有节点的平均键值比较次数是最低的。（PS：如若对于最优二叉查找树的定义理解还是有点模糊，可以参考本文最后给出的参考资料中的链接）

2 解决方案

本文具体编码思想参考自《算法设计与分析基础》第三版，具体如下（PS：对于文中的具体思想，楼主自己是前后看了三四遍才整明白其具体思想，竟无语吟噎…，如若对于下面贴出的书中介绍无法理解，可以参考文末给出的参考资料的链接中，一位网友的博客讲解哦）：

package com.liuzhen.chapter8;

public class OptimalBST {
    /*
     * 参数P：表示1~n个节点的查找概率。其中P[0] = 0，无意义
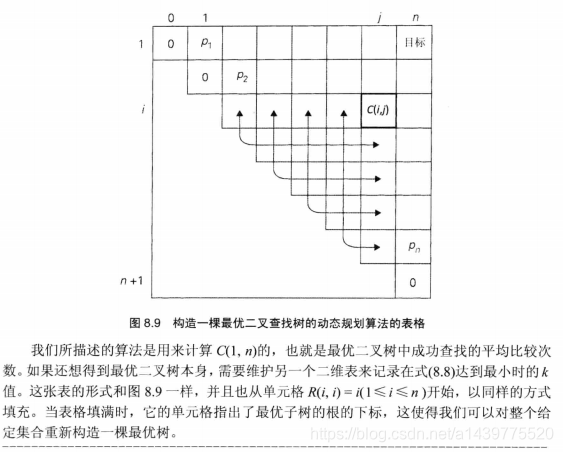
     * 函数功能：返回在最优BST中查找的平均比较次数主表C[][]，以及最优BST中子树的根表R
     */
    public void getBestTree(double[] P) {
        int lenP = P.length;
        double[][] C = new double[lenP+1][lenP];   //保存最有BST的成功查找的平均比较次数
        int[][] R = new int[lenP+1][lenP];   //保存最优BST中子树的根表R
        for(int i = 1;i < lenP;i++) {
            C[i][i] = P[i];
            R[i][i] = i;
        }

        for(int d = 1;d < lenP-1;d++) {
            for(int i = 1;i < lenP-d;i++) {
                int j = i + d;
                double minval = Double.MAX_VALUE;     //以double类型的最大值，表示minval趋向无穷大
                int kmin = 0;
                for(int k = i;k <= j;k++) {
                    if(C[i][k-1] + C[k+1][j] < minval) {
                        minval = C[i][k-1] + C[k+1][j];
                        kmin = k;
                    }
                }
                R[i][j] = kmin;
                double sum = P[i];
                for(int s = i+1;s <= j;s++)
                    sum += P[s];
                C[i][j] = minval + sum;
            }
        }

        System.out.println("在最优BST中查找的平均比较次数依次为：");
        for(int i = 1;i < C.length;i++) {
            for(int j = 0;j < C[0].length;j++)
                System.out.printf("%.1f\t",C[i][j]);
            System.out.println();
        }

        System.out.println("在最优BST中子树的根表R为：");
        for(int i = 1;i < R.length;i++) {
            for(int j = 0;j < R[0].length;j++)
                System.out.print(R[i][j]+"\t");
            System.out.println();
        }
    }

    public static void main(String[] args) {
        OptimalBST test = new OptimalBST();
        double[] P = {0,0.1,0.2,0.4,0.3};
        test.getBestTree(P);
    }

}

运行结果：

在最优BST中查找的平均比较次数依次为：
0.0    0.1    0.4    1.1    1.7
0.0    0.0    0.2    0.8    1.4
0.0    0.0    0.0    0.4    1.0
0.0    0.0    0.0    0.0    0.3
0.0    0.0    0.0    0.0    0.0
在最优BST中子树的根表R为：
   1    2    3    3
   0    2    3    3
   0    0    3    3
   0    0    0    4
   0    0    0    0