MATLAB实现一个EKF-2D-SLAM（已开源）

1. SLAM问题定义

同时定位与建图（SLAM）的本质是一个估计问题，它要求移动机器人利用传感器信息实时地对外界环境结构进行估计，并且估算出自己在这个环境中的位置，Smith 和Cheeseman在上个世纪首次将EKF估计方法应用到SLAM。

以滤波为主的SLAM模型主要包括三个方程：

1）运动方程：它会增加机器人定位的不确定性

2）根据观测对路标初始化的方程：它根据观测信息，对新的状态量初始化。

3）路标状态对观测的投影方程：根据观测信息，对状态更新，纠正，减小不确定度。

2. EKF-SLAM维护的数据地图

系统状态x是一个很大的向量，它包括机器人的状态和路标点的状态，

\[ \mathbf{x}=\left[\begin{array}{c}
{\mathcal{R}} \\
{\mathcal{M}}
\end{array}\right]=\left[\begin{array}{c}
{\mathcal{R}} \\
{\mathcal{L}_{1}} \\
{\vdots} \\
{\mathcal{L}_{n}}
\end{array}\right]
\]

其中\({\mathcal{R}}\)是机器人状态，\({\mathcal{M}} = \left({\mathcal{L}_{1}}， \dots，{\mathcal{L}_{n}}\right)\)是n个当前已经观测过的路标点状态集合。

在EKF中，x被认为服从高斯分布，所以，EKF-SLAM的地图被建模为x的均值\(\overline{x}\)与协方差\(\mathbf{P}\),

\[ \overline{\mathbf{x}}=\left[\frac{\overline{\mathcal{R}}}{\mathcal{M}}\right]=\left[\begin{array}{c}
{\overline{\mathcal{R}}} \\
{\overline{\mathcal{L}}_{1}} \\
{\vdots} \\
{\overline{\mathcal{L}}_{n}}
\end{array}\right] \quad \mathbf{P}=\left[\begin{array}{cc}
{\mathbf{P}_{\mathcal{R} \mathcal{R}}} & {\mathbf{P}_{\mathcal{R} \mathcal{M}}} \\
{\mathbf{P}_{\mathcal{M R}}} & {\mathbf{P}_{\mathcal{M M}}}
\end{array}\right]=\left[\begin{array}{cccc}
{\mathbf{P}_{\mathcal{R R}}} & {\mathbf{P}_{\mathcal{R} \mathcal{L}_{1}}} & {\cdots} & {\mathbf{P}_{\mathcal{R} \mathcal{L}_{n}}} \\
{\mathbf{P}_{\mathcal{L}_{1} \mathcal{R}}} & {\mathbf{P}_{\mathcal{L}_{1} \mathcal{L}_{1}}} & {\cdots} & {\mathbf{P}_{\mathcal{L}_{n}} \mathcal{L}_{n}} \\
{\vdots} & {\vdots} & {\ddots} & {\vdots} \\
{\mathbf{P}_{\mathcal{L}_{n} \mathcal{R}}} & {\mathbf{P}_{\mathcal{L}_{n} \mathcal{L}_{1}}} & {\cdots} & {\mathbf{P}_{\mathcal{L}_{n} \mathcal{L}_{n}}}
\end{array}\right]
\]

因此EKF-SLAM的目标就是根据运动模型和观测模型及时更新地图量\(\left\{\overline{\mathbf{x}},\mathbf{P}\right\}\)

3. EKF-SLAM算法实施

3.1 地图初始化

显而易见，在机器人开始之前是没有任何路标点的信息的，因此此时地图中只有机器人自己的状态信息，因此\({n} = 0,{x} = {\mathcal{R}}\)。SLAM中经常把机器人初始位姿认为是地图的原点，其初始协方差可以按实际情况设定，比如：

\[ \overline{\mathbf{x}}=\left[\begin{array}{l}
{x} \\
{y} \\
{\theta}
\end{array}\right]=\left[\begin{array}{l}
{0} \\
{0} \\
{0}
\end{array}\right] \quad \mathbf{P}=\left[\begin{array}{lll}
{0} & {0} & {0} \\
{0} & {0} & {0} \\
{0} & {0} & {0}
\end{array}\right]
\]

3.2 运动模型

在EKF中如果x是状态量，u是控制输入，n是噪声变量，那么我们可以得到一般的状态更新函数：

\[\mathbf{x} \leftarrow f(\mathbf{x}, \mathbf{u}, \mathbf{n})
\]

EKF的预测步骤为：

\[\begin{array}{l}
{\overline{\mathbf{x}} \leftarrow f(\overline{\mathbf{x}}, \mathbf{u}, 0)} \\
{\mathbf{P} \leftarrow \mathbf{F}_{\mathbf{x}} \mathbf{P} \mathbf{F}_{\mathbf{x}}^{\top}+\mathbf{F}_{\mathbf{n}} \mathbf{N} \mathbf{F}_{\mathbf{n}}^{\top}}
\end{array}
\]

其中雅克比矩阵\(\mathbf{F}_{\mathbf{x}}=\frac{\partial f(\overline{\mathbf{x}}, \mathbf{u})}{\partial \mathbf{x}}\)，\(\mathbf{F}_{\mathbf{n}}=\frac{\partial f(\overline{\mathbf{x}}, \mathbf{u})}{\partial \mathbf{n}}\)，\({\mathbf{N}}\)是随机变量n的协方差。

但是在EKF-SLAM中，只有一部分状态\({\mathcal{R}}\)是随运动而改变的，其余所有路标状态不改变，所以SLAM的运动方程为：

\[\begin{array}{l}
{\mathcal{R} \leftarrow f_{\mathcal{R}}(\mathcal{R}, \mathbf{u}, \mathbf{n})} \\
{\mathcal{M} \leftarrow \mathcal{M}}
\end{array}
\]

因此我们可以得到稀疏的雅克比矩阵：

\[ \mathbf{F}_{\mathbf{x}}=\left[\begin{array}{cc}
{\frac{\partial f_{\mathcal{R}}}{\partial \mathcal{R}}} & {0} \\
{0} & {\mathbf{I}}
\end{array}\right] \quad \mathbf{F}_{\mathbf{n}}=\left[\begin{array}{c}
{\frac{\partial f_{\mathcal{R}}}{\partial \mathbf{n}}} \\
{0}
\end{array}\right]
\]

最终我们得到了用于运动模型的EKF稀疏预测公式

\[\overline{\mathcal{R}} \leftarrow f_{\mathcal{R}}(\overline{\mathcal{R}}, \mathbf{u}, 0)
\]

\[ \mathbf{P}_{\mathcal{R} \mathcal{R}} \leftarrow \frac{\partial f_{\mathcal{R}}}{\partial \mathcal{R}} \mathbf{P}_{\mathcal{R} \mathcal{R}} \frac{\partial f_{\mathcal{R}}^{T}}{\partial \mathcal{R}}+\frac{\partial f_{\mathcal{R}}}{\partial \mathbf{n}} \mathbf{N} \frac{\partial f_{\mathcal{R}}^{T}}{\partial \mathbf{n}}
\]

\[\mathbf{P}_{\mathcal{R} \mathcal{M}} \leftarrow \frac{\partial f_{\mathcal{R}}}{\partial \mathcal{R}} \mathbf{P}_{\mathcal{R} \mathcal{M}}
\]

\[ \mathbf{P}_{\mathcal{M} \mathcal{R}} \leftarrow \mathbf{P}_{\mathcal{R} \mathcal{M}}^{\top}
\]

3.3 已经加入地图的状态量观测更新

在EKF中，我们有以下一般的观测方程

\[ \mathbf{y}=h(\mathbf{x})+\mathbf{v}
\]

其中\(\mathbf{y}\)是测量噪声，\(\mathbf{x}\)是全状态，\(h()\)是观测函数，\(v\)是测量噪声。

典型的EKF观测更新为：

\[ \overline{\mathbf{z}}=\mathbf{y}-h(\overline{\mathbf{x}})
\]

\[\mathbf{Z}=\mathbf{H}_{\mathbf{x}} \mathbf{P} \mathbf{H}_{\mathbf{x}}^{\top}+\mathbf{R}
\]

\[ \mathbf{K}=\mathbf{P} \mathbf{H}_{\mathbf{x}}^{\top} \mathbf{Z}^{-1}
\]

\[\overline{\mathbf{x}} \leftarrow \overline{\mathbf{x}}+\mathbf{K} \overline{\mathbf{z}}
\]

\[ \mathbf{P} \leftarrow \mathbf{P}-\mathbf{K} \mathbf{Z} \mathbf{K}^{\top}
\]

雅克比矩阵\(\mathbf{H}_{\mathbf{x}}=\frac{\partial h(\overline{\mathbf{x}})}{\partial \mathbf{x}}\)，\(\mathbf{R}\)是测量噪声的协方差矩阵。

在SLAM中，观测指的是机器人上的传感器观测到某些路标点，并对路标点进行参数化的输出。每次可能对路标点有多个观测值，这里每使用一个观测值，就进行一次状态更新。

观测的结果依赖于机器人的状态\(\mathcal{R}\),传感器的状态\(\mathcal{S}\)和路标点的状态\(\mathcal{L}_{i}\)，并且这里假设，传感器的状态与机器人的状态差了一个固定的坐标变化，其实也就是外参固定。当观测到路标点\(i\)时，可以得到如下关系：

\[ \mathbf{y}_{i}=h_{i}\left(\mathcal{R}, \mathcal{S}, \mathcal{L}_{i}\right)+\mathbf{v}
\]

这就是观测方程，它不依赖于除了\(\mathcal{L}_{i}\)外的任何路标点状态。因此EKF-SLAM的雅克比\(\mathbf{H}_{\mathbf{x}}\)也是稀疏的：

\[ \mathbf{H}_{\mathbf{x}}=\left[\begin{array}{lllllllll}
{\mathbf{H}_{\mathcal{R}}} & {0} & {\cdots} & {0} & {\mathbf{H}_{\mathcal{L}_{i}}} & {0} & {\cdots} & {0}
\end{array}\right]
\]

其中\(\mathbf{H}_{\mathcal{R}}=\frac{\partial h_{i}\left(\overline{\mathcal{R}}, \mathcal{S}, \overline{\mathcal{L}}_{i}\right)}{\partial \mathcal{R}}\)，\(\mathbf{H}_{\mathcal{L}_{i}}=\frac{\partial h_{i}\left(\overline{\mathcal{R}}, \mathcal{S}, \overline{\mathcal{L}}_{i}\right)}{\partial \mathcal{L}_{i}}\)。由于这里的稀疏性，EKF-SLAM的观测更新变成：

\[\overline{\mathbf{z}}=\mathbf{y}_{i}-h_{i}\left(\overline{\mathcal{R}}, \mathcal{S}, \overline{\mathcal{L}}_{i}\right)
\]

\[ \mathbf{Z}=\left[\begin{matrix}\mathbf{H}_{\mathcal{R}} &\mathbf{H}_{\mathcal{L}_{i}}\end{matrix}\right]\left[\begin{array}{cc}
{\mathbf{P}_{\mathcal{R} \mathcal{R}}} & {\mathbf{P}_{\mathcal{R} \mathcal{L}_{i}}} \\
{\mathbf{P}_{\mathcal{L}_{i} \mathcal{R}}} & {\mathbf{P}_{\mathcal{L}_{i} \mathcal{L}_{i}}}
\end{array}\right]\left[\begin{array}{c}
{\mathbf{H}_{\mathcal{R}}^{\top}} \\
{\mathbf{H}_{\mathcal{L}_{i}}^{\top}}
\end{array}\right]+\mathbf{R}
\]

\[\mathbf{K}=\left[\begin{array}{ll}
{\mathbf{P}_{\mathcal{R} \mathcal{R}}} & {\mathbf{P}_{\mathcal{R} \mathcal{L}_{i}}} \\
{\mathbf{P}_{\mathcal{M} \mathcal{R}}} & {\mathbf{P}_{\mathcal{M} \mathcal{L}_{i}}}
\end{array}\right]\left[\begin{array}{l}
{\mathbf{H}_{\mathcal{R}}^{\top}} \\
{\mathbf{H}_{\mathcal{L}_{i}}^{\top}}
\end{array}\right] \mathbf{Z}^{-1}
\]

\[ \overline{\mathbf{x}} \leftarrow \overline{\mathbf{x}}+\mathbf{K} \overline{\mathbf{z}}
\]

\[\mathbf{P} \leftarrow \mathbf{P}-\mathbf{K} \mathbf{Z} \mathbf{K}^{\top}
\]

3.4 观测方程可逆时的状态增广

这里的状态增广指的是新发现的路标点的初始化。当机器人发现了曾经未观测到的路标点时，会利用观测方程将新的路标状态加入地图，这一步操作会增大总状态向量的大小。可以看到EKF-SLAM中的滤波器大小动态变化的。

当传感器信息可以提供新发现路标点的所有自由度，也就是观测方程是双射时，只需要根据观测方程\(h()\)的逆运算，即可以得到机器人状态\(\mathcal{R}\)，传感器状态\(\mathcal{S}\)，观测量\(\mathbf{y}_{n+1}\)，观测噪声\(v\)，它们与新路标点状态的关系：

\[ \mathcal{L}_{n+1}=g\left(\mathcal{R}, \mathcal{S}, \mathbf{y}_{n+1},v\right)
\]

上式是单个路标点的逆观测模型。

路标点的均值和雅克比：

\[ \overline{\mathcal{L}}_{n+1}=g\left(\overline{\mathcal{R}}, \mathcal{S}, \mathbf{y}_{n+1},0\right)
\]

\[\mathbf{G}_{\mathcal{R}}=\frac{\partial g\left(\overline{\mathcal{R}}, \mathcal{S}, \mathbf{y}_{n+1},0\right)}{\partial \mathcal{R}}
\]

\[ \mathbf{G}_{\mathbf v}=\frac{\partial g\left(\overline{\mathcal{R}}, \mathcal{S}, \mathbf{y}_{n+1},0\right)}{\partial \mathbf{v}}
\]

显然，新加路标点状态的协方差\(\mathbf{P}_{\mathcal{L} \mathcal{L}}\)，以及该状态与地图其它状态的互协方差为：

\[ \mathbf{P}_{\mathcal{L} \mathcal{L}}=\mathbf{G}_{\mathcal{R}} \mathbf{P}_{\mathcal{R} \mathcal{R}} \mathbf{G}_{\mathcal{R}}^{\top}+\mathbf{G}_{\mathbf v} \mathbf{R} \mathbf{G}_{\mathbf v}^{\top}
\]

\[\mathbf{P}_{\mathcal{L} \mathbf{x}}=\mathbf{G}_{\mathcal{R}} \mathbf{P}_{\mathcal{R} \mathbf{x}}=\mathbf{G}_{\mathcal{R}}\left[\begin{matrix}\mathbf{P}_{\mathcal{R} \mathcal{R}} &\mathbf{P}_{\mathcal{R} \mathcal{M}}\end{matrix}\right]
\]

然后将这些结果加入到地图中，可以得到总状态的均值与协方差矩阵：

\[ \overline{\mathbf{x}} \leftarrow
\left[\begin{array}{c}
{\overline{\mathbf{x}}} \\
{\overline{\mathcal{L}}_{n+1}}
\end{array}\right]
\]

\[ \mathbf{P} \leftarrow\left[\begin{array}{cc}
{\mathbf{P}} & {\mathbf{P}_{\mathcal{L} \mathbf{x}}^{\top}} \\
{\mathbf{P}_{\mathcal{L}\mathbf{x}}} & {\mathbf{P}_{\mathcal{L}\mathcal{L}}}
\end{array}\right]
\]

4. 仿真实验

4.1 模型设置

4.1.1 传感器模型

传感器是一个360度的雷达，可以探测发现周围一定范围内的路标点及其类型，其探测半径为r，其观测值为(\(\xi\)，s)。\(\xi\)为在当前雷达坐标系中路标点与x轴的的夹角，s为路标点与当前雷达坐标系原点的距离。

4.1.2 运动模型

将当前时刻雷达局部坐标系中的（\({u}_{1}\),0）点作为下一时刻雷达的位置，所以运动方程可以设为：

\[ \left[\begin{array}{cc}
{x_{n}} \\
{y_{n}}
\end{array}
\right] =
\left[\begin{array}{cc}
cos\theta_{n-1} & -sin\theta_{n-1} \\
sin\theta_{n-1} & cos\theta_{n-1}
\end{array}\right]
\left[\begin{array}{cc}
{u}_{1} \\
0
\end{array}\right] +
\left[\begin{array}{cc}
{x_{n-1}} \\
{y_{n-1}}
\end{array}
\right] +
\left[\begin{array}{cc}
{n}_{1} \\
0
\end{array}
\right]
\]

其方位每次增加固定的\(u_2\):

\[ {\theta_{n+1}} = {\theta_n} + {u}_{2} + {n}_{2}
\]

其中\(n_1,n_2\)为系统噪声。

4.1.3 观测模型

设路标点\(i\)的状态为\(x_{L_i}=\)(\(m_1\)，\({m}_{2}\))，则其在当前雷达坐标系的坐标为：

\[ \left[\begin{array}{cc}
{{{ladar}_{1}}} \\
{{{ladar}_{2}}}
\end{array}
\right] =
{\left[\begin{array}{cc}
cos\theta_n & -sin\theta_n \\
sin\theta_n & cos\theta_n
\end{array}\right]}^{-1}
\left[\begin{array}{cc}
{{{m}_{1}}} \\
{{{m}_{2}}}
\end{array}
\right] -
\left[\begin{array}{cc}
{x_n} \\
{y_n}
\end{array}
\right]
\]

则观测量为：

\[ \xi = atan2\left({{{ladar}_{2}}},{{{ladar}_{1}}}\right) + {v}_{1}
\]

\[ s = \sqrt{{\left({{{ladar}_{1}}}\right)}^{2} + {\left({{{ladar}_{2}}}\right)}^{2}} + {v}_{2}
\]

其中\(v_1,v_2\)为测量噪声。

4.2 实验结果

使用MATLAB编写程序进行仿真。

代码地址:https://github.com/liuzhenboo/EKF-2D-SLAM

4.2.1 第一次状态增广

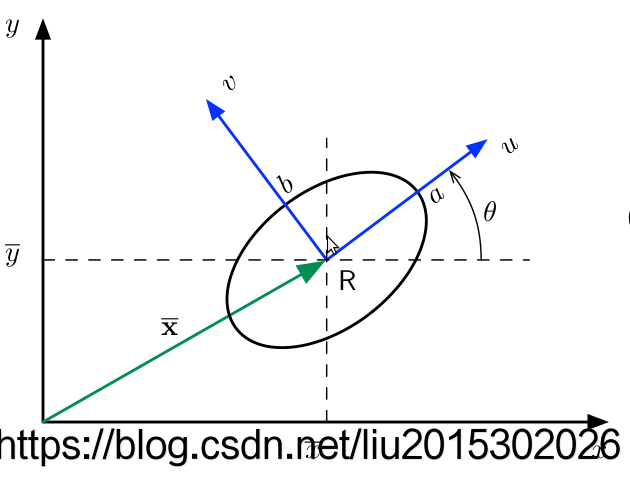
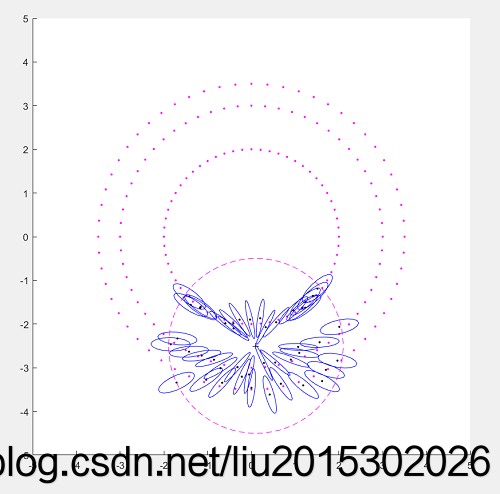
其中左图黑色的点表示滤波器新加入的路标点状态均值，绿色椭圆表征路标状态的协方差，其椭圆方程为：

\[ (\mathbf{x}-\overline{\mathbf{x}})^{\top} \mathbf{P}^{-1}(\mathbf{x}-\overline{\mathbf{x}})=\text { const }
\]

其中x为路标状态, P为路标的协方差。

程序中是对P进行SVD分解，得到椭圆的方向R以及半轴到的长度，进行绘图。

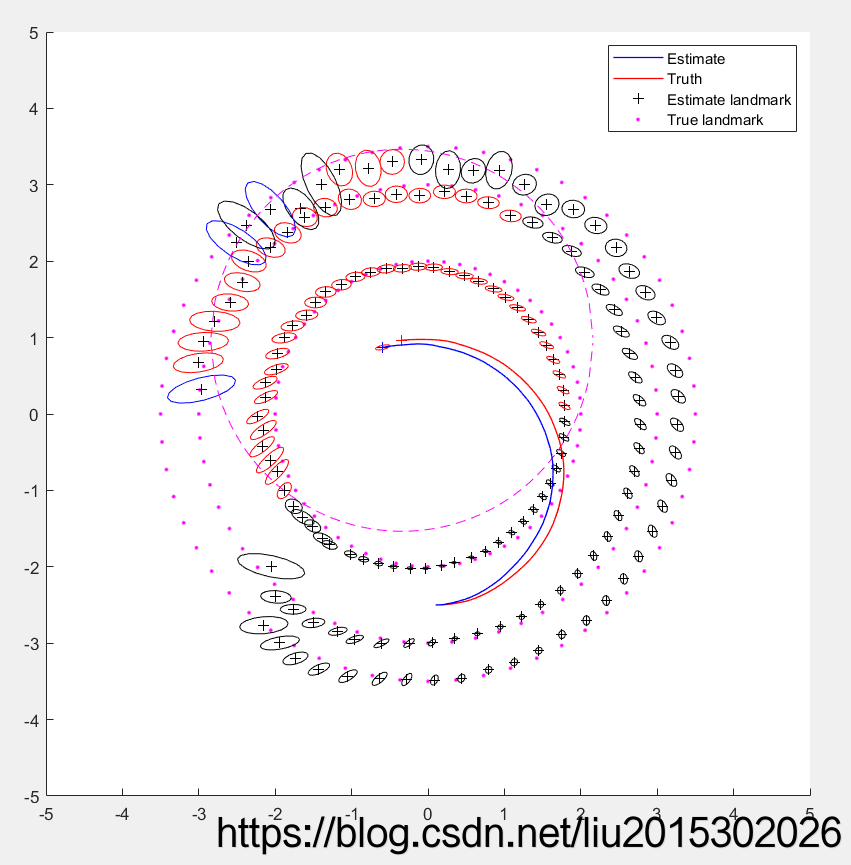
4.2.2 状态增广，观测更新

如上图，黑色椭圆对应的路标点表示雷达曾经观测过它，但是当前时刻没有观测到；红色椭圆对应的路标点表示雷达曾经观测过它，并且当前时刻也观测到了；蓝色代表当前刚刚初始化的新路标点。

注意：由于数值计算的原因，图中几何元素的位置关系可能和实际有些许差别；比如有的路标点明明不在雷达范围内，却开始初始化（绿色），这是因为计算过程中matlab四舍五入导致的结果。

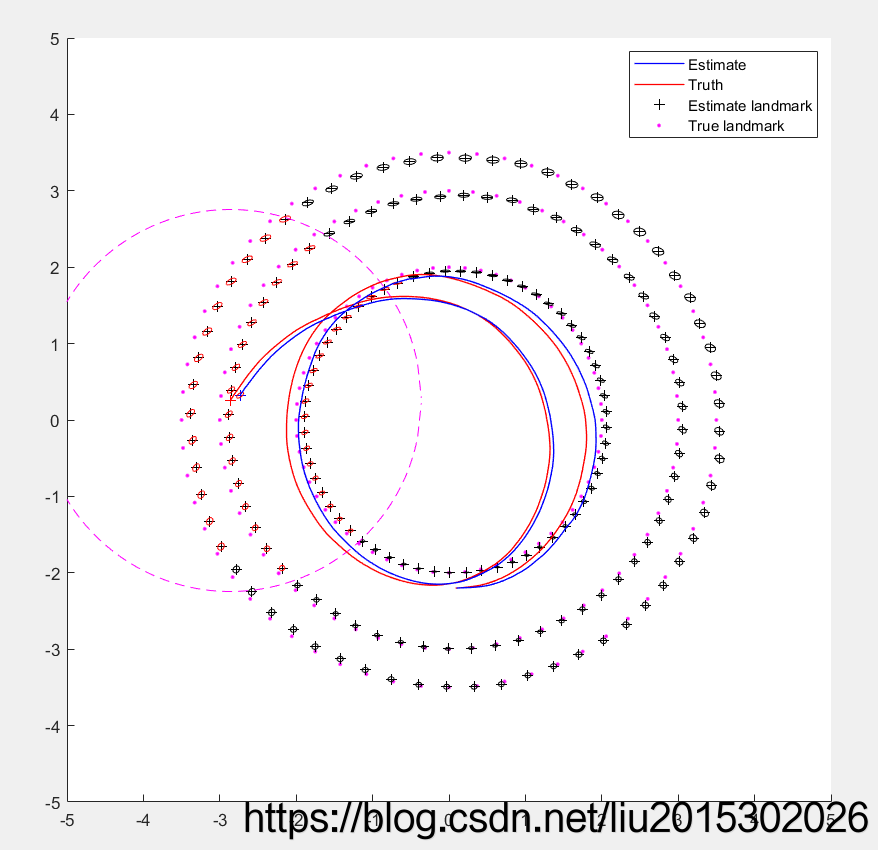
4.2.3 状态不再增广，只有观测更新

如上图，不再存在蓝色的协方差椭圆，代表状态增广停止，滤波器的大小不再改变。