并查集 & 最小生成树

并查集 Disjoint Sets

什么是并查集？

并查集，在一些有N个元素的集合应用问题中，我们通常是在开始时让每个元素构成一个单元素的集合，然后按一定顺序将属于同一组的元素所在的集合合并，其间要反复查找一个元素在哪个集合中。这一类问题近几年来反复出现在信息学的国际国内赛题中，其特点是看似并不复杂，但数据量极大，若用正常的数据结构来描述的话，往往在空间上过大，计算机无法承受；即使在空间上勉强通过，运行的时间复杂度也极高，根本就不可能在比赛规定的运行时间（1～3秒）内计算出试题需要的结果，只能用并查集来描述。

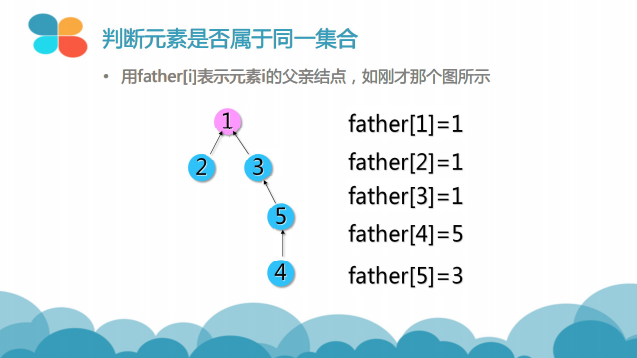
并查集（Disjoint Sets）是一种树型的数据结构，用于处理一些不相交集合的合并及查询问题。常常在使用中以森林来表示。(引自百度百科《并查集》)

简单来说，并查集的主要操作有：

1- 合并两个不相交的集合

2- 查询两个元素是否属于同一个集合

老样子，先上引例——

NKOJ 1205 亲戚

或许你并不知道，你的某个朋友是你的亲戚。他可能是你的曾祖父的外公的女婿的外甥女的表姐的孙子。如果能得到完整的家谱，判断两个人是否亲戚应该是可行的，但如果两个人的最近公共祖先与他们相隔好几代，使得家谱十分庞大，那么检验亲戚关系实非人力所能及。在这种情况下，最好的帮手就是计算机。

　　为了将问题简化，你将得到一些亲戚关系的信息，如同Marry和Tom是亲戚，Tom和Ben是亲戚，等等。从这些信息中，你可以推出Marry和Ben 是亲戚。请写一个程序，对于我们的关于亲戚关系的提问，以最快的速度给出答案。

输入格式：

输入由两部分组成。

第一部分以N，M开始。N为问题涉及的人的个数(1 ≤ N ≤ 20000)。这些人的

编号为1,2,3,…,N。下面有M行(1 ≤ M ≤ 100000)，每行有两个数ai, bi，表示已知ai和bi是亲戚。

第二部分以Q开始。以下Q行有Q个询问(1 ≤ Q ≤ 1 000 000)，每行为ci,di，表示询问ci和di是否为亲戚。

输出格式：

对于每个询问ci, di，若ci和di为亲戚，则输出yes，否则输出no。

样例输入：

10 7

2 4

5 7

1 3

8 9

1 2

5 6

2 3

3

3 4

7 10

8 9

样例输出：

yes

no

yes

传送门：http://oi.nks.edu.cn/zh/Problem/Details?id=1205

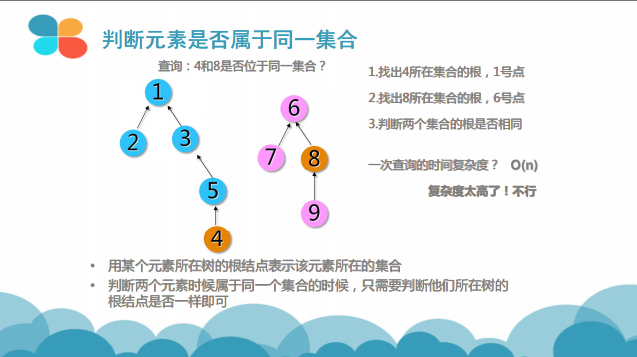
从题目中我们可以得到一些提示，它就是要让我们构建一个关系集合出来，再快速查找两个元素是否位于同一集合，这显然就与并查集的效用十分吻合。

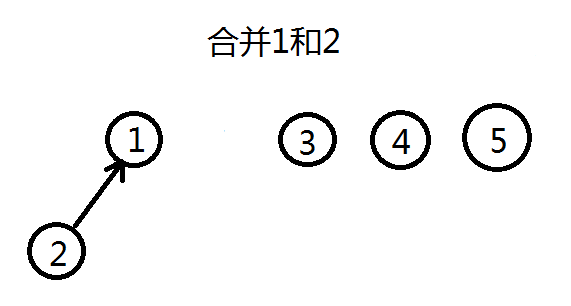
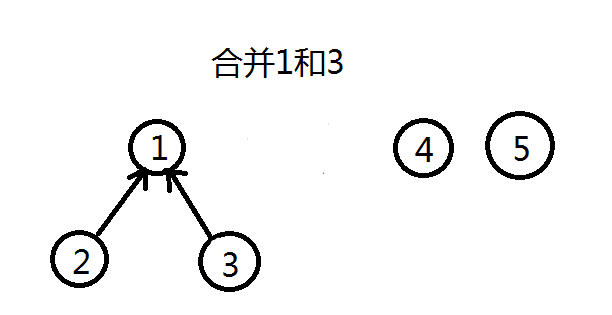
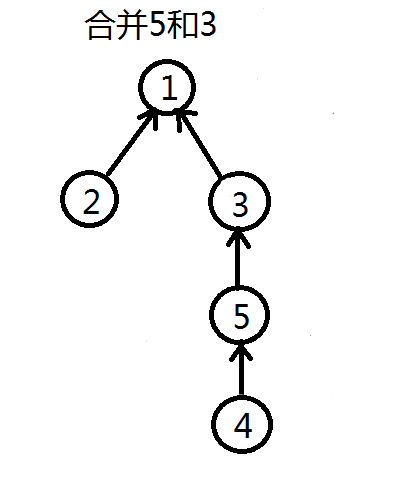
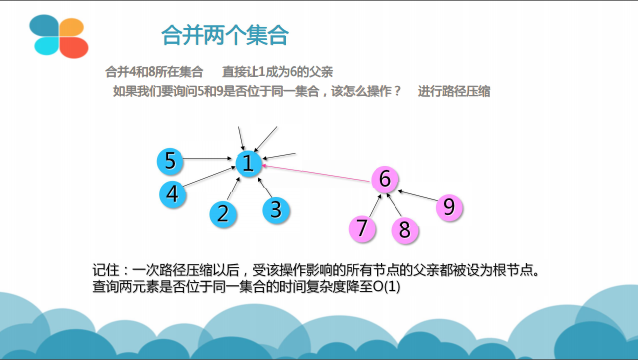
合并的过程是怎样的(图示）？

并查集的工作原理

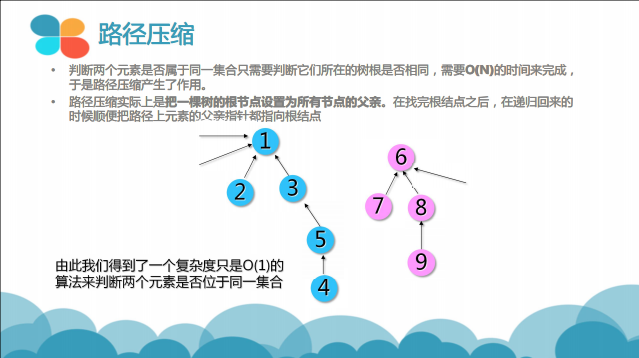
基于此算法如此高的时间复杂度，我们采用某种特殊的手段来优化它，这也便是并查集的核心内容——路径压缩

下面给出并查集的核心函数：

查询同时路径压缩

int GetFather(int v) {	//查询元素v所在集合的根节点
	if (Father[v] == v)return v;	//v本身为根
	else {
		Father[v] = GetFather(Father[v]);	//只对v到根这条路径上的节点进行路径压缩
		return Father[v];
	}
}

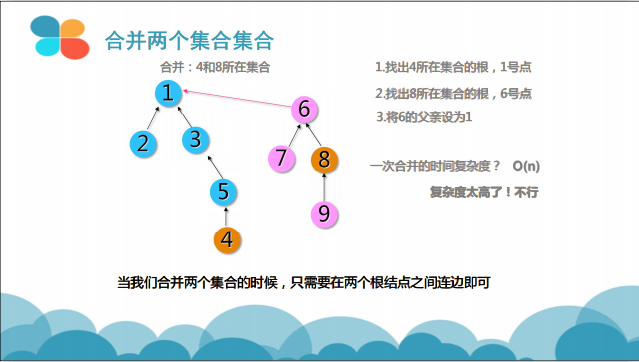
合并两个集合

void Merge(int x, int y) {	//合并元素x和元素y所在集合
	int fx, fy;
	fx = GetFather(x);	//先找出x和y所在集合的根
	fy = GetFather(y);	//两根不相同，说明x和y位于不同集合
	if (fx != fy)Father[fx] = fy;	//将fy设为fx的父亲，合并两个集合
}

我们回到引例，我们现在可以很轻松地解决此题（伪代码）——

for (i = 1; i <= n; ++ i)Father[i] = i;	//初始化
for (i = 1; i <= m; ++ i) {	//读入关系
	cin >> x >> y;
	Merge(x, y);
}
for (i = 1; i <= q; ++ i) {	//回答询问
	cin >> x >> y;
	if (GetFather(x) == GetFather(y))
		cout << "Yes";
	else cout << "No";
}  (O(m))

#######提供几道并查集的简单练习：

NKOJ 3197 岛屿

 NKOJ 1046 关押罪犯

并查集的启发式合并（有缘再补）

最小生成树 Minnimum Spanning Tree(MST)

什么是最小生成树？

一个有 n 个结点的连通图的生成树是原图的极小连通子图，且包含原图中的所有 n 个结点，并且有保持图连通的最少的边。最小生成树可以用kruskal（克鲁斯卡尔）算法或prim（普里姆）算法求出。(引自百度百科《最小生成树》）

简言之，最小生成树就是在一个连通图中生成一棵树，刚好连通所有节点，所含边数（或边权总和最小）。

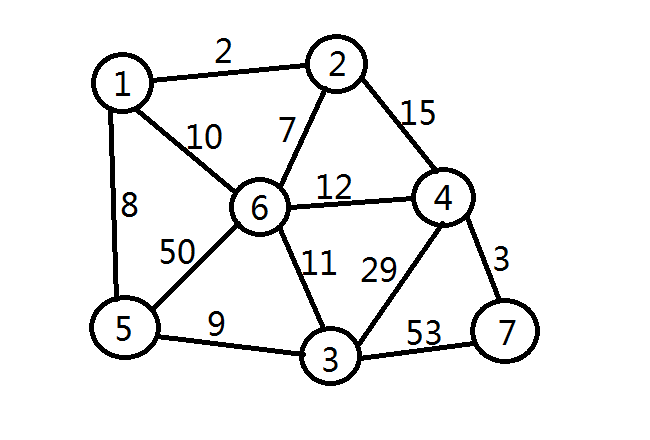
举个栗子，感受一下——

引例：村长的难题

何老板是某乡村的村长，何老板打算给该村的所有人家都连上网。

该村有n(1<=n<=1000)户人家，编号1到n。由于地形等原因，只有

m(1<=m<=50000)对人家之间可以相互牵线。在不同人家间牵线的长度不一定相同。比如在Ai与Bi之间牵线需要Ci米长的网线。

整个村的网络入口在1号人家，何老板的问题是：是否能使得所有人家都连上网？使所有人家都连上网，最少需要多少米网线？

关注这个例子，我们的解法是要用网线连接n户人家，找出一种方案，使得总的长度最少。

我们目测可到样图的最小生成树

可是我们怎么用算法做到呢？

接下来我会介绍三种算法：

1- Kruskal(克鲁斯卡尔算法)

2- Prim(普里姆算法)

3- Boruvka算法

这三种算法都是基于贪心思想的应用，但其中Kruskal可处理同权边的情况，而Boruvka不可以。

Kruskal

Kruskal算法的基本思想：

每次选不属于同一生成树的且权值最小的边的顶点，将边加入生成树，并将所在的2个生成树合并，直到只剩一个生成树。

排序使用Quicksort

检查是否在同一生成树用并查集

总时间复杂度O(mlogm)，其中m表示边的数量

以下是用Kruskal解决引例的代码：

#define maxm 10003
#define maxn 103
struct node {
	int a, b, len;	//a，b表示边的两个顶点，len表示长度
}Edge[maxm];  //边的信息
int n, m;	//n为顶点数，m为边数
int Father[maxn];	//Father[]存i的父亲节点
bool cmp(node a, node b) {	//按边长由小到大排序
	return a.len < b.len;
}
void ini() {	//初始化
	scanf("%d%d", &n, &m);
	for (int i = 1; i <= m; ++ i)
		scanf("%d%d%d", &Edge[i].a, &Edge[i].b, &Edge[i].len);
	for (int i = 1; i <= n; ++ i)Father[i] = i;	//初始化并查集
	sort(Edge + 1, Edge + m + 1, cmp);
}
int GetFather(int x) {	//并查集，用于判断2个顶点是否属于同一个生成树
	if (x != Father[x])Father[x] = GetFather(Father[x]);
}
void Kruskal() {
	int x, y, k, Cnt, tot;	//k为当前边的编号，tot统计最小生成树的边权总和
	Cnt = 0;	//Cnt统计进行了几次合并，n - 1次合并就得到最小生成树
	k = 0;
	tot = 0;
	while (Cnt < n - 1) {	//n个点构成的生成树只有n - 1条边
		++ k;
		x = GetFather(Edge[k].a);
		y = GetFather(Edge[k].b);
		if (x != y) {
			Father[x] = y;	//合并到一个生成树
			tot += Edge[k].len;
			++ Cnt;
		}
	}
	printf("%d", tot);
}
int main() {
	ini();
	Kruskal();
	return 0;
}

Prim

Prim算法的基本思想：

任选一个点，加入生成树集合。

在未加入生成树的点中，找出离生成树距离最近的一个点，将其加入生成树。

反复上述操作，直到所有点都加入了生成树。

总时间复杂度O(n^2)，其中n为点的个数

以下给出Prim函数代码：

void Prim(int x) {	//开始时任选一点x加入生成树，故一开始树中只有一个点x
	int i, j, k, Min;
	int Dis[103], Path[103];
	for (i = 1; i <= n; ++ i) {
		Dis[i] = Map[i][x];
		Path[i] = x;
	}
	for (i = 1; i <= n - 1; ++ i) {
		Min = inf;
		for (j = 1; j <= n; j += )
			if ((Dis[j] != 0) && (Dis[j] < Min) {
				Min = Dis[j];
				k = j;
		}
		Dis[k] = 0;
		for (j = 1; j <= n; ++ j)
			if( Dis[j] > Map[j][k]) {
				Dis[j] = Map[j][k];
				Path[j] = k;
			}
	}
}