UVA - 1643 Angle and Squares （角度和正方形）（几何）

题意：第一象限里有一个角，把n(n <= 10)个给定边长的正方形摆在这个角里（角度任意），使得阴影部分面积尽量大。

分析：当n个正方形的对角线在一条直线上时，阴影部分面积最大。

1、通过给定的xa,ya,xb,yb，可求k1,k2。

2、当n个正方形的对角线在一条直线上时，设A(x1,k1*x1),B(x2,k2*x2)，

可列方程组：

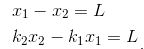
解得

3、利用叉积算出AOB的面积，再减去正方形面积和的一半。

#pragma comment(linker, "/STACK:102400000, 102400000")
#include<cstdio>
#include<cstring>
#include<cstdlib>
#include<cctype>
#include<cmath>
#include<iostream>
#include<sstream>
#include<iterator>
#include<algorithm>
#include<string>
#include<vector>
#include<set>
#include<map>
#include<stack>
#include<deque>
#include<queue>
#include<list>
#define Min(a, b) ((a < b) ? a : b)
#define Max(a, b) ((a < b) ? b : a)
const double eps = 1e-8;
inline int dcmp(double a, double b) {
    if(fabs(a - b) < eps)  return 0;
    return a < b ? -1 : 1;
}
typedef long long LL;
typedef unsigned long long ULL;
const int INT_INF = 0x3f3f3f3f;
const int INT_M_INF = 0x7f7f7f7f;
const LL LL_INF = 0x3f3f3f3f3f3f3f3f;
const LL LL_M_INF = 0x7f7f7f7f7f7f7f7f;
const int dr[] = {0, 0, -1, 1, -1, -1, 1, 1};
const int dc[] = {-1, 1, 0, 0, -1, 1, -1, 1};
const int MOD = 1e9 + 7;
const double pi = acos(-1.0);
const int MAXN = 1000 + 10;
const int MAXT = 10000 + 10;
using namespace std;
struct Point{
    double x, y;
    void set(double xx, double yy){
        x = xx;
        y = yy;
    }
};
double getArea(Point &A, Point &B){
    return A.x * B.y - A.y * B.x;
}
int main(){
    int N;
    while(scanf("%d", &N) == 1){
        if(!N) return 0;
        Point A, B;
        scanf("%lf%lf%lf%lf", &A.x, &A.y, &B.x, &B.y);
        double L = 0;
        double area = 0;
        for(int i = 0; i < N; ++i){
            double l;
            scanf("%lf", &l);
            L += l;
            area += l * l / 2;
        }
        double k1 = A.y / A.x;
        double k2 = B.y / B.x;
        if(k1 > k2){
            swap(k1, k2);
        }
        double x1 = (k2 + 1) * L / (k2 - k1);
        double y1 = k1 * x1;
        double x2 = (k1 + 1) * L / (k2 - k1);
        double y2 = k2 * x2;
        A.set(x1, y1);
        B.set(x2, y2);
        double ans = getArea(A, B) / 2 - area;
        printf("%.3lf\n", ans);
    }
    return 0;
}