KMP算法复杂度证明

引言

KMP算法应该是看了一次又一次，比赛的时候字符串不是我负责，所以学到的东西又还给网上的博客了……

退役后再翻开看，看到模板，心想这不是\(O(n^2)\)的复杂度吗？

有两个循环也不能看做是\(O(n^2)​\)的，这要用到摊还分析．

模板

这里用到的模板是算竞上的

• calc_next()

    Next[1] = 0;
    for (int i = 2, j = 0; i <= n; ++i) {
        while (j > 0 && a[i] != a[j + 1]) j = Next[j];
        if (a[i] == a[j + 1]) ++j;
        Next[i] = j;
    }

• kmp()

   for (int i = 1, j = 0; i <= m; ++i) {
        while (j > 0 && (j == n || b[i] != a[j + 1]))j = Next[j];
        if (b[i] == a[j + 1])++j;
        f[i] = j;
    }

可以发现上下两个函数挺像的，Next[i]含义就是模式串以\(i\)结尾的子串([1..i]的后缀)与模式串的前缀能匹配的最长长度

证明

观察发现有两个操作:

• 匹配成功：j++,这个代价是1
• 匹配失败: j=Next[j]还要经过while循环，这个代价未知

根据记账法，假设每个平摊代价是2,对于每个匹配成功的操作，其中1元用来j++，另1元就存起来，给后面匹配失败时用:

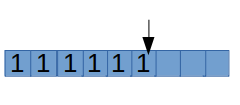
而当失配的时候，就会用到银行存款，最坏的情况当然就是用光了所有存款，但可以发现每个匹配的操作分配两个时间代价是完全足够的

换句话说，你使用存款肯定得要求银行有存款，而每次j++操作都会存1元，在当前j前面必然每个位置都是有大于等于1的存款

所以复杂度就是j++次数的两倍，也就是匹配串的长度 \(2n\)

根据平摊分析要求\(\check c_i \ge c_i\)，平摊代价设置为\(2\)是完全满足的

综上所述:KMP算法两个函数的总体运算次数为\(2n+2m\)，复杂度是\(O(n+m)\)

总结

也不知道这样分析对不对，如果只是感性理解的话足够了．

也有势能法的做法，但是这样的话就要定义势能函数，我觉得记账法还是好理解一点.