吴恩达老师机器学习课程chapter04——神经网络

本文是非计算机专业新手的自学笔记，高手勿喷，欢迎指正与其他任何合理交流。

本文仅作速查备忘之用，对应吴恩达(AndrewNg)老师的机器学期课程第八章、第九章。

吴恩达老师机器学习课程chapter04——神经网络

二分类

基本概念

对于复杂的非线性分类问题，线性回归中构造非线性的多项式回归可能会变得十分复杂，特征数会变得很多。

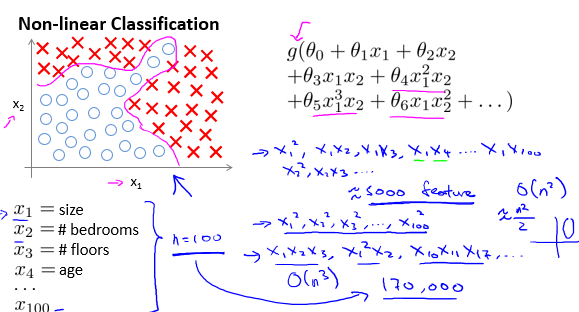
这种情况下，可以使用神经网络。神经网络运用简单的数学模型模拟人脑中神经元的工作方式。如图是一个简单的神经元模型：

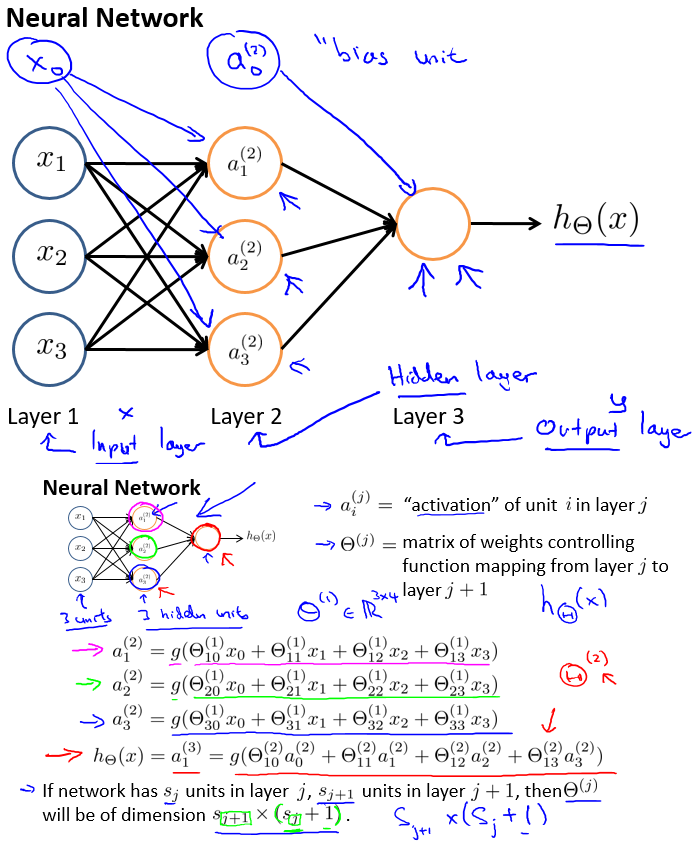
其中有三层：输入层(layer 1: input layer)，隐藏层(layer 2: hidden layer)，输出层(layer 3: output layer)。

常常添加x0、a0，来构成常数偏置项。

$ a_{i}^{(j)} $ 表示第j层激活项，由输入层经过某种函数计算得到，这个函数也叫做激活函数。

分类问题中的Sigmoid函数，被用作一种激活函数。

实质上是从现有特征中，学到的新的特征的过程。
$ \Theta ^{(j)} $ 表示由系数θ构成的、（$s_{j+1}\times s_{j}+1$）的系数矩阵，从第j层指向第j+1层。

由输入层到隐藏层到输出层，这样的传播被称为神经网络的前向传播(forward propogation)过程。

写作矩阵形式：

\[\Theta g(x^{(1)})=g(z^{(2)})=a^{(2)\prime}
\]

其中，$x^{(1)\prime}$不含偏置项$x^{(1)}_0$，补上常数偏置项得$x^{(1)}$，$a^{(2)\prime}$不含偏置项$a^{(2)}_0$，补上常数偏置项得$a^{(2)}$

神经网络的层数可以灵活增加，以获取更复杂的特征。

简单举例

神经网络实现AND逻辑

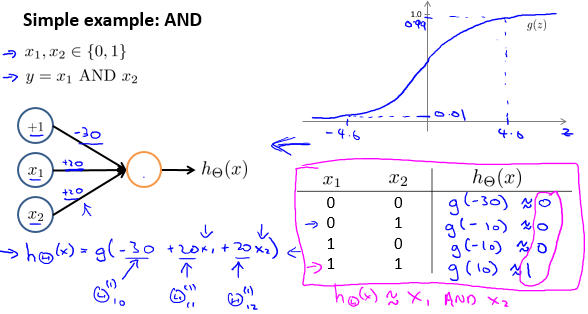
神经网络实现OR逻辑

神经网络实现NOT逻辑

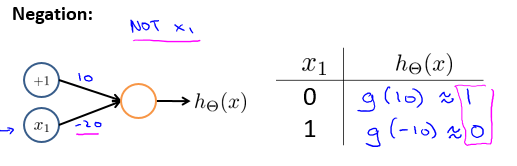
神经网络实现NOR逻辑

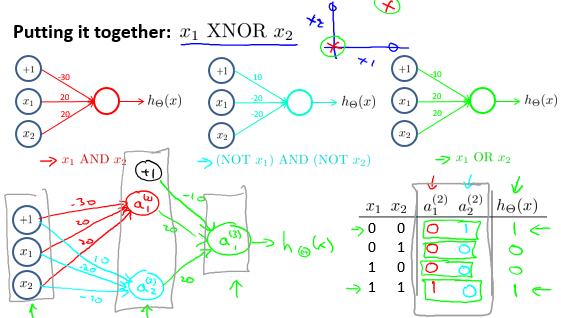
多分类

以上举例实现的是二分类问题。想要实现多分类。本质上就是拓展输出层。

输出层不再是一个数，而是一组由概率构成的向量。选取概率最大作为输出结果。

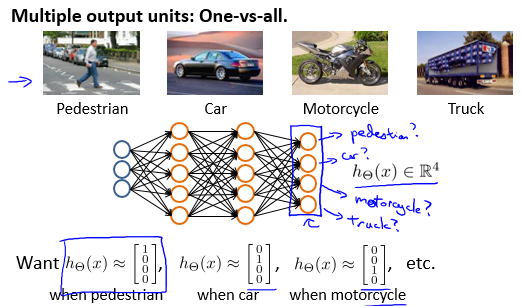
这种时候输出写为$h_{\Theta}(x) \in \mathbb{R}^{K} $，是一个K维向量，有K个可能的输出结果。

$\quad\left(h_{\Theta}(x)\right)_{i}=i^{t h} \text { output }$。

代价函数

神经网络的代价函数为：

\[\begin{aligned}
J(\Theta)=&-\frac{1}{m}\left[
\sum_{i=1}^{m} \sum_{k=1}^{K} y_{k}^{(i)} \log \left(h_{\Theta}\left(x^{(i)}\right)\right)_{k}+\left(1-y_{k}^{(i)}\right) \log \left(1-\left(h_{\Theta}\left(x^{(i)}\right)\right)_{k}\right)\right] \\
&+\frac{\lambda}{2 m} \sum_{l=1}^{L-1} \sum_{i=1}^{s_{l}} \sum_{j=1}^{s_{l+1}}\left(\Theta_{j i}^{(l)}\right)^{2}
\end{aligned}
\]

其构成有两部分组成：

1. 由m个训练样本的Cost函数之和

2. 正则项

更新系数——反向传播(back-propogation)

运用梯度下降法解最优问题，会遇到求偏导数$\frac{\partial J(\Theta )}{\partial \Theta ^{(l)}_{ij}} $的问题：

其思想请直接参考博客https://blog.csdn.net/weixin_38347387/article/details/82936585

其实质依然是偏微分的链式求导法则。

其结果为：

这里暂不做详细推导。