运筹学笔记12 大M法



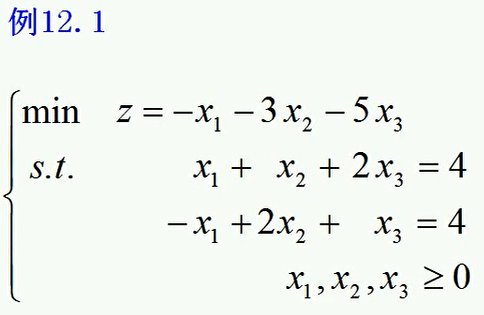

引入M,其中M是一个充分大的正数。由此,目标函数也改变为zM.
如此构造的线性规划问题我们记作LPM,称之为辅助线性规划问题,也即在原来的线性规划问题的基础上,改造了其等式约束条件,然后有对目标函数施加了惩罚项,Mx4,Mx5。
因为M是充分大的正数,所以即便x4,x5很小,只要x4,x5不等于0,这个惩罚项也也会很大的;一旦大M趋于正无穷,那么Mx4,Mx5一块就是正无穷了;而前面的各变量及其系数
的组合也是有限的量;根据一个有限的量加上一个无穷大量结果是无穷大量定理;那么目标函数就是趋于无穷大量,怎么还会取得最小值呢?∴大M叫做惩罚项是有道理的,而且
在理想的状态下,一旦x4,x5取值为零,那么目标函数中就再也没有惩罚项了,目标函数也就有zM还原为z了,同时约束条件x4,x5也就消失了,因为二者此时为零;
这样也就实现了有LPM向原线性规划问题的还原。所以大M法,首先引入大M惩罚项,对人为引入的人工变量施加惩罚,最佳的状态就是把引入的人工变量都惩罚为0,这样不仅等式约束条件没被破坏,目标函数也还原为原来的目标函数了。如果做不到这一步,就说明有些约束条件原来就不可能相等。
我们构造辅助线性规划问题后可看到已经有x4,x5系数组成的单位矩阵了,我们把它取作初始可行基。

进而可以写出典式的等价形式(把基变量和目标函数都用非基变量表示)如下:

进而做出单纯形表:

有了单纯形表,进一步讨论三种情形。
情形1:是否全部的检验数都<=0;很显然此题不是;1肯定是>0的,另外M是充分大的正数所以3M+3,3M+5也都是>=0的。
情形2:正的检验数上面没有正的,才是第二种情况;此题不符合;
显然是第三种情况了,选定枢轴列->元,然后转轴。

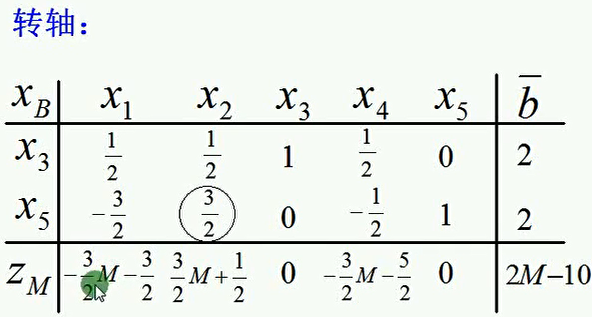
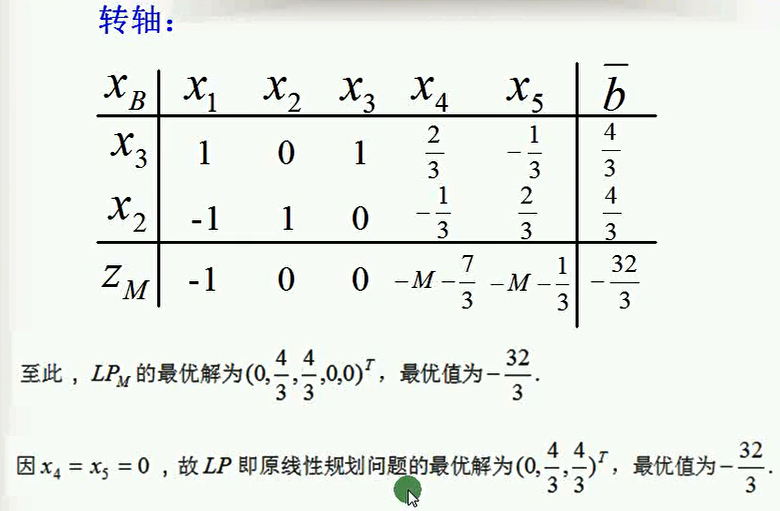
上图得到了辅助线性规划问题的最优解和最优值,但须注意,在辅助线性规划问题中,我们引入了两个人工变量的值,x4,x5,
也可发现在LPM的最优解中两个变量都已经为0了。也即是说,辅助线性规划的人工变量都已经被充分大的大M构造的惩罚项惩罚为0了,也就是说又还原为原来初始的线性规划问题了,所以据此我们就可以得到LP,即原来线性规划问题的最优解和最优值。。。
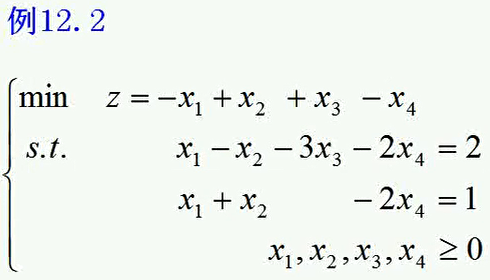




可看到上图中有一个检验数是正的,其所在列上面的值都是<=0,所以是第二种情形,所以LPM无下届。
而之前引入的人工变量x5对应的取值为1,并没有被惩罚为0;另一个非基变量x6作为非基变量已经被惩罚为0了;
也即,因x5=1,x6=0,故原线性规划问题不可行。

练习:
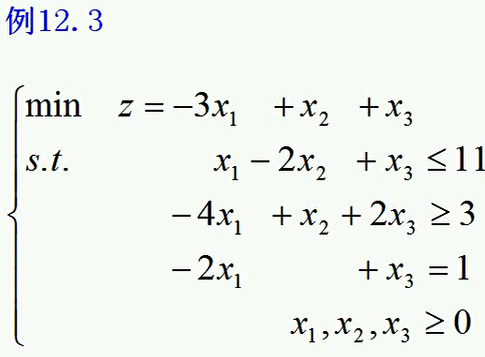
运筹学笔记12 大M法的更多相关文章
- SQL反模式学习笔记12 存储图片或其他多媒体大文件
目标:存储图片或其他多媒体大文件 反模式:图片存储在数据库外的文件系统中,数据库表中存储文件的对应的路径和名称. 缺点: 1.文件不支持Delete操作.使用SQL语句删除一条记录时,对应的文 ...
- 大M法(Big M Method)
前面一篇讲的单纯形方法的实现,但程序输入的必须是已经有初始基本可行解的单纯形表. 但实际问题中很少有现成的基本可行解,比如以下这个问题: min f(x) = –3x1 +x2 + x3 s.t. x ...
- 机器学习实战 - 读书笔记(12) - 使用FP-growth算法来高效发现频繁项集
前言 最近在看Peter Harrington写的"机器学习实战",这是我的学习心得,这次是第12章 - 使用FP-growth算法来高效发现频繁项集. 基本概念 FP-growt ...
- JAVA自学笔记12
JAVA自学笔记12 1.Scanner 1)JDK5后用于获取用户的键盘输入 2)构造方法:public Scanner(InputStream source) 3)System.in 标准的输入流 ...
- 大津法---OTSU算法
简介: 大津法(OTSU)是一种确定图像二值化分割阈值的算法,由日本学者大津于1979年提出.从大津法的原理上来讲,该方法又称作最大类间方差法,因为按照大津法求得的阈值进行图像二值化分割后,前景与背景 ...
- 自适应阈值分割—大津法(OTSU算法)C++实现
大津法是一种图像灰度自适应的阈值分割算法,是1979年由日本学者大津提出,并由他的名字命名的.大津法按照图像上灰度值的分布,将图像分成背景和前景两部分看待,前景就是我们要按照阈值分割出来的部分.背景和 ...
- matlab学习笔记12单元数组和元胞数组 cell,celldisp,iscell,isa,deal,cellfun,num2cell,size
一起来学matlab-matlab学习笔记12 12_1 单元数组和元胞数组 cell array --cell,celldisp,iscell,isa,deal,cellfun,num2cell,s ...
- Ext.Net学习笔记12:Ext.Net GridPanel Filter用法
Ext.Net学习笔记12:Ext.Net GridPanel Filter用法 Ext.Net GridPanel的用法在上一篇中已经介绍过,这篇笔记讲介绍Filter的用法. Filter是用来过 ...
- 自适应阈值二值化之最大类间方差法(大津法,OTSU)
最大类间方差法是由日本学者大津(Nobuyuki Otsu)于1979年提出的,是一种自适应的阈值确定的方法,又叫大津法,简称OTSU.它是按图像的灰度特性,将图像分成背景和目标2部分.背景和目标之间 ...
随机推荐
- js new Date()参数格式
最近在写页面使用new Date()获取时间戳在ie浏览器中测试发现无效:后来发现是参数格式问题, new Date()参数格式如下: 1.用整数初始化日期对象 var date1 = new Dat ...
- MVVM模式-数据的双向绑定
- socket套接字模块及黏包现象
一.socket套接字模块 socket概念 socket层 理解socket Socket是应用层与TCP/IP协议族通信的中间软件抽象层,它是一组接口.在设计模式中,Socket其实就是一个门面模 ...
- ArcGIS使用技巧(七)——批量导出
新手,若有错误还请指正! 在ArcGIS中如何将栅格数据批量导出?用到"复制栅格这个工具",这里我用的例子是:将ArcGIS默认输出的DEM文件夹批量导出为tif格式.(如果是文件 ...
- SpringCloud入门简述
1.微服务简述 微服务,是一个小型的服务,也是一种设计理念,将一个大型繁杂的系统拆分为多个小型的服务,进行独立部署,这些服务在独立进程中运行,通过特定的协议进行通信 优点: 轻量化:一个服务不 ...
- 如何离线安装posh-git
不用上github 1.下载post-git离线安装包 地址:https://files.cnblogs.com/files/xcr1234/posh-git-master.zip 2,用Powers ...
- 修改本地仓库Maven,设置镜像
修改本地仓库的位置: 先建立 文件路径: 进入文件夹目录: 就可以看到一个配置文件夹 就在里面修改本地仓库的路径,设置阿里云镜像 添加本地阿里云镜像: 如下图: 内容如下: <mirror> ...
- 聊聊FLINK-25631贡献
从入行做数据库开发,到2018年过渡到大数据开发,可以说我已经与sql朝夕相处了七八年了,经常惊讶于简单的语法就能产生复杂的操作,而且还能根据索引等统计信息自动优化,不禁很想实现自己的sql语法,却不 ...
- Java 17 新特性:switch的模式匹配(Preview)
还记得Java 16中的instanceof增强吗? 通过下面这个例子再回忆一下: Map<String, Object> data = new HashMap<>(); da ...
- Centos7部署Redis集群
Redis简介 Redis(Remote Dictionary Server)是完全开源的.遵守BSD协议的.高性能的Key-Value数据库. Redis与其他Key-Value缓存产品有一下三个特 ...
