.Net CLR GC plan_phase二叉树和Brick_table

楔子

别那么懒，勤快点。以下取自CLR PreView 7.0。

主题

GC计划阶段(plan_phase)主要就两个部分，一个是堆里面的对象构建一颗二叉树（这颗二叉树的每个节点包含了诸如对象移动信息等等，此处不述）。但是，这个二叉树如果过于庞大（对象太多的情况），则成了性能瓶颈（从根节点遍历需要查找的节点的空间和时间复杂度）。于是乎，第二个部分Brick_table出现了，它主要是分割这个庞大的二叉树，以消弭性能瓶颈问题。

构建不规则二叉树

构建二叉树之前，先了解一些概念。当实例化一个对象之后，这个对象存储在堆里面。堆实际上是一长串的内存地址，不受CPU栈的管控，所以导致了它不能自动释放，需要手动。在这一长串的地址里面，可以分为固定对象和非固定对象。

1.固定对象概念

首先看下固定句柄，固定句柄就是把托管对象地址传递到非托管对象的堆栈里面去，固定句柄本身在托管里面进行管理，而它包含的对象就叫做固定对象。

至于非固定对象，就是普通的对象了，此处不再赘述。

在进行GC计划阶段的时候，会循环遍历当前需要收集的垃圾的代（generation）里面包含的所有堆,然后区分出包含固定对象的堆段，和非固定对象的堆段。

区分规则是怎么样的呢？具体的就是如果相邻的两个对象都是非固定对象或者都是固定对象，则把这两个对象作为一个堆段，继续查找后面的对象。如果后续的对象跟前面的对象相同，则跟前面的两个对象放在一起形成一个堆段（如果后面还有相同的，则继续放在一起），如果不同，则此堆段到此为止。后面继续以同样的逻辑遍历，形成一个个的小堆段（以node表述）。

2.这里有一个特性：

固定堆段（也就是固定对象组成的堆段）的末尾必须跟一个非固定对象（这么做的原因，是避免固定对象的末尾被覆盖，只覆盖非固定对象的末尾）。

二叉树的构建，就建立在这些固定对象堆段和非固定对象堆段上的。这些一个个的堆段作为二叉树的根节点和叶子结点，构成了二叉树的本身。

3.相关构建

一：plug_and_pair结构

plug_and_pair存在于上面被分割的堆段的前面，堆段以node(节点)表示，则此结构(plug_and_pair*)node)[-1]的位置

struct plug
{
    uint8_t *  skew[plug_skew / sizeof(uint8_t *)];
};

class pair
{
  public:
    short left;
    short right;
};
struct plug_and_pair
{
    pair        m_pair;
    plug        m_plug;
};

pair的left和right成员分别表示当前堆段距离其前一个堆段和后一个堆段的距离长度。

二：构建逻辑

构建逻辑分为三种，数字一般可以分为奇数和偶数。计算机也是一样，但是除了这两种之外，偶数里面还可以分裂出另外一种情况，就是一个数字是2的次方数。举个例子，比如： 1,2,3,4,5,6,7,8,9,10。这十个数字里面，明显的奇数：1,3,5,7,9。偶数：2,4,6,8,10。再分裂下二的次方数：2,4,8。注意看，最后分裂的结果2,4,8分别是2的1次方，2次方和3次方。剔除了6和10这两个数字。

那么总结下，三种逻辑以上面试个数字举例分别为：

遍历循环以上十个数字。

第一种(if(true))：1,2,4,8 if(!(n&(n-1))) n分别为2,4,8。if里为true

第二种(if(true))：3,5,7,9 if(n&1) n分别为1,3,5,7,9。if里为true

第三种(if(true))：6,10 如果以上两种不成立，则到第三种这里来。

三：构建树身

如上所述，通过对堆里面的对象进行固定和非固定对象区分，变成一个个的小堆段(node)。这些小堆段从左至右依次编号：1,2,3,4,5,6,7,8,9.......N。然后通过构建逻辑这部分进入到if里面去。

1.(if(true))：

1,2,4,8编号的node会进入这里，主要是设置左节点和tree
set_node_left_child (new_node, (tree - new_node));
 tree = new_node;

2.(if(true))：

3,5,7,9编号的node会进入这里，主要是设置右节点
set_node_right_child (last_node, (new_node - last_node));

3.(if(true))：

            6,10编号的会进入这里，主要是把原来的二叉树的右子节点变成新的node(new_node)的左子节点，
            切断二叉树与它自己右子节点的联系。然后把新的node(new_node）,变成原来二叉树的右子节点。
            uint8_t*  earlier_node = tree;
            size_t imax = logcount(sequence_number) - 2;//这里是获取需要变成的二叉树的右子树节点的层级。
            for (size_t i = 0; i != imax; i++)//如果层级不等于0，则获取到二叉树根节点到右子节点的距离，然后把根节点与右子节点相加得到二叉树右子节点。如此循环遍历，到二叉树最底层的右子节点为止。
            {
                earlier_node = earlier_node + node_right_child (earlier_node);
            }
	    获取到最后一颗二叉树的根节点的右子树的距离
            int tmp_offset = node_right_child (earlier_node);
            assert (tmp_offset); // should never be empty
	    把最后一颗二叉树的根节点和最后一颗二叉树的右子节点相加，设置为新的node(new_node)的左子树。
            set_node_left_child (new_node, ((earlier_node + tmp_offset ) - new_node));
	    把最后一颗二叉树的右子树节点设置为新的node(new_node)节点，同时也是断了开与原来右子树的联系。
            set_node_right_child (earlier_node, (new_node - earlier_node));

GC plan_phase的二叉树构建本身并不复杂，而是复杂的逻辑和诡异的思维方式。

最终的构建的二叉树形式如下图所示：

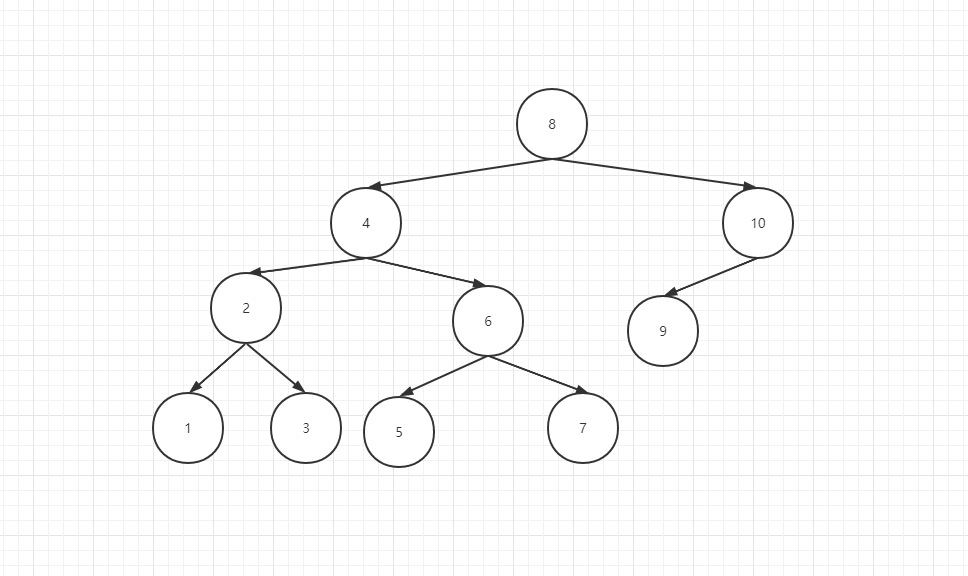
四.分割二叉树

当以上二叉树被构建之后，如有几千个节点（node,小堆段）会形成庞大的一棵树。所以需要分割功能，用以来保证性能。

当二叉树包含的小堆段（node）的长度超过2的12次方（4kb），这棵二叉树就会被分割。

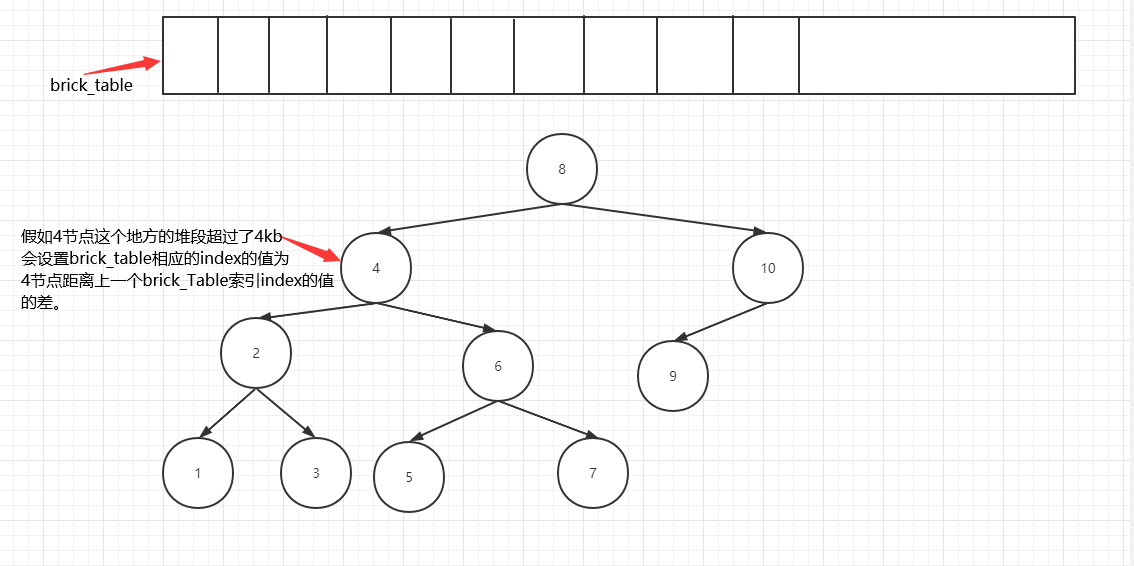
Brick_table里面属于这个4节点范围内的都是赋值为-1，表示你要在4节点上寻找你需要的节点。

源码：

最后上一下源码

1.构建二叉树：

uint8_t* gc_heap::insert_node (uint8_t* new_node, size_t sequence_number,
                   uint8_t* tree, uint8_t* last_node)
{
    dprintf (3, ("IN: %Ix(%Ix), T: %Ix(%Ix), L: %Ix(%Ix) [%Ix]",
                 (size_t)new_node, brick_of(new_node),
                 (size_t)tree, brick_of(tree),
                 (size_t)last_node, brick_of(last_node),
                 sequence_number));
    if (power_of_two_p (sequence_number))
    {
        set_node_left_child (new_node, (tree - new_node));
        dprintf (3, ("NT: %Ix, LC->%Ix", (size_t)new_node, (tree - new_node)));
        tree = new_node;
    }
    else
    {
        if (oddp (sequence_number))
        {
            set_node_right_child (last_node, (new_node - last_node));
            dprintf (3, ("%Ix RC->%Ix", last_node, (new_node - last_node)));
        }
        else
        {
            uint8_t*  earlier_node = tree;
            size_t imax = logcount(sequence_number) - 2;
            for (size_t i = 0; i != imax; i++)
            {
                earlier_node = earlier_node + node_right_child (earlier_node);
            }
            int tmp_offset = node_right_child (earlier_node);
            assert (tmp_offset); // should never be empty
            set_node_left_child (new_node, ((earlier_node + tmp_offset ) - new_node));
            set_node_right_child (earlier_node, (new_node - earlier_node));

            dprintf (3, ("%Ix LC->%Ix, %Ix RC->%Ix",
                new_node, ((earlier_node + tmp_offset ) - new_node),
                earlier_node, (new_node - earlier_node)));
        }
    }
    return tree;
}

2.切割二叉树：

size_t gc_heap::update_brick_table (uint8_t* tree, size_t current_brick,
                                    uint8_t* x, uint8_t* plug_end)
{
    dprintf (3, ("tree: %Ix, current b: %Ix, x: %Ix, plug_end: %Ix",
        tree, current_brick, x, plug_end));

    if (tree != NULL)
    {
        dprintf (3, ("b- %Ix->%Ix pointing to tree %Ix",
            current_brick, (size_t)(tree - brick_address (current_brick)), tree));
        set_brick (current_brick, (tree - brick_address (current_brick)));//brick_table索引处的值是：根节点tree距离当前current_brick对应的地址的距离
    }
    else
    {
        dprintf (3, ("b- %Ix->-1", current_brick));
        set_brick (current_brick, -1);
    }
    size_t  b = 1 + current_brick;
    ptrdiff_t  offset = 0;
    size_t last_br = brick_of (plug_end-1);//上一个plug节点的末尾
    current_brick = brick_of (x-1);//当前的plug_start
    dprintf (3, ("ubt: %Ix->%Ix]->%Ix]", b, last_br, current_brick));
    while (b <= current_brick)
    {
        if (b <= last_br)
        {
            set_brick (b, --offset);
        }
        else
        {
            set_brick (b,-1);
        }
        b++;
    }
    return brick_of (x);
}

以上参考：

https://github.com/dotnet/coreclr/blob/main/src/gc/gc.cpp