leetcode二叉树题目总结

leetcode二叉树题目总结

题目链接：https://leetcode-cn.com/leetbook/detail/data-structure-binary-tree/

前序遍历(NLR)

• public List<Integer> preorderTraversal(TreeNode root) {
      List<Integer> res = new ArrayList<>();
      preOrder(root, res);
      return res;
  }
  ​
  public void preOrder(TreeNode root, List<Integer> res) {
      if (root == null)
          return;
      res.add(root.val);
      preOrder(root.left, res);
      preOrder(root.right, res);
  }

中序遍历（LNR）

• inOrder(root.left, res);
  res.add(root.val);
  inOrder(root.right, res);

后序遍历( LRN )

• postOrder(root.left, res); 
  postOrder(root.right, res);
  res.add(root.val);

层次遍历

    3
   / \
  9  20
    /  \
   15   7 
结果
[
  [3],
  [9,20],
  [15,7]
]

关键代码

public List<List<Integer>> levelOrder(TreeNode root) {
    // 空树判断
    if(root == null) return result;
    // 返回的结果
    List<List<Integer>> result = new ArrayList<>();
    // 队列
    Queue<TreeNode> queue = new LinkedList<>();
    // 根节点入队
    queue.add(root);
    // 队列不为空则循环
    while(queue.size()>0){
        // 内层节点序列
        List<Integer> temp = new ArrayList<>();
        // 遍历队列,把当前层的元素从队列取出来,将下一层放入队列
        for(int i=0;i<size;i++){
            // 当前节点放入结果数组
            TreeNode cur = queue.poll();
            temp.add(cur);
            // 左节点入队
            if(cur.left){
                queue.add(cur.left);
            }
            // 右节点入队
            if(cur.right){
                queue.add(cur.right)
            }
        }
        result.add(temp);
    }
    return result;
}

二叉树最大深度

递归解决:

• 递归出口 当前节点 == null 返回0

• 递归逻辑 Math.max(maxDept(root.left) +1, maxDepth(root.right) +1)

public int maxDepth(TreeNode root) {
    if(root == null) return 0;
    return Math.max(maxDepth(root.left)+1, maxDepth(root.right)+1);
}

对称二叉树

递归法:

递归出口: 两个节点同时为空 return true 有一个为空 return false

递归逻辑: 返回当前节点值是否相等 && 递归节点1的左节点和节点2的右节点 && 递归节点2的右节点和节点1的左节点

class Solution {
    public boolean isSymmetric(TreeNode root) {
        return isMirror(root, root);
    }
    public boolean isMirror(TreeNode t1, TreeNode t2) {
        if (t1 == null && t2 == null) return true;
        if (t1 == null || t2 == null) return false;
        return (t1.val == t2.val)
                && isMirror(t1.left, t2.right)
                && isMirror(t1.right, t2.left);
    }
}

路径总和

递归法: 递归出口: 当前节点==null判断 当前的 target是否为0,是则返回true,否返回false

递归逻辑: DFS所有节点,每次遍历到当前节点将target-cur.val

class Solution {
    public boolean hasPathSum(TreeNode root, int targetSum){
        // 处理root为空的情况
        if(root == null){
             return false;
        }
        // 叶子节点判定当前路径是否可行
        if(root.left==null && root.right==null){
            return root.val == targetSum;
        }
        return hasPathSum(root.left,targetSum-root.val) || hasPathSum(root.right,targetSum-root.val);
    }
}

中序后序构造二叉树

思路:

• 通过后序遍历确定每一个根节点

• 通过DFS递归,限定范围得到左右子树

• 递归出口 后序遍历的head > tail

• 通过找到当前节点在中序遍历中的位置限定范围

class Solution {
    public TreeNode buildTree(int[] inorder, int[] postorder) {
        int len=inorder.length;
        if(len==0)return null;
        return dfs(inorder,postorder,0,len-1,0,len-1);
    }
​
    TreeNode dfs(int[] inorder, int[] postorder,int head1,int tail1, int head2,int tail2){
        // 由于postOrder每次都会在tail-1 所以当只有一个元素则会返回
        if(head2>tail2)return null;

        int val=postorder[tail2];
        TreeNode root=new TreeNode(val);
        if(head2==tail2)return root;
​
        int mid=0;  //拆分点mid的位置是相对的，因为h1!=h2
        while(inorder[head1+mid]!=val)mid++;
​
        root.left=dfs(inorder, postorder, head1, head1+mid-1, head2, head2+mid-1);
        root.right=dfs(inorder, postorder, head1+mid+1, tail1, head2+mid, tail2-1);
​
        return root;
    }
}

笔记：

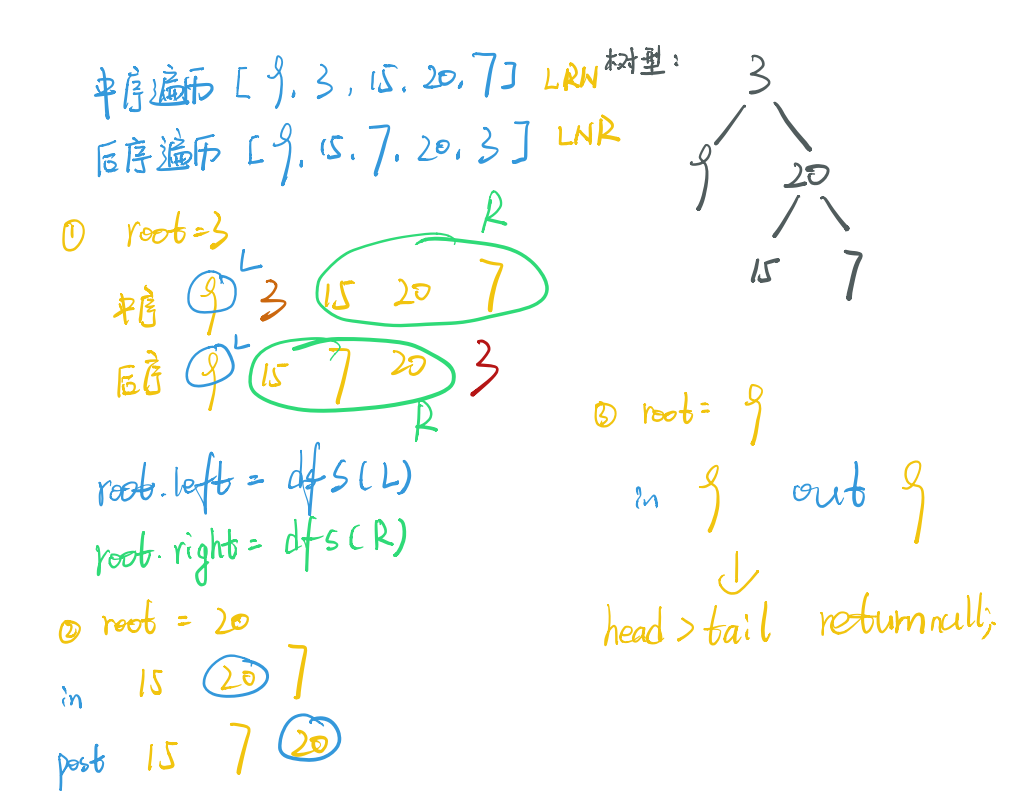
前序中序构造二叉树类似

和中序前序类似, 只是每次的限定范围不同

二叉树填充右侧指针

递归法: 限定完美二叉树

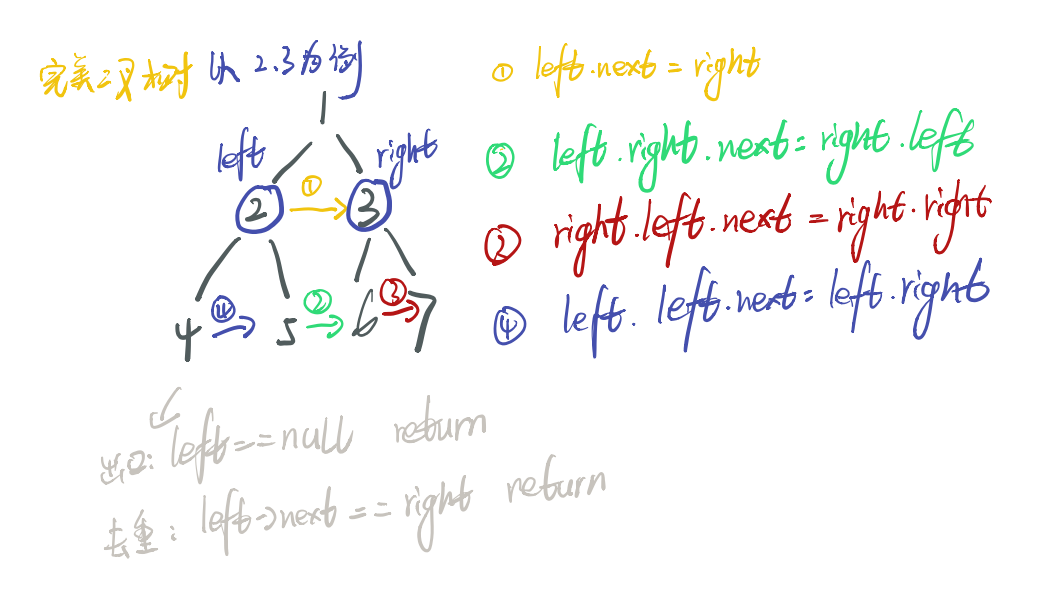
class Solution {
    public Node connect(Node root){
        if(root!=null) dfs(root.left, root.right);
        return root;
    }
    void dfs(Node left, Node right){
        if(left ==null || left.next == right) return;
        left-> next = right;
        dfs(left.left, left.right);
        dfs(left.right, right.left);
        dfs(right.left, right.right);
    }
}

一般情况

/*
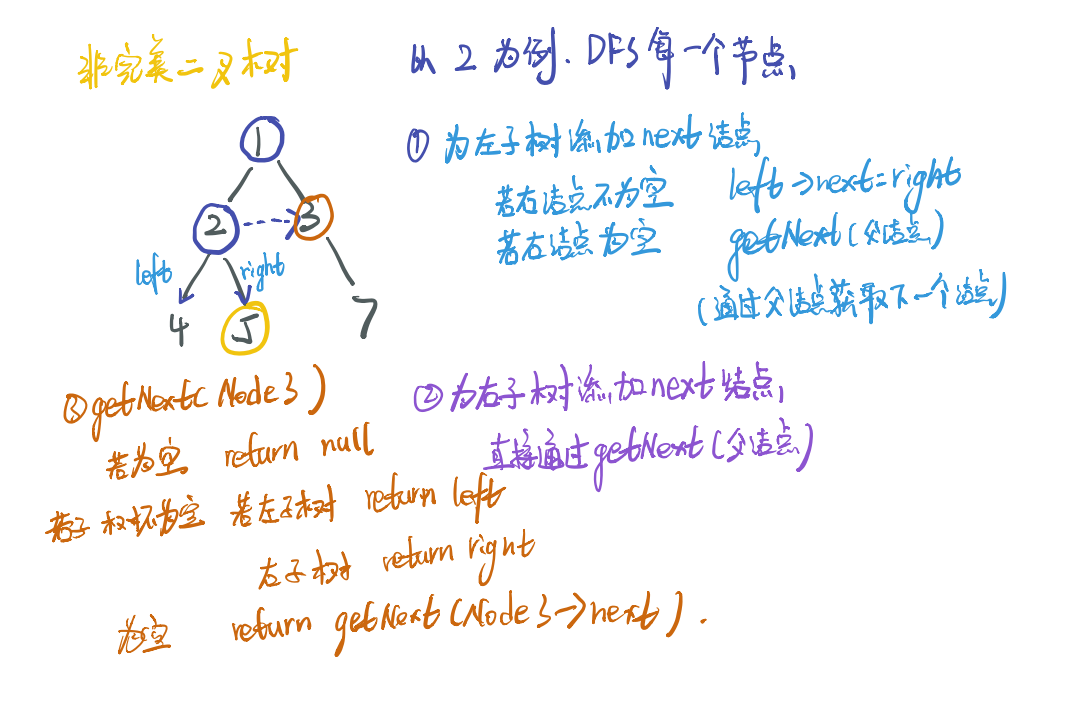
// Definition for a Node.
class Node {
public:
    int val;
    Node* left;
    Node* right;
    Node* next;
​
    Node() : val(0), left(NULL), right(NULL), next(NULL) {}
​
    Node(int _val) : val(_val), left(NULL), right(NULL), next(NULL) {}
​
    Node(int _val, Node* _left, Node* _right, Node* _next)
        : val(_val), left(_left), right(_right), next(_next) {}
};
*/
​
class Solution {
public:
    Node* connect(Node* root) {
        // 空树判断
        if( root == nullptr ) return nullptr;
        // 左树为空
        if( root -> left != nullptr ) {
            if( root -> right != nullptr){
                // 最普遍的情况
                root -> left -> next = root -> right;
            }
            else
                // 父节点的next的第一个子节点作为next
                root -> left -> next = getNext(root -> next);
        }
        // 右节点不为空
        if( root->right != nullptr){
            // next
            root -> right -> next = getNext( root-> next );
        }
        // 先判断右节点
        connect(root->right);
        connect(root->left);
​
        return root;
    }
    // 通过父节点获取子节点的next结点
    Node* getNext(Node* uncle){

        if( uncle == nullptr ) return nullptr;

        if( uncle -> left != nullptr) return uncle->left;

        if( uncle -> right != nullptr ) return uncle->right;

        return getNext(uncle->next);
    }
};

最近公共祖先

整体思路：1. 通过BFS得到每个节点和其父节点的Map

1. 通过Set，保存p到根节点的路径

2. 在通过获得q到根节点的路径，判断第一个包含在原来的set的节点为最先公共祖先

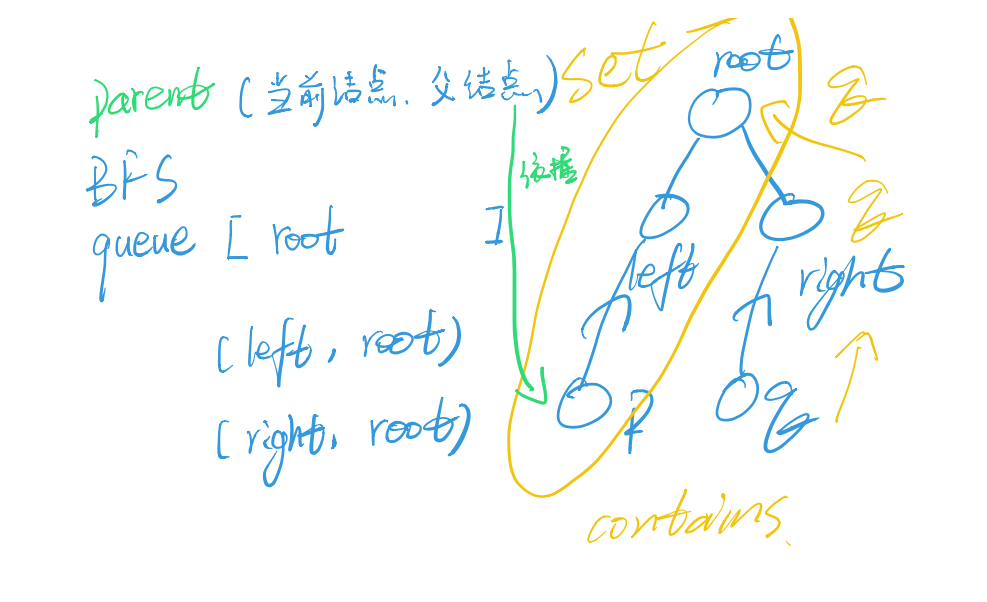
代码：

  public TreeNode lowestCommonAncestor(TreeNode root, TreeNode p, TreeNode q) {

        //记录遍历到的每个节点的父节点。
        Map<TreeNode, TreeNode> parent = new HashMap<>();
        Queue<TreeNode> queue = new LinkedList<>();

        //根节点没有父节点，所以为空
        parent.put(root, null);
        //队列入队
        queue.add(root);

        //直到两个节点都找到为止。
        while (!parent.containsKey(p) || !parent.containsKey(q)) {
            //队列是一边进一边出，这里poll方法是出队，
            TreeNode node = queue.poll();
            if (node.left != null) {
                //左子节点不为空，记录下他的父节点
                parent.put(node.left, node);
                //左子节点不为空，把它加入到队列中
                queue.add(node.left);
            }
            //右节点同上
            if (node.right != null) {
                parent.put(node.right, node);
                queue.add(node.right);
            }
        }
        Set<TreeNode> ancestors = new HashSet<>();
        //记录下p和他的祖先节点，从p节点开始一直到根节点。
        while (p != null) {
            ancestors.add(p);
            p = parent.get(p);
        }
        //查看p和他的祖先节点是否包含q节点，如果不包含再看是否包含q的父节点……
        while (!ancestors.contains(q))
            q = parent.get(q);
        return q;
    }
​

二叉树的序列化和反序列化

分析思路：

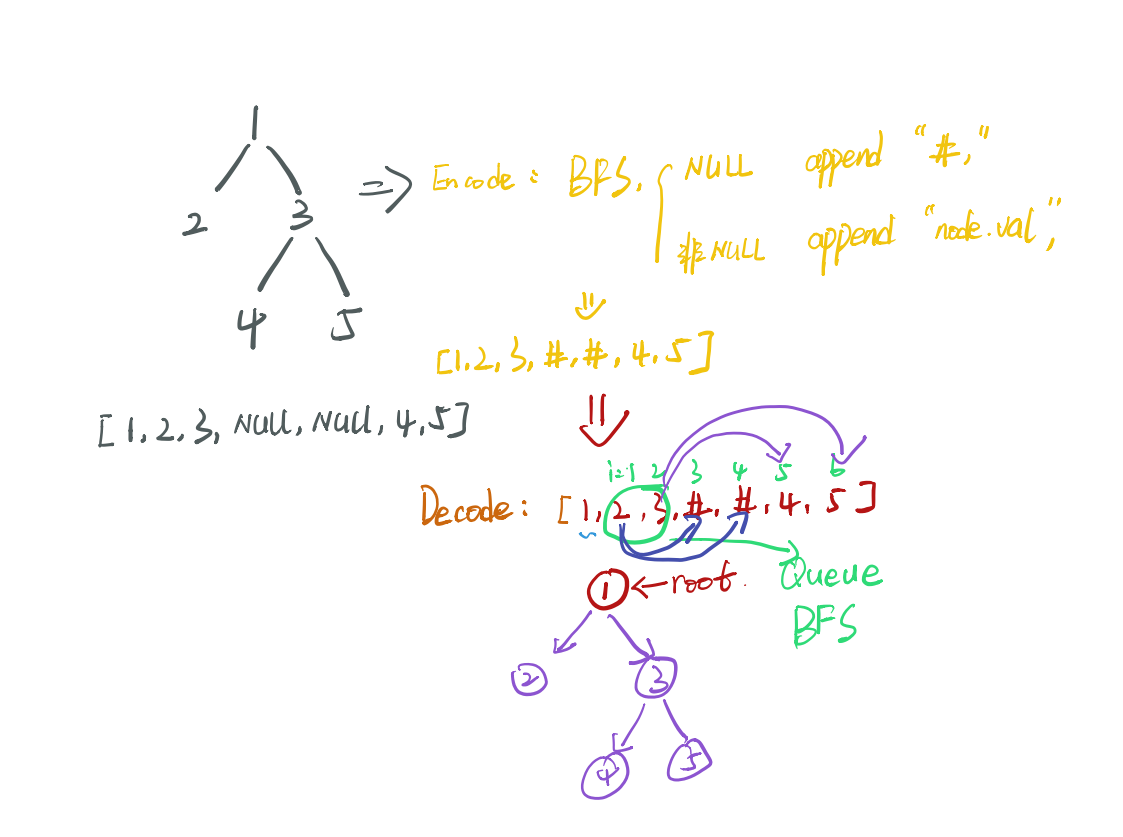
代码：

/**
 * Definition for a binary tree node.
 * public class TreeNode {
 *     int val;
 *     TreeNode left;
 *     TreeNode right;
 *     TreeNode(int x) { val = x; }
 * }
 */
public class Codec {
​
    // Encodes a tree to a single string.
    public String serialize(TreeNode root) {
     if(root == null) return "#";
        Queue<TreeNode> queue = new LinkedList<TreeNode>();
        StringBuffer res = new StringBuffer();
        queue.add(root);
        while(!queue.isEmpty()){
            TreeNode node = queue.poll();
            if(node == null){
                res.append("#,");
                continue;
            }
            res.append(node.val + ",");
            queue.add(node.left);
            queue.add(node.right);
        }
        return res.toString();
    }
​
    // Decodes your encoded data to tree.
    public TreeNode deserialize(String data) {
          if(data == "#") return null;
        Queue<TreeNode> queue = new LinkedList<>();
        String[] values = data.split(",");
        // 第一个节点
        TreeNode node = new TreeNode(Integer.parseInt(values[0]));
        queue.add(node);
        for(int i =1; i < values.length; i++){
            TreeNode treeNode = queue.poll();
            if(!"#".equals(values[i])){
                treeNode.left = new TreeNode(Integer.parseInt(values[i]));
                queue.add(treeNode.left);
            }
            if(!"#".equals(values[++i])){
                treeNode.right = new TreeNode(Integer.parseInt(values[i]));
                queue.add(treeNode.right);
            }
        }
        return node;
    }
}
​
// Your Codec object will be instantiated and called as such:
// Codec ser = new Codec();
// Codec deser = new Codec();
// TreeNode ans = deser.deserialize(ser.serialize(root));