你真的了解 RSA 加密算法吗？

作者：小傅哥

博客：https://bugstack.cn

源码：https://github.com/fuzhengwei/java-algorithms

沉淀、分享、成长，让自己和他人都能有所收获！

记得那是我毕业后的第一个秋天，申请了域名，搭建了论坛。可惜好景不长，没多久进入论坛后就出现各种乱七八糟的广告，而这些广告压根都不是我加的。

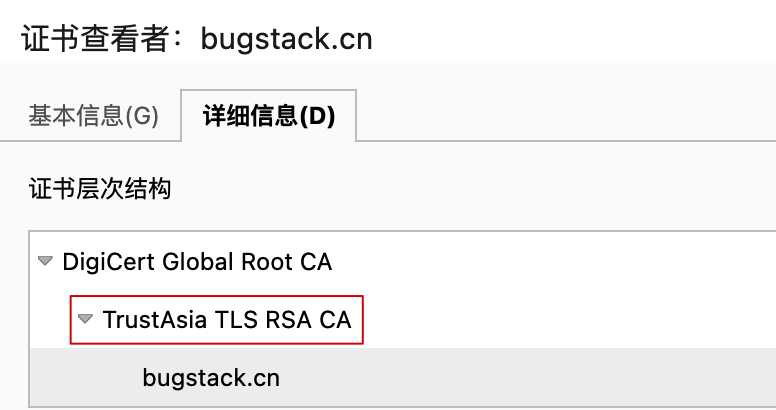
这是怎么回事？后来我才知道，原来我的论坛没有加 HTTPS 也就是没有 SSL 证书。那这和数学中的素数有啥关系呢？这是因为每一个 SSL 的生成都用到了 RSA 非对称加密，而 RSA 的加解密就是使用了两个互为质数的大素数生成公钥和私钥的。

这就是我们今天要分享的，关于素数在 RSA 算法中的应用。

一、什么是素数

素数（或质数）指的是大于1的且不能通过两个较小的自然数乘积得来的自然数。而大于1的自然数如果不是素数，则称之为合数。例如：7是素数，因为它的乘积只能写成 1 * 7 或者 7 * 1 这样。而像自然数 8 可以写成 2 * 4，因为它是两个较小数字的乘积。

通常在 Java 程序中，我们可以使用下面的代码判断一个数字是否为素数；

boolean isPrime = number > 0;

// 计算number的平方根为k，可以减少一半的计算量

int k = (int) Math.sqrt(number);

for (int i = 2; i <= k; i++) {

    if (number % i == 0) {

        isPrime = false;

        break;

    }

}

return isPrime;

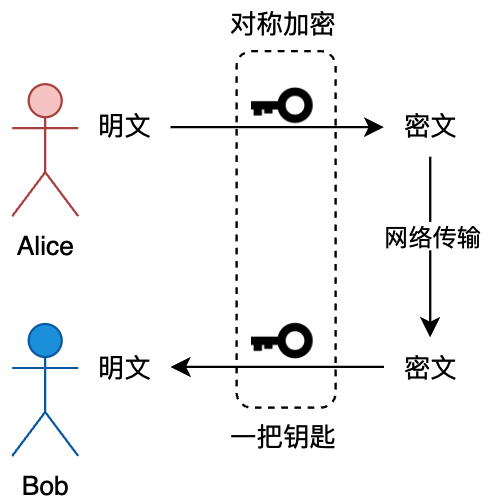
二、对称加密和非对称加密

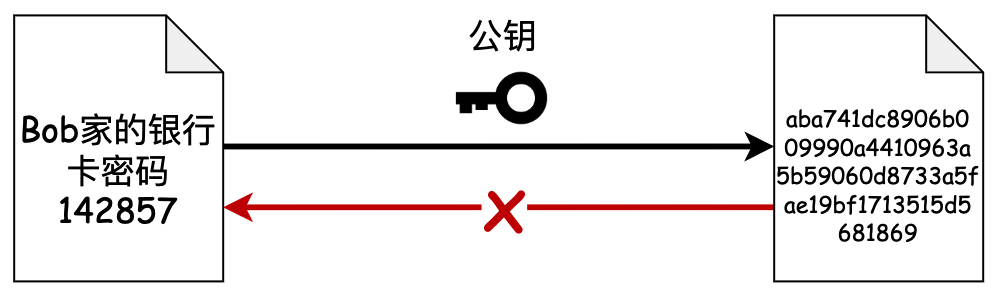
假如 Alice 时而需要给北漂搬砖的 Bob 发一些信息，为了安全起见两个人相互协商了一个加密的方式。比如 Alice 发送了一个银行卡密码 142857 给 Bob，Alice 会按照与 Bob 的协商方式，把 142857 * 2 = 285714 的结果传递给 Bob，之后 Bob 再通过把信息除以2拿到结果。

但一来二去，Alice 发的密码、生日、衣服尺寸、鞋子大小，都是乘以2的规律被别人发现。这下这个加密方式就不安全了。而如果每次都给不同的信息维护不同的秘钥又十分麻烦，且这样的秘钥为了安全也得线下沟通，人力成本又非常高。

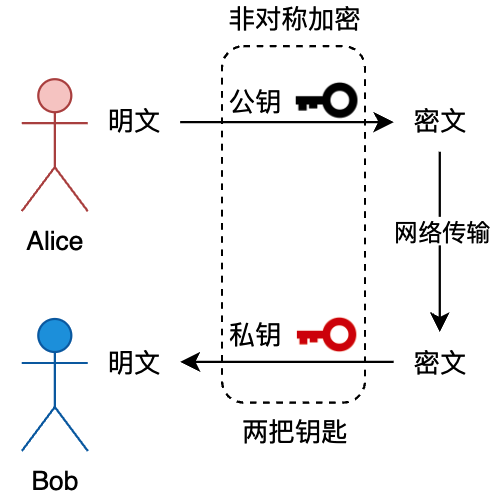
所以有没有另外一种方式，使用不同的秘钥对信息的加密和解密。当 Bob 想从 Alice 那获取信息，那么 Bob 就给 Alice 一个公钥，让她使用公钥对信息进行加密，而加密后的信息只有 Bob 手里有私钥才能解开。那么这样的信息传递就变得非常安全了。如图所示。

对称加密	非对称加密

三、算法公式推导

如果 Alice 希望更安全的给 Bob 发送的信息，那么就需要保证经过公钥加密的信息不那么容易被反推出来。所以这里的信息加密，会需用到求模运算。像计算机中的散列算法，伪随机数都是求模运算的典型应用。

例如；5^3 mod 7 = 6 —— 5的3次幂模7余6

5相当于 Alice 要传递给 Bob 的信息
3相当于是秘钥
6相当于是加密后的信息

经过求模计算的结果6，很难被推到出秘钥信息，只能一个个去验证；

5^1 mod 7 = 5

5^2 mod 7 = 3

5^3 mod 7 = 6

5^4 mod 7 = 2

...

但如果求模的值特别大，例如这样：5^3 mod 78913949018093809389018903794894898493... = 6 那么再想一个个计算就有不靠谱了。所以这也是为什么会使用模运算进行加密，因为对于大数来说对模运算求逆根本没法搞。

根据求模的计算方式，我们得到加密和解密公式；—— 关于加密和解密的公式推到，后文中会给出数学计算公式。

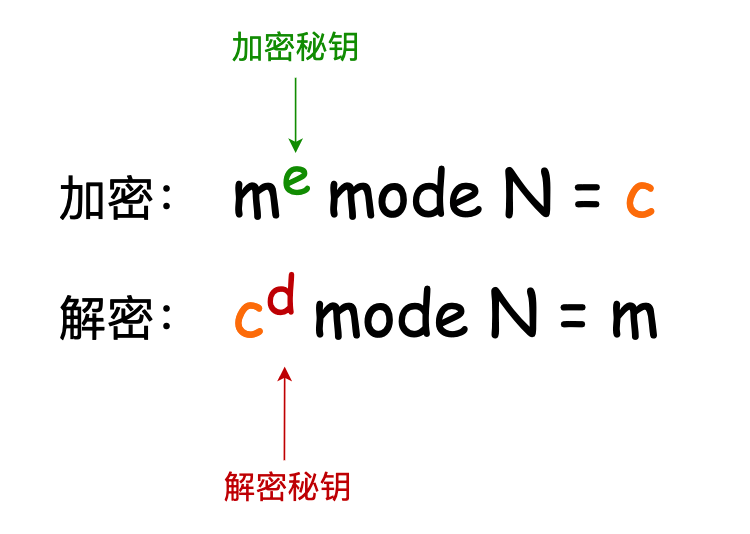
对于两个公式我们做一下更简单的转换；

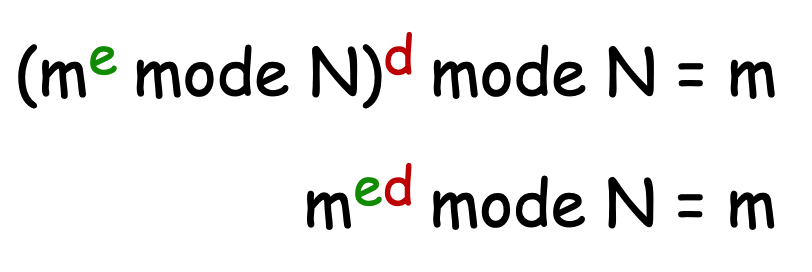
从转换后的公式可以得知，m 的 ed 次幂，除以 N 求求模可以得到 m 本身。那么 ed 就成了计算公钥加密的重要因素。为此这里需要提到数学中一个非常重要的定理，欧拉定理。—— 1763年，欧拉发现。

欧拉定理：m^φ(n) ≡ 1 (mod n) 对于任何一个与 n 互质的正整数 m，的 φ(n) 次幂并除以 n 去模，结果永远等于1。φ(n) 代表着在小于等于 n 的正整数中，有多少个与 n 互质的数。

例如：φ(8) 小于等于8的正整数中 1、2、3、4、5、6、7、8 有 1、3、5、7 与数字 8 互为质数。所以 φ(8) = 4 但如果是 n 是质数，那么 φ(n) = n - 1 比如 φ(7) 与7互为质数有1、2、3、4、5、6 所有 φ(7) = 6

接下来我们对欧拉公式做一些简单的变换，用于看出ed的作用；

经过推导的结果可以看到 ed = kφ(n) + 1，这样只要算出加密秘钥 e 就可以得到一个对应的解密秘钥 d。那么整套这套计算过程，就是 RSA 算法。

四、关于RSA算法

RSA加密算法是一种非对称加密算法，在公开秘钥加密和电子商业中被广泛使用。

于1977年，三位数学家；罗纳德·李维斯特（Ron Rivest）、阿迪·萨莫尔（Adi Shamir）和伦纳德·阿德曼（Leonard Adleman）设计了一种算法，可以实现非对称加密。这种算法用他们三个人的名字命名，叫做RSA算法。

1973年，在英国政府通讯总部工作的数学家克利福德·柯克斯（Clifford Cocks）在一个内部文件中提出了一个与之等效的算法，但该算法被列入机密，直到1997年才得到公开。

RSA 的算法核心在于取了2个素数做乘积求和、欧拉计算等一系列方式算得公钥和私钥，但想通过公钥和加密信息，反推出来私钥就会非常复杂，因为这是相当于对极大整数的因数分解。所以秘钥越长做因数分解越困难，这也就决定了 RSA 算法的可靠性。—— PS：可能以上这段话还不是很好理解，程序员‍还是要看代码才能悟。接下来我们就来编写一下 RSA 加密代码。

五、实现RSA算法

RSA 的秘钥生成首先需要两个质数p、q，之后根据这两个质数算出公钥和私钥，在根据公钥来对要传递的信息进行加密。接下来我们就要代码实现一下 RSA 算法，读者也可以根据代码的调试去反向理解 RSA 的算法过程，一般这样的学习方式更有抓手的感觉。嘿嘿抓手

1. 互为质数的p、q

两个互为质数p、q是选择出来的，越大越安全。因为大整数的质因数分解是非常困难的，直到2020年为止，世界上还没有任何可靠的攻击RSA算法的方式。只要其钥匙的长度足够长，用RSA加密的信息实际上是不能被破解的。—— 不知道量子计算机出来以后会不会改变。如果改变，那么程序员又有的忙了。

2. 乘积n

n = p * q 的乘积。

public long n(long p, long q) {

    return p * q;

}

3. 欧拉公式 φ(n)

φ(n) = (p - 1) * (q - 1)

public long euler(long p, long q) {

    return (p - 1) * (q - 1);

}

4. 选取公钥e

e 的值范围在 1 < e < φ(n)

public long e(long euler){

    long e = euler / 10;

    while (gcd(e, euler) != 1){

        e ++;

    }

    return e;

}

5. 选取私钥d

d = (kφ(n) + 1) / e

public long inverse(long e, long euler) {

    return (euler + 1) / e;

}

6. 加密

c = m^e mod n

public long encrypt(long m, long e, long n) {

    BigInteger bM = new BigInteger(String.valueOf(m));

    BigInteger bE = new BigInteger(String.valueOf(e));

    BigInteger bN = new BigInteger(String.valueOf(n));

    return Long.parseLong(bM.modPow(bE, bN).toString());

}

7. 解密

m = c^d mod n

public long decrypt(long c, long d, long n) {

    BigInteger bC = new BigInteger(String.valueOf(c));

    BigInteger bD = new BigInteger(String.valueOf(d));

    BigInteger bN = new BigInteger(String.valueOf(n));

    return Long.parseLong(bC.modPow(bD, bN).toString());

}

8. 测试

@Test

public void test_rsa() {

    RSA rsa = new RSA();

    long p = 3,                         // 选取2个互为质数的p、q

            q = 11,                     // 选取2个互为质数的p、q

            n = rsa.n(p, q),            // n = p * q

            euler = rsa.euler(p, q),    // euler = (p-1)*(q-1)

            e = rsa.e(euler),           // 互为素数的小整数e | 1 < e < euler

            d = rsa.inverse(e, euler),  // ed = φ(n) + 1 | d = (φ(n) + 1)/e

            msg = 5;                    // 传递消息 5

    System.out.println("消息：" + msg);

    System.out.println("公钥(n,e)：" + "(" + n + "," + e + ")");

    System.out.println("私钥(n,d)：" + "(" + n + "," + d + ")");

    long encrypt = rsa.encrypt(msg, e, n);

    System.out.println("加密（消息）：" + encrypt);

    long decrypt = rsa.decrypt(encrypt, d, n);

    System.out.println("解密（消息）：" + decrypt);

}

测试结果

消息：5

公钥(n,e)：(33,3)

私钥(n,d)：(33,7)

加密（消息）：26

解密（消息）：5

通过选取3、11作为两个互质数，计算出公钥和私钥，分别进行消息的加密和解密。如测试结果消息5的加密后的信息是26，解密后获得原始信息5

六、RSA数学原理

整个 RSA 的加解密是有一套数学基础可以推导验证的，这里小傅哥把学习整理的资料分享给读者，如果感兴趣可以尝试验证。这里的数学公式会涉及到；求模运算、最大公约数、贝祖定理、线性同于方程、中国余数定理、费马小定理。当然还有一些很基础的数论概念；素数、互质数等。以下推理数学内容来自博客：https://luyuhuang.tech/2019/10/24/mathematics-principle-of-rsa-algorithm.html

1. 模运算

1.1 整数除法

定理 1 令 a 为整数, d 为正整数, 则存在唯一的整数 q 和 r, 满足 0⩽r<d, 使得 a=dq+r.

当 r=0 时, 我们称 d 整除 a, 记作 d∣a; 否则称 d 不整除 a, 记作 d∤a

整除有以下基本性质:

定理 2 令 a, b, c 为整数, 其中 a≠0a≠0. 则:

对任意整数 m,n，如果 a∣b 且 a∣c, 则 a∣(mb + nc)
如果 a∣b, 则对于所有整数 c 都有 a∣bc
如果 a∣b 且 b∣c, 则 a∣c

1.2 模算术

在数论中我们特别关心一个整数被一个正整数除时的余数. 我们用 a mod m = b表示整数 a 除以正整数 m 的余数是 b. 为了表示两个整数被一个正整数除时的余数相同, 人们又提出了同余式(congruence).

定义 1 如果 a 和 b 是整数而 m 是正整数, 则当 m 整除 a - b 时称 a 模 m 同余 b. 记作 a ≡ b(mod m)

a ≡ b(mod m) 和 a mod m= b 很相似. 事实上, 如果 a mod m = b, 则 a≡b(mod m). 但他们本质上是两个不同的概念. a mod m = b 表达的是一个函数, 而 a≡b(mod m) 表达的是两个整数之间的关系.

模算术有下列性质:

定理 3 如果 m 是正整数, a, b 是整数, 则有

(a+b)mod m=((a mod m)+(b mod m)) mod m

ab mod m=(a mod m)(b mod m) mod m

根据定理3, 可得以下推论

推论 1 设 m 是正整数, a, b, c 是整数; 如果 a ≡ b(mod m), 则 ac ≡ bc(mod m)

证明 ∵ a ≡ b(mod m), ∴ (a−b) mod m=0 . 那么

(ac−bc) mod m=c(a−b) mod m=(c mod m⋅(a−b) mod m) mod m=0

∴ ac ≡ bc(mod m)

需要注意的是, 推论1反之不成立. 来看推论2:

推论 2 设 m 是正整数, a, b 是整数, c 是不能被 m 整除的整数; 如果 ac ≡ bc(mod m) , 则 a ≡ b(mod m)

证明 ∵ ac ≡ bc(mod m) , 所以有

(ac−bc)mod m=c(a−b)mod m=(c mod m⋅(a−b)mod m) mod m=0

∵ c mod m≠0 ,

∴ (a−b) mod m=0,

∴a ≡ b(mod m) .

2. 最大公约数

如果一个整数 d 能够整除另一个整数 a, 则称 d 是 a 的一个约数(divisor); 如果 d 既能整除 a 又能整除 b, 则称 d 是 a 和 b 的一个公约数(common divisor). 能整除两个整数的最大整数称为这两个整数的最大公约数(greatest common divisor).

定义 2 令 a 和 b 是不全为零的两个整数, 能使 d∣ad∣a 和 d∣bd∣b 的最大整数 d 称为 a 和 b 的最大公约数. 记作 gcd(a,b)

2.1 求最大公约数

如何求两个已知整数的最大公约数呢? 这里我们讨论一个高效的求最大公约数的算法, 称为辗转相除法. 因为这个算法是欧几里得发明的, 所以也称为欧几里得算法. 辗转相除法基于以下定理:

引理 1 令 a=bq+r, 其中 a, b, q 和 r 均为整数. 则有 gcd(a,b)=gcd(b,r)

证明我们假设 d 是 a 和 b 的公约数, 即 d∣a且 d∣b, 那么根据定理2, d 也能整除 a−bq=r 所以 a 和 b 的任何公约数也是 b 和 r 的公约数;

类似地, 假设 d 是 b 和 r 的公约数, 即 d∣bd∣b 且 d∣rd∣r, 那么根据定理2, d 也能整除 a=bq+r. 所以 b 和 r 的任何公约数也是 a 和 b 的公约数;

因此, a 与 b 和 b 与 r 拥有相同的公约数. 所以 gcd(a,b)=gcd(b,r).

辗转相除法就是利用引理1, 把大数转换成小数. 例如, 求 gcd(287,91) 我们就把用较大的数除以较小的数. 首先用 287 除以 91, 得

287=91⋅3+14

我们有 gcd(287,91)=gcd(91,14) . 问题转换成求 gcd(91,14). 同样地, 用 91 除以 14, 得

91=14⋅6+7

有 gcd(91,14)=gcd(14,7) . 继续用 14 除以 7, 得

14=7⋅2+0

因为 7 整除 14, 所以 gcd(14,7)=7. 所以 gcd(287,91)=gcd(91,14)=gcd(14,7)=7.

我们可以很快写出辗转相除法的代码:

def gcd(a, b):

    if b == 0: return a

    return gcd(b, a % b)

2.2 贝祖定理

现在我们讨论最大公约数的一个重要性质:

定理 4 贝祖定理 如果整数 a, b 不全为零, 则 gcd(a,b)是 a 和 b 的线性组合集 {ax+by∣x,y∈Z}中最小的元素. 这里的 x 和 y 被称为贝祖系数

证明令 A={ax+by∣x,y∈Z}. 设存在 x0x0, y0y0 使 d0d0 是 A 中的最小正元素, d0=ax0+by0 现在用 d0去除 a, 这就得到唯一的整数 q(商) 和 r(余数) 满足

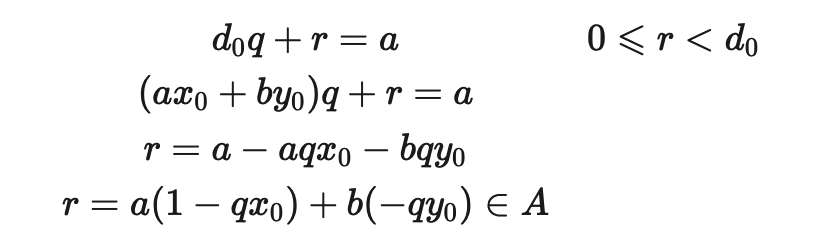
又 0⩽r<d0, d0 是 A 中最小正元素

∴ r=0 , d0∣a.

同理, 用 d0d0 去除 b, 可得 d0∣b. 所以说 d0 是 a 和 b 的公约数.

设 a 和 b 的最大公约数是 d, 那么 d∣(ax0+by0)即 d∣d0

∴∴ d0 是 a 和 b 的最大公约数.

我们可以对辗转相除法稍作修改, 让它在计算出最大公约数的同时计算出贝祖系数.

def gcd(a, b):

    if b == 0: return a, 1, 0

    d, x, y = gcd(b, a % b)

    return d, y, x - (a / b) * y

3. 线性同余方程

现在我们来讨论求解形如 ax≡b(modm) 的线性同余方程. 求解这样的线性同余方程是数论研究及其应用中的一项基本任务. 如何求解这样的方程呢? 我们要介绍的一个方法是通过求使得方程 ¯aa≡1(mod m) 成立的整数 ¯a. 我们称 ¯a 为 a 模 m 的逆. 下面的定理指出, 当 a 和 m 互素时, a 模 m 的逆必然存在.

定理 5 如果 a 和 m 为互素的整数且 m>1, 则 a 模 m 的逆存在, 并且是唯一的.

证明由贝祖定理可知, ∵ gcd(a,m)=1 , ∴ 存在整数 x 和 y 使得 ax+my=1 这蕴含着 ax+my≡1(modm) ∵ my≡0(modm), 所以有 ax≡1(modm)

∴ x 为 a 模 m 的逆.

这样我们就可以调用辗转相除法 gcd(a, m) 求得 a 模 m 的逆.

a 模 m 的逆也被称为 a 在模m乘法群 Z∗m 中的逆元. 这里我并不想引入群论, 有兴趣的同学可参阅算法导论

求得了 a 模 m 的逆 ¯a 现在我们可以来解线性同余方程了. 具体的做法是这样的: 对于方程 ax≡b(modm)a , 我们在方程两边同时乘上 ¯a, 得 ¯aax≡¯ab(modm)

把 ¯aa≡1(modm) 带入上式, 得 x≡¯ab(modm)

x≡¯ab(modm) 就是方程的解. 注意同余方程会有无数个整数解, 所以我们用同余式来表示同余方程的解.

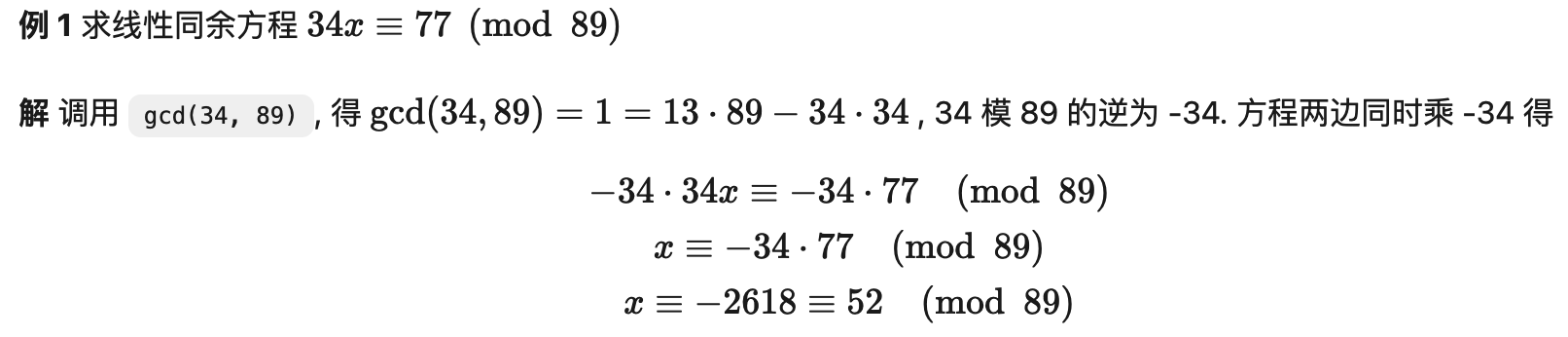
4. 中国余数定理

中国南北朝时期数学著作孙子算经中提出了这样一个问题:

有物不知其数，三三数之剩二，五五数之剩三，七七数之剩二。问物几何？

用现代的数学语言表述就是: 下列同余方程组的解释多少?

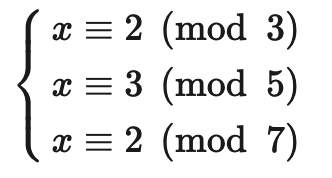
孙子算经 中首次提到了同余方程组问题及其具体解法. 因此中国剩余定理称为孙子定理.

定理 6 中国余数定理 令 m1,m2,…,mn 为大于 1 且两两互素的正整数, a1,a2,…,an 是任意整数. 则同余方程组

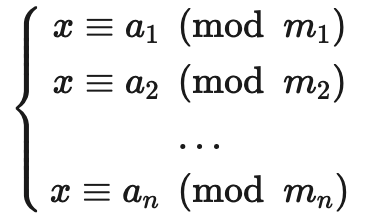
有唯一的模 m=m1m2…mnm=m1m2…mn 的解.

证明我们使用构造证明法, 构造出这个方程组的解. 首先对于 i=1,2,…,ni=1,2,…,n, 令

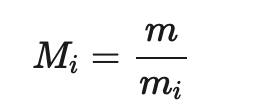
即, MiMi 是除了 mimi 之外所有模数的积. ∵∵ m1,m2,…,mn 两两互素, ∴∴ gcd(mi,Mi)=1. 由定理 5 可知, 存在整数 yiyi 是 MiMi 模 mimi 的逆. 即

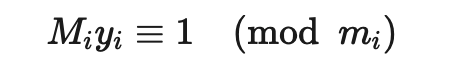
上式等号两边同时乘 aiai 得

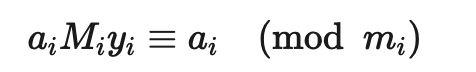
就是第 i 个方程的一个解; 那么怎么构造出方程组的解呢? 我们注意到, 根据 Mi 的定义可得, 对所有的 j≠ij≠i, 都有 aiMiyi≡0(modmj). 因此我们令

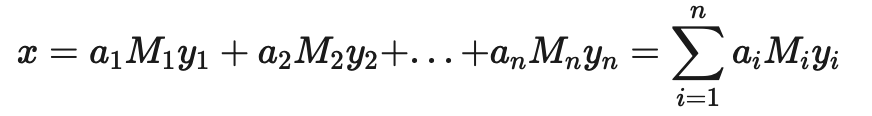
就是方程组的解.

有了这个结论, 我们可以解答 孙子算经 中的问题了: 对方程组的每个方程, 求出 MiMi , 然后调用 gcd(M_i, m_i) 求出 yiyi:

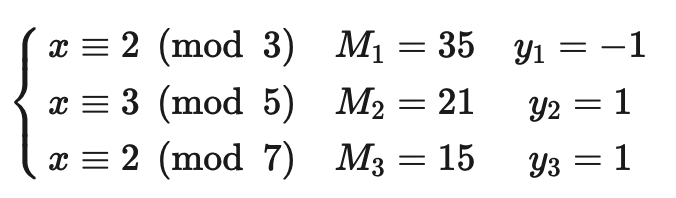
最后求出 x=−2⋅35+3⋅21+2⋅15=23≡23(mod105)

5. 费马小定理

现在我们来看数论中另外一个重要的定理, 费马小定理(Fermat's little theorem)

定理 7 费马小定理 如果 a 是一个整数, p 是一个素数, 那么

当 n 不为 p 或 0 时, 由于分子有质数p, 但分母不含p; 故分子的p能保留, 不被约分而除去. 即 p∣(np).

令 b 为任意整数, 根据二项式定理, 我们有

令 a=b+1, 即得 a^p ≡ a(mod p)

当 p 不整除 a 时, 根据推论 2, 有 a^p−1 ≡ 1(mod p)

6. 算法证明

我们终于可以来看 RSA 算法了. 先来看 RSA 算法是怎么运作的:

RSA 算法按照以下过程创建公钥和私钥:

随机选取两个大素数 p 和 q, p≠qp≠q;
计算 n=pq
选取一个与 (p−1)(q−1) 互素的小整数 e;
求 e 模 (p−1)(q−1) 的逆, 记作 d;
将 P=(e,n)公开, 是为公钥;
将 S=(d,n)保密, 是为私钥.

所以 RSA 加密算法是有效的.

(1) 式表明, 不仅可以用公钥加密, 私钥解密, 还可以用私钥加密, 公钥解密. 即加密计算 C=M^d mod n, 解密计算 M=C^e mod n

RSA 算法的安全性基于大整数的质因数分解的困难性. 由于目前没有能在多项式时间内对整数作质因数分解的算法, 因此无法在可行的时间内把 n 分解成 p 和 q 的乘积. 因此就无法求得 e 模 (p−1)(q−1)的逆, 也就无法根据公钥计算出私钥.

七、常见面试题

质数的用途
RSA 算法描述
RSA 算法加解密的过程
RSA 算法使用场景
你了解多少关于 RSA 的数学数论知识

RSA加密算法：https://zh.wikipedia.org/wiki/RSA%E5%8A%A0%E5%AF%86%E6%BC%94%E7%AE%97%E6%B3%95
RSA算法原理： https://www.ruanyifeng.com/blog/2013/07/rsa_algorithm_part_two.html
RSA算法背后的数学原理：https://luyuhuang.tech/2019/10/24/mathematics-principle-of-rsa-algorithm.html
莱昂哈德·欧拉：https://en.wikipedia.org/wiki/Leonhard_Euler