理解HMM算法

长这样：

理解的前提：

　　（1）状态：生成观测值的变量（上图中的“吃”和“睡”）。

　　（2）观测值：状态乘上输出概率对应的输出（上图中的橙色节点）。

　　（3）输出概率：输出概率矩阵里面的某个元素（状态和观测值两层之间的某个权重参数）。

　　（4）输出概率矩阵：由输出概率组成的矩阵。

　　（5）b_i: 第i个状态（比如”睡“）输出所有观测值对应的概率构成的行向量（上图中所有红线构成的行向量）。

　　（6）o₁：表示我要输出第一个观测值。不是把o₁做为自变量输入到b_i中，只是一个记号（个人表示没什么用）。

　　（7）Π_i：走 第i个状态的初始概率（p(start->吃)=0.3)。

　　（8）α_i(t)：（阿尔法）在给定马尔可夫模型中，到t时刻为止，状态们在t个时刻，每个时刻都由所有状态中的一个输出某个观测值，一共输出了t个观测值观测序列，记为,，并且t时刻输出O_t的状态为q_i（状态用q表示），把出现上述场景的概率记作α_i(t)，称作前向概率（应该是在做前向计算，所以形象成为”前向概率“）。

　　　　　

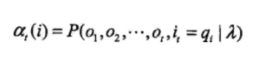
（9）a_ij：（字母a，注意不是阿尔法，在第一张图中的“推导”公式里面的）概率转移矩阵中第i行，第j列对应的概率（今天为第i个状态，明天为第j个状态的概率。网络图示中“吃->吃”、“吃->睡”和“睡->睡”之间连线的数　　　　　　　　值）。

　　（10）转移概率矩阵：如下图A所示。

理解

：

表示第1时刻，第i个状态的初始概率Π_i乘以第i个状态对应的输出矩阵的第i行向量。

例如：假设第i个状态为“睡”，那么Π_i等于0.7，b_i等于[0.3,0.5,0.2]，那么第1时刻的状态为“睡”，观测值为“哭”、“没精神”和“找妈妈”的概率分别为0.7*[0.3,0.5,0.2]，如果第一时刻的观测值为“哭”，那么α₁(t)=0.21.

：

t+1时刻，所有t时刻的前向概率里面按时的t时刻的状态转化为j状态后再乘以j对应的输出概率总和。

以第2时刻为例：状态j为“吃”，那么α_j(t+1)表示第二时刻，第二状态为“吃”，观测值序列为的O₁O₂概率，其等于第1时刻的前向概率α_i(t) 乘以 第一时刻的前向概率里面暗示的第一时刻的状态i转化为状态j的概率(a_ij),i有可能是“吃”，也有可能是“睡”，我们要计算的是第2时刻状态为“吃”的概率，根据马尔可夫模型，第二时刻的“吃”和第一时刻的状态有关，但是我们不知道第一时刻到底是什么状态，所以用概率的方式全部考虑进来。

[0.21,0.03,0.02]*0.1*b_jo2(0.1表示“吃₁”->“吃₂”的概率）+[0.21,0.15,0.14]*0.9*b_jo2(0.9表示“睡₁”->“吃₂”的概率）

乘上转移概率之后，在乘以“吃”对应的输出概率行向量：

[0.021,0.003,0.002]^Tx[0.7,0.1,0.2] + [0.189,0.135,0.126]^Tx[0.7,0.1,0.2]（考虑了所有情况，可能会有点费解，请看下一行）

如果第一时刻的观测值为“哭”，第二时刻的状态为“吃”,观测值为“哭”，那么α_j(t+1)=0.21*0.1*0.7=0.0147 + 0.21*.0.9*0.7=0.1323.

：

μ：给定的马尔可夫模型。

O：1-T+1时刻的观测值序列。

在马尔可夫模型μ中，输出序列O的概率为：输出O并且T+1时刻的状态为q_i的概率综合。

本文截图部分来自：隐马尔科夫模型（HMM）一前向与后向算法 - 知乎 (zhihu.com)