Codeforces Round #133 (Div. 2), A.【据图推公式】 B.【思维+简单dfs】

Problem - 216A - Codeforces

Problem - B - Codeforces

A Tiling with Hexagons

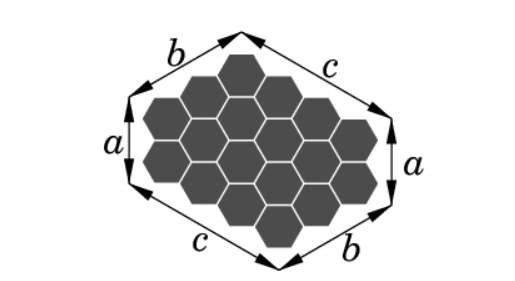
题意： 给出a b c ，求里面有多少个六边形

题解：将六边形补全为平行四边形，如图b  c延长，把a覆盖，直接底*高 - 2* 补全的小三角形

#include <iostream>

using namespace std;

int main()
{
    int a, b, c;
    cin >> a >> b >> c;
    cout << (b+a-1)*(c+a-1)-a*(a-1)<<endl;
    return 0;
}

B  Forming Teams

题意：n个人，组成两个队，不能让敌人在一起。共n个人，m对敌人，每个人最多两个敌人。我们可以去一些人使两队人数相等且没有敌人在一起，求最少去多少人。

题解：有三种情况1.单边 2.双数环  3.单数环    对于1和2是可以平均分到两队的，而3就需要去掉一个人，还有就是最后的人数要是双数。

#include <iostream>

using namespace std;

int n, res = 0;
int a[110][110];
void dfs(int init, int x, int num)
{
    int flag = 0;
    for(int i = 1; i <= n; i ++)
    {
        if(a[x][i] == 1)
        {
            a[x][i] = 0;
            a[i][x] = 0;
            if(i == init)
            {
                flag = 2;
                num ++;
                break;
            }
            dfs(init, i, num+1);
        }
    }
    if(flag==2 && num > 2 && num%2==1)
        res ++;
}

int main()
{
    int m;
    cin >> n >> m;
    while(m --)
    {
        int x, y;
        cin >> x >> y;
        a[x][y] = 1;
        a[y][x] = 1;
    }

    for(int i = 1; i <= n; i ++)
    {
        dfs(i, i, 0);
    }
    if((n-res)%2)res++;
    cout << res <<endl;
    return 0;
}