[HNOI2010]弹飞绵羊 （平衡树，LCT动态树）

题面

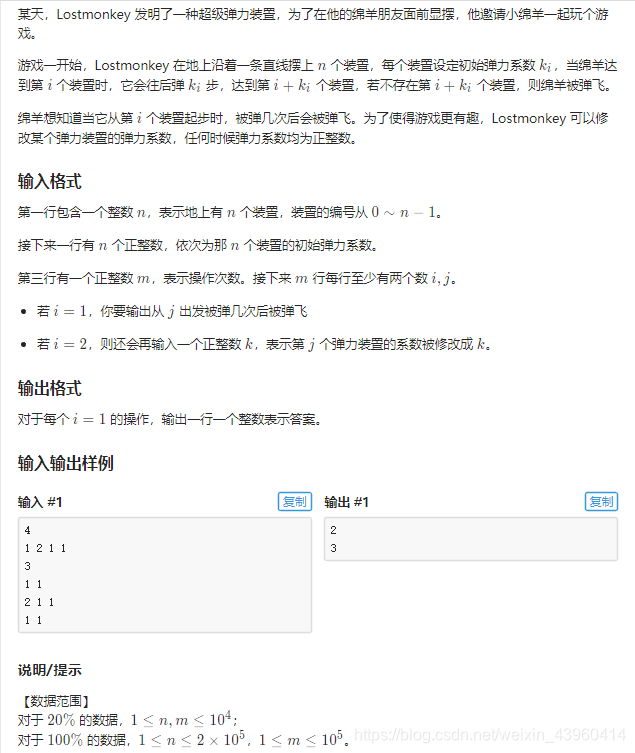
题解

因为每个点都只能向后跳到一个唯一的点，但可能不止一个点能跳到后面的某个相同的点，

所以我们把它抽象成一个森林。（思考：为什么是森林而不是树？）

子节点可以跳到父节点，根节点再跳就跳飞了。

由于我们发现有一些父子关系要变，所以不能用树链剖分等静态的数据结构，可以用LCT（Link-Cut-Tree 联-切-树，即动态树，支持动态修改父子关系）。

但是当我们询问答案的时候，我们发现wa了，那是因为我们询问的是x点到根的路径上的点数，但是各种LCT操作已经把原先的根不知换到那里去了，所以整个过程中，我们要维护树的根不变。

这个其实很简单，每次进行涉及换根操作时，我们都把原先的根存一下（Findroot()/Find()），操作完后，再把根换回去（Makeroot()），全过程中，当发现x + kx大于n时，就Makeroot(x)。

（由于是道数据结构题，题解写得真的不是很长，请尽量理解吧）

ＣＯＤＥ

LCT建议压行，不仅好改而且好看。

#include<cstdio>
#include<iostream>
#include<cstring>
#include<vector>
#include<queue>
#include<stack>
#include<cmath>
#include<algorithm>
#include<map>
#include<stack>
#define LL long long
#define MAXN 2000050
#define DB double
#define lowbit(x) ((-x & x))
#define rg register
using namespace std;
inline LL read() {
	LL f = 1,x = 0;char s = getchar();
	while(s < '0' || s > '9') {if(s == '-') f = -1;s = getchar();}
	while(s >= '0' && s <= '9') {x = x * 10 + s - '0';s = getchar();}
	return x * f;
}
int n;
int m,i,j,s,o,k;
//--------------------------key numbers-------------------------------
struct tr{
	int s[2],fa;
	int siz;
	int nm,as;
	int lzn,lzr;// lzn其实不需要，只是懒得删
	tr(){s[0] = s[1] = 0;nm = 0;siz = 0;lzn = lzr = 0;as = 0;}
}tre[MAXN];int cnt_splay = 0,st[MAXN],sttop = 0;
inline int newnode(int nm) {
	int ct = ++cnt_splay;
	tre[ct] = tr();
	tre[ct].nm = nm;
	tre[ct].as = nm;
	tre[ct].siz = 1;
	return ct;
}
inline bool isroot(int x) {
	if(tre[tre[x].fa].s[1] == x || tre[tre[x].fa].s[0] == x) return 0;
	return 1;
}
inline void update(int x) {
	int l=tre[x].s[0],r = tre[x].s[1];tre[0] = tr();
	tre[x].as = tre[x].nm + tre[l].as + tre[r].as;
	tre[x].siz = tre[l].siz + tre[r].siz + 1;
	tre[l].fa = x;tre[r].fa = x;tre[0] = tr();
}
inline void changer(int x) {swap(tre[x].s[0],tre[x].s[1]); tre[x].lzr ^= 1;}
inline void pushdown(int x) {
	if(!x) return ;
	if(tre[x].lzr) {
		changer(tre[x].s[0]);
		changer(tre[x].s[1]);
		tre[x].lzr = 0;
	}return ;
}
inline void pushup(int x) {
	sttop = 0;st[++sttop] = x;
	for(int f = x;!isroot(f); f = tre[f].fa) st[++sttop] = tre[f].fa;
	while(sttop) pushdown(st[sttop --]);
}
inline void rotate(int x) {
	int y = tre[x].fa,z = tre[y].fa;
	int d = (tre[y].s[1] == x);
	if(!isroot(y)) tre[z].s[tre[z].s[1] == y] = x;
	tre[x].fa = z;
	tre[y].s[d] = tre[x].s[d^1];
	if(tre[y].s[d]) tre[tre[y].s[d]].fa = y;
	tre[x].s[d^1] = y;
	tre[y].fa = x;
	update(y);update(x);
}
inline void splay(int x) {
	pushup(x);
	while(!isroot(x)) {
		int y = tre[x].fa,z = tre[y].fa;
		if(!isroot(y)) {
			if((tre[y].s[1] == x) ^ (tre[z].s[1] == y)) rotate(x);
			else rotate(y);
		}
		rotate(x);
	}
	update(x); return ;
}
inline void wash() {splay(rand() % cnt_splay + 1);}
//--------------------------splay-------------------------------------
inline void Access(int x) {
	for(int pre = 0; x; pre = x,x = tre[x].fa) {
		splay(x);
		tre[x].s[1] = pre;
		update(x);
	}return ;
}
inline void Maketop(int x) {Access(x);splay(x);}
inline void Makeroot(int x) {Access(x); splay(x); changer(x);}
inline int  Findroot(int x) {for(Maketop(x); tre[x].s[0]; x = tre[x].s[0]); splay(x); return x;}
inline void Change(int x,int nm) {Maketop(x); tre[x].nm = nm; update(x);}
//##### no Makeroot() inside
inline void Link(int x,int y) {Makeroot(x); tre[x].fa = y;}
inline void Cut(int x,int y) {Makeroot(x); Maketop(y); tre[y].s[0] = tre[x].fa = 0; update(y); pushup(x);}
inline int  Getline(int x,int y) {Makeroot(x); Maketop(y); update(y); return y;}
inline bool Haveedge(int x,int y) {Makeroot(x); Maketop(y); return tre[x].fa == y;}
//-------------------------Link Cut Tree------------------------------
char ss[20];
int ki[MAXN];
int main() {
	n = read();
	cnt_splay = 0;
	for(int i = 1;i <= n+3;i ++) {
		newnode(1);
	}
	for(int i = 1;i <= n;i ++) {
		ki[i] = read();
		if(i + ki[i] <= n) Link(i,i + ki[i]);
		else Makeroot(i);
	}
	m = read();
	while(m --) {
		k = read();
		if(k == 1) {
			s = read() + 1;
			Access(s);
			splay(s);
			printf("%d\n",tre[s].as);
		}
		else if(k == 2) {
			s = read() + 1;o = read();
			if(s + ki[s] <= n) {
				int v = s + ki[s];
				int rt = Findroot(v);
				Cut(s,v);
				Makeroot(rt);
			}
			ki[s] = o;
			if(s + ki[s] > n) Makeroot(s);
			else {
				int rt = Findroot(s + ki[s]);
				Link(s,s + ki[s]);
				Makeroot(rt);
			}
		}
	}
	return 0;
}