SDOI Day2

今天做了SDOI Day2 觉得自己萌萌哒= =题目真的有点水，一点编程复杂度都没有

T1：星际战争

描述：http://www.lydsy.com/JudgeOnline/problem.php?id=3993

这道题是这两天最容易的题了吧。。

可以发现这是一个二分图，考虑二分答案，那么人们在这段时间的输出伤害就能够确定了，用最大流判断是否所有的机器人护甲值都为0，即可。

数据较良心跑得飞快

Code：

 #include<cstdio>
 #include<iostream>
 #include<cstring>
 #include<algorithm>
 using namespace std;
 #define maxn 105
 #define maxm 3000
 struct edges{
     int to,next;double cap;
 }edge[maxm*];
 int l,next[maxn];
 inline void addedge(int x,int y,double z) {
     l++;
     edge[l*]=(edges){y,next[x],z};next[x]=l*;
     edge[l*+]=(edges){x,next[y],};next[y]=l*+;
 }
 int p[maxn],gap[maxn],h[maxn],s,t;
 double sap(int u,double flow) {
     if (u==t) return flow;
     double cnt=;
     for (int i=p[u];i;i=edge[i].next)
         if (edge[i].cap&&h[edge[i].to]+==h[u]) {
             double cur=sap(edge[i].to,min(flow-cnt,edge[i].cap)) ;
             edge[i].cap-=cur;edge[i^].cap+=cur;
             p[u]=i;
             if ((cnt+=cur)==flow) return flow;
         }
     if (!(--gap[h[u]])) h[s]=t;
     gap[++h[u]]++;
     p[u]=next[u];
     return cnt;
 }
 inline double maxflow(){
     for (int i=;i<=t;i++) p[i]=next[i];
     memset(h,,sizeof(h));
     memset(gap,,sizeof(gap));
     gap[]=t;
     double flow=;
     while (h[s]<t) flow+=sap(s,1e7);
     return flow;
 }
 int a[maxn],b[maxn];
 bool c[maxn][maxn];
 int n,m;
 inline void build(double mid){
     l=;
     s=n+m+,t=n+m+;
     memset(next,,sizeof(next));
     for (int i=;i<=n;i++) addedge(s,i,mid*a[i]);
     for (int i=;i<=m;i++) addedge(i+n,t,b[i]);
     for (int i=;i<=n;i++)
         for (int j=;j<=m;j++)
             if (c[i][j]) addedge(i,j+n,5e6);
 }
 int main(){
     scanf("%d%d",&m,&n);
     int sum=;
     for (int j=;j<=m;j++) {
         scanf("%d",b+j);sum+=b[j];
     }
     for (int i=;i<=n;i++) scanf("%d",a+i);
     for (int i=;i<=n;i++)
         for (int j=;j<=m;j++) scanf("%d",c[i]+j);
     double l=,r=5e6;
     while (r-l>1e-) {
         double mid=(l+r)/;
         build(mid);
         if (maxflow()<sum) l=mid;
         else r=mid;
     }
     printf("%lf\n",r);
     return ;
 }

T2:约数个数和

描述：http://www.lydsy.com/JudgeOnline/problem.php?id=3994

数论渣= =贴下别人的题解吧= =http://blog.codebursts.com/bzoj3994/

顺便说一下自己YY出来的另一种解法，记f[i][j][k]为n=i,m=j中n*m的最小质因数大于pri[k]的答案

那么f[i][j][k]=sigma(f[i/(x^a)][j/(x^b)][k+1]*(a+b+1))

好像很漂亮的样子，但是时间复杂度我不知道怎么样，求大神給我解答QAQ

T3：道路修建

描述：http://www.lydsy.com/JudgeOnline/problem.php?id=3995

看到这个下意识就想到线段树了= =

一共有3种解法

解法一：当合并区间时，连上两条边变成一个环套树，然后删去环上最大的边

我们考虑维护每个区间最左右的一个类似C型结构，可以发现只有当删去的边为纵边同时这个小区间只有一条纵边时大区间的这个东西才会改变，否则都是小区间的左右值。

保存左右两边C的横边最大值以及纵边最大值还有纵边数量即可

解法二：考虑直接生成新区间的树

可以发现这个区间只有可能是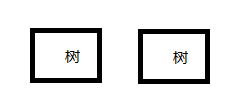或

那么怎么维护这个联通块—联通块的问题呢= =

有3种情况= =

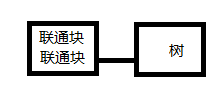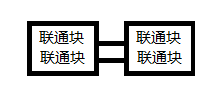或还有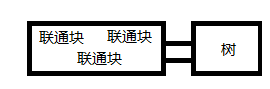

然后考虑怎么维护联通块—联通块—联通块的问题了= =

我去这怎么办啊

据某位同学透露，这个一共只有3种情况所以可以直接维护(我去我怎么搞出了超多种情况= =，但人家还真的a了而且跑得飞快= =)

具体的实现方法可以私信我

解法三：

可以看出，可能成为树的是该区间的所有点都和暴露在外面的四个点之一相连，所以我们可以考虑用联通性的方法来解决这道题

枚举所有的联通性并考虑转移，还是能写的= =

时间上就有点拙计了

Code:（解法一）

 #include<cstdio>
 #include<iostream>
 #include<cstring>
 #include<algorithm>
 using namespace std;
 #define maxn 60010
 struct bo{
     int c[],cost,mx[][];bool flag;
 };
 inline bo update(bo x,bo y){
     bo ans;
     ans.c[]=y.c[];
     ans.c[]=y.c[];
     ans.cost=x.cost+y.cost+x.c[]+x.c[];
     ans.mx[][]=x.mx[][],ans.mx[][]=x.mx[][];
     ans.mx[][]=y.mx[][],ans.mx[][]=y.mx[][];
     int tmp=max(max(x.mx[][],y.mx[][]),max(x.c[],x.c[]));
     if (tmp>=max(x.mx[][],y.mx[][])) {
         ans.cost-=tmp;ans.flag=;return ans;
     }
     ans.flag=x.flag&y.flag;
     if (x.mx[][]>y.mx[][]) {
         ans.cost-=x.mx[][];
         if (x.flag) {
             ans.mx[][]=max(ans.mx[][],tmp);
             ans.mx[][]=y.mx[][];
         }
         return ans;
     }
     ans.cost-=y.mx[][];
     if (y.flag) {
         ans.mx[][]=max(ans.mx[][],tmp);
         ans.mx[][]=x.mx[][];
     }
     return ans;
 }

 int a[maxn][];
 struct node{
     int l,r;bo b;
 }t[maxn*];
 #define mid ((l+r)>>1)
 #define lc (x<<1)
 #define rc (lc^1)
 void build(int x,int l,int r){
     t[x].l=l;t[x].r=r;
     if (l==r) {
         t[x].b.c[]=a[l][];
         t[x].b.c[]=a[l][];
         t[x].b.cost=a[l][];
         t[x].b.flag=;
         memset(t[x].b.mx,,sizeof(t[x].b.mx));
         t[x].b.mx[][]=t[x].b.mx[][]=a[l][];
         return ;
     }
     build(lc,l,mid);build(rc,mid+,r);
     t[x].b=update(t[lc].b,t[rc].b);
 }
 void set(int x,int y){
     int l=t[x].l,r=t[x].r;
     if (l>y||r<y) return ;
     if (l==r) {
         t[x].b.c[]=a[l][];
         t[x].b.c[]=a[l][];
         t[x].b.cost=a[l][];
         t[x].b.flag=;
         memset(t[x].b.mx,,sizeof(t[x].b.mx));
         t[x].b.mx[][]=t[x].b.mx[][]=a[l][];
         return ;
     }
     set(lc,y);set(rc,y);
     t[x].b=update(t[lc].b,t[rc].b);
 }
 bo query(int x,int x1,int y1) {
     int l=t[x].l,r=t[x].r;
     if (x1<=l&&r<=y1) return t[x].b;
     if (y1<=mid) return query(lc,x1,y1);
     if (mid<x1) return query(rc,x1,y1);
     return update(query(lc,x1,y1),query(rc,x1,y1));
 }
 int main(){
     int n,m;
     scanf("%d%d",&n,&m);
     for (int i=;i<n;i++) scanf("%d",&a[i][]);
     for (int i=;i<n;i++) scanf("%d",&a[i][]);
     for (int i=;i<=n;i++) scanf("%d",&a[i][]);
     build(,,n);
     while (m--) {
         char opt[];
         int x0,x1,y0,y1,z;
         bo x,y;
         scanf("%s",opt);
         switch (opt[]) {
             case 'Q' :
                 scanf("%d%d",&x1,&y1);
                 printf("%d\n",query(,x1,y1).cost);
                 break;
             case 'C':
                 scanf("%d%d%d%d%d",&x0,&y0,&x1,&y1,&z);
                 if (y0>y1) swap(y0,y1);
                 if (y0==y1) a[y0][]=z;
                 else a[y0][x0-]=z;
                 set(,y0);
                 break;
         }
     }
     return ;
 }