C4.5算法总结

C4.5是一系列用在机器学习和数据挖掘的分类问题中的算法。它的目标是监督学习：给定一个数据集，其中的每一个元组都能用一组属性值来描述，每一个元组属于一个互斥的类别中的某一类。C4.5的目标是通过学习，找到一个从属性值到类别的映射关系，并且这个映射能用于对新的类别未知的实体进行分类。

C4.5由J.Ross Quinlan在ID3的基础上提出的。ID3算法用来构造决策树。决策树是一种类似流程图的树结构，其中每个内部节点（非树叶节点）表示在一个属性上的测试，每个分枝代表一个测试输出，而每个树叶节点存放一个类标号。一旦建立好了决策树，对于一个未给定类标号的元组，跟踪一条有根节点到叶节点的路径，该叶节点就存放着该元组的预测。决策树的优势在于不需要任何领域知识或参数设置，适合于探测性的知识发现。

从ID3算法中衍生出了C4.5和CART两种算法，这两种算法在数据挖掘中都非常重要。下图就是一棵典型的C4.5算法对数据集产生的决策树。

比如我们判断一个人能不能结婚，那么每个人就可以作为一个具体的对象，该对象有着很多属性，比如年龄，性别，帅不帅，工作NB不，有没有女朋友，是不是富二代6个属性，而结婚也作为该对象的一个属性，而”结婚”属性就可以作为我们的预测属性！然后根据其他属性来预测我们的目标属性--结婚属性，比如说，年龄：30，性别：男，长的帅，工作不错，又女朋友，还是富二代！根据这些属性我们就可以得出该人今年可以结婚！当然这是预测出来的！这时，我们肯定有个疑问了，这是如何预测的呢？这实质上是根据我们的统计数据得出的，比如我们统计10000个人，根据这一万个人的6个属性以及目标属性（结婚）最终得出一组数据，我们用这组数据做成一个决策树！而其中这10000个人的样本我们则称为训练样本！

我们还是拿”打高尔夫球”这个经典的例子来作具体研究吧!该例其实就是通过一些列的属性来决定是否适合打高尔夫！刚刚说了训练样本，我们就来看看训练样本吧！图1是我用WPF做了一个简单的CRUD界面，用来把我们的样本显示的展现出来。具体看图1。。

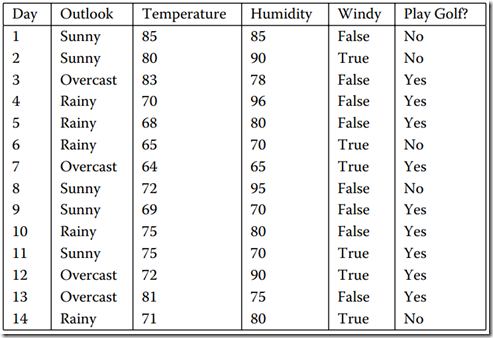
图1  数据集

我们从图中可以看出，该表中共有6列，而每一列中的列名对应一个属性，而我们以实践经验知道，“Day”即日期这个属性并不能帮我们预测今天是否适合去打Golf.故该属性我们就应该选择摒弃！再看该系统中的其他5给属性。很显然，图1中我用红笔画出来的属性“Play Golf”该属性就是我们的预测属性。而其他4个属性“Outlook”（天气）”、Temperature”（温度） 、“Humdity”（湿度）、“Windy”(是否刮风)这四个属性进行判断今天去 Play Golf。

那我们接下来的工作自然就是根据属性1-4得出我们的决策树了!那么我们来想想该决策树的算法，实质上其遵循一种统一的递归模式：即，首先用根节点表示一个给定的数据集（比如在这，就是我们的14个样本）；然后，从根节点开始在每个节点上测试一个特定的属性，把节点数据集划分成更小的子集（这一步，比如根据属性Outlook划分，可以划分出三个子集出来，即属于Sunny的一个子集样本，属于Overcast的子集样本，属于Rainy的子集样本），该子集并用子树进行表示；该过程就开始一直进行，直到子集称为“纯的”,也就是说直到子集中的所有实例都属于同一个类别，树才停止生长。

根据算法产生的决策树：

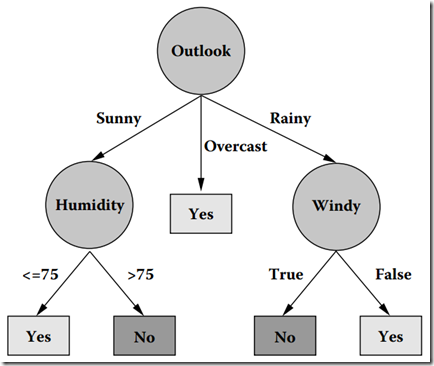
图2   在数据集上通过C4.5生成的决策树

看图2，首先是根据Outlook属性进行划分，根据Outlook的三个属性值（Sunny、Overcast、Rainy）划分出了三个组合，而其中Overcast划分中的集合是“纯”的了。故此子树就停止生长了。而根据Sunny属性值划分中的样例集合1，2，8，9，11显然还不是“纯”的（该组样例中有的PlayGolf是Yes,而有的是No）,故需要再次对其进行划分，直到分组中的所有样例都是“纯”的位置，才停止生长。

算法描述

C4.5并不一个算法，而是一组算法—C4.5，非剪枝C4.5和C4.5规则。下图中的算法将给出C4.5的基本工作流程：

图3  C4.5算法流程

我们可能有疑问，一个元组本身有很多属性，我们怎么知道首先要对哪个属性进行判断，接下来要对哪个属性进行判断？换句话说，在图2中，我们怎么知道第一个要测试的属性是Outlook，而不是Windy？其实，能回答这些问题的一个概念就是属性选择度量。

属性选择度量

属性选择度量又称分裂规则，因为它们决定给定节点上的元组如何分裂。属性选择度量提供了每个属性描述给定训练元组的秩评定，具有最好度量得分的属性被选作给定元组的分裂属性。目前比较流行的属性选择度量有--信息增益、增益率和Gini指标。

先做一些假设，设D是类标记元组训练集，类标号属性具有m个不同值，m个不同类Ci(i=1,2,…，m)，CiD是D中Ci类的元组的集合，|D|和|CiD|分别是D和CiD中的元组个数。

（1）信息增益

信息增益实际上是ID3算法中用来进行属性选择度量的。它选择具有最高信息增益的属性来作为节点N的分裂属性。该属性使结果划分中的元组分类所需信息量最小。对D中的元组分类所需的期望信息为下式：

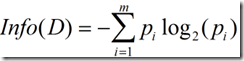 （1）

Info(D)又称为熵。

现在假定按照属性A划分D中的元组，且属性A将D划分成v个不同的类。在该划分之后，为了得到准确的分类还需要的信息由下面的式子度量：

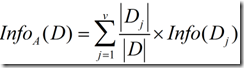       （2）

信息增益定义为原来的信息需求（即仅基于类比例）与新需求（即对A划分之后得到的）之间的差，即

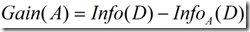       （3）

我想很多人看到这个地方都觉得不是很好理解，所以我自己的研究了文献中关于这一块的描述，也对比了上面的三个公式，下面说说我自己的理解。

一般说来，对于一个具有多个属性的元组，用一个属性就将它们完全分开几乎不可能，否则的话，决策树的深度就只能是2了。从这里可以看出，一旦我们选择一个属性A，假设将元组分成了两个部分A1和A2，由于A1和A2还可以用其它属性接着再分，所以又引出一个新的问题：接下来我们要选择哪个属性来分类？对D中元组分类所需的期望信息是Info(D) ,那么同理，当我们通过A将D划分成v个子集Dj(j=1,2,…,v)之后，我们要对Dj的元组进行分类，需要的期望信息就是Info(Dj),而一共有v个类，所以对v个集合再分类，需要的信息就是公式（2）了。由此可知，如果公式（2）越小，是不是意味着我们接下来对A分出来的几个集合再进行分类所需要的信息就越小？而对于给定的训练集，实际上Info(D)已经固定了，所以选择信息增益最大的属性作为分裂点。

但是，使用信息增益的话其实是有一个缺点，那就是它偏向于具有大量值的属性。什么意思呢？就是说在训练集中，某个属性所取的不同值的个数越多，那么越有可能拿它来作为分裂属性。例如一个训练集中有10个元组，对于某一个属相A，它分别取1-10这十个数，如果对A进行分裂将会分成10个类，那么对于每一个类Info(Dj)=0，从而式（2）为0，该属性划分所得到的信息增益（3）最大，但是很显然，这种划分没有意义。

（2）信息增益率

正是基于此，ID3后面的C4.5采用了信息增益率这样一个概念。信息增益率使用“分裂信息”值将信息增益规范化。分类信息类似于Info(D)，定义如下：

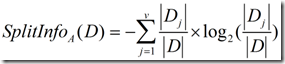    （4）

这个值表示通过将训练数据集D划分成对应于属性A测试的v个输出的v个划分产生的信息。信息增益率定义：

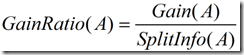         （5）

选择具有最大增益率的属性作为分裂属性。

（3）Gini指标

Gini指标在CART中使用。Gini指标度量数据划分或训练元组集D的不纯度，定义为：

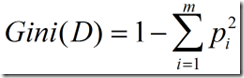         （6）

C#实现代码如下：

计算信息增益率：

 using System;
 using System.Collections;
 using System.Collections.Generic;
 using System.Data;
 using System.Linq;
 using System.Text;
 using System.Threading.Tasks;

 namespace C4._5.BLL
 {
     public class Entropy
     {
         public int[] statNum = new int[];//训练统计结果:0->No  1->Yes
         public double EntropyValue = ;
         private int mTotal = ;
         private string mTargetAttribute = "PlayGolf";

         public void getEntropy(DataTable samples)
         {
             CountTotalClass(samples,out statNum[],out statNum[]);
             EntropyValue = CalcEntropy(statNum[],statNum[]);
         }
         /// <summary>
         /// 统计各个样本集合中所包含的目标属性Yes或者No的数目
         /// </summary>
         public void CountTotalClass(DataTable samples,out int no,out int yes)
         {
             yes = no = ;
             foreach (DataRow aRow in samples.Rows)
             {
                 if ((string)aRow[mTargetAttribute] == "Yes")
                     yes++;
                 else if ((string)aRow[mTargetAttribute] == "No")
                     no++;
                 else
                     throw new Exception("出错！");
             }
         }
         /// <summary>
         /// 计算熵值
         /// </summary>
         /// <returns></returns>
         public double CalcEntropy(int no,int yes)
         {
             double entropy = ;
             double total = (double)(yes + no);
             double p = ;
             if (no != )
             {
                 p = no / total;
                 entropy += -p * Math.Log(p,);
             }
             if (yes != )
             {
                 p = yes / total;
                 entropy += -p * Math.Log(p, );
             }
             return entropy;
         }
         /// <summary>
         /// 该注释可能有问题，从属性中的样本集合中得到yes或者no的数目
         /// </summary>
         /// <param name="samples"></param>
         /// <param name="attribute"></param>
         /// <param name="value"></param>
         /// <param name="no"></param>
         /// <param name="yes"></param>
         public void GetValuesToAttribute(DataTable samples, Attribute attribute, string value, out int no, out int yes)
         {
             no = yes = ;
             foreach (DataRow row in samples.Rows)
             {
                 if ((string)row[attribute.AttributeName] == value)
                 {
                     if ((string)row[mTargetAttribute] == "No")
                     {
                         no++;
                     }
                     else if ((string)row[mTargetAttribute] == "Yes")
                     {
                         yes++;
                     }
                     else
                     {
                         throw new Exception("出错");
                     }
                 }
             }
         }
         /// <summary>
         /// 计算信息收益
         /// </summary>
         /// <param name="samples"></param>
         /// <param name="attribute"></param>
         /// <returns></returns>
         public double Gain(DataTable samples, Attribute attribute)
         {
             mTotal = samples.Rows.Count;
             string[] values=attribute.values;
             double sum=0.0;
             for (int i = ; i < values.Length; i++)
             {
                 int no, yes;
                 no = yes = ;
                 GetValuesToAttribute(samples,attribute,values[i],out no,out yes);
                 if (yes == (yes + no) || no == (yes + no))
                 {
                     sum += ;
                 }
                 else
                 {
                     sum += (double)(yes + no) / (double)mTotal * (-(double)yes / (double)(yes + no) * Math.Log(((double)yes / (double)(yes + no)), ) - (double)no / (double)(yes + no) * Math.Log(((double)no / (double)(yes + no)), ));
                 }
             }
             return SplitInfo(samples,mTargetAttribute)- sum;
         }
         /// <summary>
         /// 获得targetAttribute属性下的所有属性值
         /// </summary>
         /// <param name="samples"></param>
         /// <param name="targetAttribute"></param>
         /// <returns></returns>
         private ArrayList GetDistinctValues(DataTable samples, string targetAttribute)
         {
             ArrayList distinctValues = new ArrayList(samples.Rows.Count);
             foreach (DataRow row in samples.Rows)
             {
                 if (distinctValues.IndexOf(row[targetAttribute]) == -)
                     distinctValues.Add(row[targetAttribute]);
             }
             return distinctValues;
         }
         /// <summary>
         /// 按某个属性值计算该属性的熵值
         /// </summary>
         /// <param name="samples"></param>
         /// <param name="attribute"></param>
         /// <returns></returns>
         public double SplitInfo(DataTable samples, string attribute)
         {
             ArrayList values = GetDistinctValues(samples,attribute);
             for (int i = ; i < values.Count; i++)
             {
                 if (values[i] == null || (string)values[i] == "")
                 {
                     values.RemoveAt(i);
                 }
             }
             int[] count=new int[values.Count];
             for (int i = ; i < values.Count; i++)
             {
                 foreach (DataRow aRow in samples.Rows)
                 {
                     if ((string)aRow[attribute] == (string)values[i])
                         count[i]++;
                 }
             }
             double entropy = ;
             double total = samples.Rows.Count;
             double p = ;
             for (int i = ; i < values.Count; i++)
             {
                 if (count[i] != )
                 {
                     p = count[i] / total;
                     entropy += -p * Math.Log(p,);
                 }
             }
             return entropy;
         }
         /// <summary>
         /// 获得指定属性的信息增益率
         /// </summary>
         /// <param name="samples">样本集合</param>
         /// <param name="attribute"></param>
         /// <returns></returns>
         public double GainRatio(DataTable samples, Attribute attribute)
         {
             double splitInfoA = this.SplitInfo(samples,attribute.AttributeName);//计算各个属性的熵值
             double gainA = Gain(samples,attribute);//信息增益
             double gainRatioA = gainA / splitInfoA;
             return gainRatioA;
         }
     }
 }

构造决策树：

 public class DTree_ID3
    {
        private string mTargetAttribute = "result";
        public Entropy en = new Entropy();
        public TreeNode roots;
        /// <summary>
        /// 获得信息增益率最大的属性
        /// </summary>
        /// <param name="samples"></param>
        /// <param name="attributes"></param>
        /// <returns></returns>
        private Attribute getBestAttribute(DataTable samples,Attribute[] attributes)
        {
            double maxGain = 0.0;
            Attribute bestAttribute = null;
            foreach (Attribute attribute in attributes)
            {
                double aux = en.GainRatio(samples,attribute);
                if (aux > maxGain)
                {
                    maxGain = aux;
                    bestAttribute = attribute;
                }
            }
            return bestAttribute;
        }
        /// <summary>
        /// 判断样例集是否属于同一类，即该样例集是否是"纯"的，是则返回此属性值，否则返回Null
        /// </summary>
        /// <param name="samples"></param>
        /// <param name="targetAttribute"></param>
        /// <returns></returns>
        public string AllSamplesSameClass(DataTable samples, string targetAttribute)
        {
            DataRow row = samples.Rows[];
            string targetValue = (string)row[targetAttribute];
            for (int i = ; i < samples.Rows.Count; i++)
            {
                if (targetValue!=samples.Rows[i][targetAttribute].ToString())
                {
                    return null;
                }
            }
            return targetValue;
        }
        /// <summary>
        /// 获得属性的目标属性的值（解释有可能错误）
        /// </summary>
        /// <param name="samples"></param>
        /// <param name="targetAttribute"></param>
        /// <returns></returns>
        private ArrayList GetDistinctValues(DataTable samples, string targetAttribute)
        {
            ArrayList distinctValues = new ArrayList(samples.Rows.Count);
            foreach (DataRow row in samples.Rows)
            {
                if (distinctValues.IndexOf(row[targetAttribute]) == -)
                    distinctValues.Add(row[targetAttribute]);
            }
            return distinctValues;
        }
        /// <summary>
        ///
        /// </summary>
        /// <param name="samples"></param>
        /// <param name="targetAttribute"></param>
        /// <returns></returns>
        private object GetMostCommonValue(DataTable samples, string targetAttribute)
        {
            ArrayList distinctValues = GetDistinctValues(samples,targetAttribute);
            int[] count=new int[distinctValues.Count];
            foreach (DataRow row in samples.Rows)
            {
                int index = distinctValues.IndexOf(row[targetAttribute]);
                count[index]++;
            }
            int MaxIndex = ;
            int MaxCount = ;
            for (int i = ; i < count.Length; i++)
            {
                if (count[i] > MaxCount)
                {
                    MaxCount = count[i];
                    MaxIndex = i;
                }
            }
            return distinctValues[MaxIndex];
        }
        /// <summary>
        /// 构造决策树
        /// </summary>
        /// <param name="samples">样本集合</param>
        /// <param name="targetAttribute">目标属性</param>
        /// <param name="attributes">该样本所含的属性集合</param>
        /// <returns></returns>
        private TreeNode BuildTree(DataTable samples, string targetAttribute, Attribute[] attributes)
        {
            TreeNode temp = new TreeNode();
            //如果samples中的元祖是同一类C
            string c = AllSamplesSameClass(samples,targetAttribute);
            if (c != null)   //返回N作为叶节点，以类C标记
                return new TreeNode(new Attribute(c).AttributeName + c);

            //if attributes为空，then
            if (attributes.Length == )//返回N作为叶子节点，标记为D中的多数类，多数表决
            {
                return new TreeNode(new Attribute(GetMostCommonValue(samples,targetAttribute)).AttributeName);
            }
            //计算目标属性的熵值，即PlayGolf的熵值
            mTargetAttribute = targetAttribute;
            en.getEntropy(samples);
            //找出最好的分类属性，即信息熵最大的
            Attribute bestAttribute = getBestAttribute(samples,attributes);
            //标记为节点root
            DTreeNode root = new DTreeNode(bestAttribute);
            temp.Text = bestAttribute.AttributeName;

            DataTable aSample = samples.Clone();
            //为bestAttribute的每个输出value划分元祖并产生子树
            foreach (string value in bestAttribute.values)
            {
                aSample.Rows.Clear();
                //aSamples为满足输出value的集合，即一个划分（分支）
                DataRow[] rows = samples.Select(bestAttribute.AttributeName+"="+"'"+value+"'");
                foreach (DataRow row in rows)
                {
                    aSample.Rows.Add(row.ItemArray);
                }
                //删除划分属性
                ArrayList aArributes = new ArrayList(attributes.Length-);
                for (int i = ; i < attributes.Length; i++)
                {
                    if (attributes[i].AttributeName != bestAttribute.AttributeName)
                    {
                        aArributes.Add(attributes[i]);
                    }
                }
                //如果aSample为空，加一个树叶到节点N，标记为aSample中的多数类
                if (aSample.Rows.Count == )
                {
                    TreeNode leaf = new TreeNode();
                    leaf.Text = GetMostCommonValue(samples, targetAttribute).ToString() + "(" + value + ")";
                    temp.Nodes.Add(leaf);
                }
                else  //加一个由BulidTree(samples,targetAttribute,attributes)返回的节点到节点N
                {
                    DTree_ID3 dc3 = new DTree_ID3();
                    TreeNode ChildNode = dc3.BuildTree(aSample,targetAttribute,(Attribute[])aArributes.ToArray(typeof(Attribute)));
                    ChildNode.Text += "(" + value + ")";
                    temp.Nodes.Add(ChildNode);
                }
            }
            roots = temp;
            return temp;
        }
        public TreeNode MountTree(DataTable samples, string targetAttribute, Attribute[] attributes)
        {
            return BuildTree(samples, targetAttribute, attributes);
        }
    }