poj1189 简单dp

http://poj.org/problem?id=1189

Description

有一个三角形木板,竖直立放。上面钉着n(n+1)/2颗钉子，还有(n+1)个格子（当n=5时如图1）。每颗钉子和周围的钉子的距离都等于d，每一个格子的宽度也都等于d，且除了最左端和最右端的格子外每一个格子都正对着最以下一排钉子的间隙。 

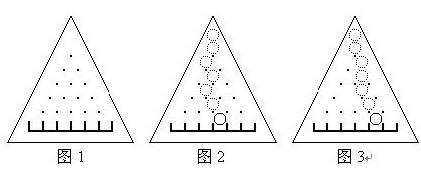
让一个直径略小于d的小球中心正对着最上面的钉子在板上自由滚落，小球每碰到一个钉子都可能落向左边或右边（概率各1/2）。且球的中心还会正对着下一颗将要碰上的钉子。比如图2就是小球一条可能的路径。 

我们知道小球落在第i个格子中的概率pi=pi=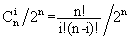，当中i为格子的编号，从左至右依次为0,1,...,n。 

如今的问题是计算拔掉某些钉子后，小球落在编号为m的格子中的概率pm。

假定最以下一排钉子不会被拔掉。比如图3是某些钉子被拔掉后小球一条可能的路径。 

Input

第1行为整数n（2 <= n <= 50）和m（0 <= m <= n）。下面n行依次为木板上从上至下n行钉子的信息，每行中'*'表示钉子还在，'.'表示钉子被拔去，注意在这n行中空格符可能出如今不论什么位置。

Output

仅一行，是一个既约分数(0写成0/1)，为小球落在编号为m的格子中的概pm。既约分数的定义：A/B是既约分数。当且仅当A、B为正整数且A和B没有大于1的公因子。

Sample Input

5 2
*
   * .
  * * *
 * . * *
* * * * *

Sample Output

7/16

/**
poj1189 简单dp
题目大意：又是中文题~
解题思路； 总共会出现2^n种情况，我们一開始就如果有2^n个球在(1,1)点往下落。

对于每个没有挖掉的钉子(i,j)：dp[i+1][j]+=dp[i][j]/2; dp[i+1][j+1]+=dp[i][j]/2;
           对于挖掉的钉子(i,j)：dp[i+2][j+1]+=dp[i][j];
*/
#include <stdio.h>
#include <string.h>
#include <algorithm>
#include <iostream>
using namespace std;
typedef long long LL;

bool a[2555];
int n,m;
LL dp[55][55];

LL gcd(LL x,LL y)
{
    if(y==0)return x;
    return gcd(y,x%y);
}

int main()
{
    while(~scanf("%d%d",&n,&m))
    {
        int k=1;
        for(int i=1; i<=n; i++)
        {
            for(int j=1; j<=i; j++)
            {
                char str[12];
                scanf("%s",str);
                if(str[0]=='*')
                {
                    a[k++]=true;
                }
                else
                {
                    a[k++]=false;
                }
                //printf("%d\n",a[k-1]);
            }
            //puts("");
        }
        memset(dp,0,sizeof(dp));
        dp[1][1]=1LL<<n;
        for(int i=1; i<=n; i++)
        {
            int x=i*(i-1)/2;
            for(int j=1; j<=i; j++)
            {
                if(a[j+x])
                {
                    dp[i+1][j]+=dp[i][j]/2;
                    dp[i+1][j+1]+=dp[i][j]/2;
                }
                else
                {
                    dp[i+2][j+1]+=dp[i][j];
                }
            }
        }
        LL x=1LL<<n;
        LL y=dp[n+1][m+1];
        LL g=gcd(x,y);
        printf("%lld/%lld\n",y/g,x/g);
    }
    return 0;
}