Sockets

Sockets

time limit per test

2 seconds

memory limit per test

256 megabytes

input

standard input

output

standard output

The ICM ACPC World Finals is coming! Unfortunately, the organizers of the competition were so busy preparing tasks that totally missed an important technical point — the organization of electricity supplement for all the participants workstations.

There are n computers for participants, the i-th of which has power equal to positive integer pi. At the same time there are m sockets available, the j-th of which has power euqal to positive integer sj. It is possible to connect the i-th computer to the j-th socket if and only if their powers are the same: pi = sj. It is allowed to connect no more than one computer to one socket. Thus, if the powers of all computers and sockets are distinct, then no computer can be connected to any of the sockets.

In order to fix the situation professor Puch Williams urgently ordered a wagon of adapters — power splitters. Each adapter has one plug and one socket with a voltage divider between them. After plugging an adapter to a socket with power x, the power on the adapter's socket becomes equal to 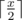, it means that it is equal to the socket's power divided by two with rounding up, for example  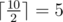and .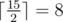

Each adapter can be used only once. It is possible to connect several adapters in a chain plugging the first to a socket. For example, if two adapters are plugged one after enother to a socket with power 10, it becomes possible to connect one computer with power 3 to this socket.

The organizers should install adapters so that it will be possible to supply with electricity the maximum number of computers c at the same time. If there are several possible connection configurations, they want to find the one that uses the minimum number of adapters u to connect c computers.

Help organizers calculate the maximum number of connected computers c and the minimum number of adapters u needed for this.

The wagon of adapters contains enough of them to do the task. It is guaranteed that it's possible to connect at least one computer.

Input

The first line contains two integers n and m (1 ≤ n, m ≤ 200 000) — the number of computers and the number of sockets.

The second line contains n integers p1, p2, ..., pn (1 ≤ pi ≤ 109) — the powers of the computers.

The third line contains m integers s1, s2, ..., sm (1 ≤ si ≤ 109) — the power of the sockets.

Output

In the first line print two numbers c and u — the maximum number of computers which can at the same time be connected to electricity and the minimum number of adapters needed to connect c computers.

In the second line print m integers a1, a2, ..., am (0 ≤ ai ≤ 109), where ai equals the number of adapters orginizers need to plug into the i-th socket. The sum of all ai should be equal to u.

In third line print n integers b1, b2, ..., bn (0 ≤ bi ≤ m), where the bj-th equals the number of the socket which the j-th computer should be connected to. bj = 0 means that the j-th computer should not be connected to any socket. All bj that are different from 0 should be distinct. The power of the j-th computer should be equal to the power of the socket bj after plugging in abj adapters. The number of non-zero bj should be equal to c.

If there are multiple answers, print any of them.

Examples

input

2 2
1 1
2 2

output

2 2
1 1
1 2

input

2 1
2 100
99

output

1 6
6
1 0
分析：按转换器个数排序模拟即可，能插则插，否则/2上取整放回去；
代码：

#include <iostream>
#include <cstdio>
#include <cstdlib>
#include <cmath>
#include <algorithm>
#include <climits>
#include <cstring>
#include <string>
#include <set>
#include <map>
#include <unordered_map>
#include <queue>
#include <stack>
#include <vector>
#include <list>
#define rep(i,m,n) for(i=m;i<=n;i++)
#define rsp(it,s) for(set<int>::iterator it=s.begin();it!=s.end();it++)
#define mod 1000000007
#define inf 0x3f3f3f3f
#define vi vector<int>
#define pb push_back
#define mp make_pair
#define fi first
#define se second
#define ll long long
#define pi acos(-1.0)
#define pii pair<int,int>
#define Lson L, mid, ls[rt]
#define Rson mid+1, R, rs[rt]
#define sys system("pause")
const int maxn=2e5+;
using namespace std;
ll gcd(ll p,ll q){return q==?p:gcd(q,p%q);}
ll qpow(ll p,ll q){ll f=;while(q){if(q&)f=f*p;p=p*p;q>>=;}return f;}
inline ll read()
{
    ll x=;int f=;char ch=getchar();
    while(ch<''||ch>''){if(ch=='-')f=-;ch=getchar();}
    while(ch>=''&&ch<=''){x=x*+ch-'';ch=getchar();}
    return x*f;
}
int n,m,k,t,p[maxn],s[maxn],vis[maxn],vis1[maxn],used[maxn],c,u;
queue<pii>pq;
set<pii>q;
int main()
{
    int i,j;
    scanf("%d%d",&n,&m);
    rep(i,,n)scanf("%d",&p[i]),q.insert(mp(p[i],i));
    rep(i,,m)scanf("%d",&s[i]),pq.push(mp(s[i],i));
    while(!pq.empty())
    {
        pii x=pq.front();
        pq.pop();
        bool flag=false;
        auto it=q.lower_bound(mp(x.fi,));
        if(it!=q.end()&&it->fi==x.fi)
        {
            vis[it->se]=x.se;
            vis1[x.se]=it->se;
            flag=true;
            q.erase(it);
        }
        if(!flag)
        {
            if(x.fi!=)
            {
                if(x.fi&)x.fi++;
                x.fi>>=;
                used[x.se]++;
                pq.push(mp(x.fi,x.se));
            }
        }
    }
    rep(i,,n)if(vis[i])c++;
    rep(i,,m)if(vis1[i])u+=used[i];
    printf("%d %d\n",c,u);
    rep(i,,m)
    {
        if(vis1[i])printf("%d ",used[i]);
        else printf("0 ");
    }
    printf("\n");
    rep(i,,n)printf("%d ",vis[i]);
    printf("\n");
    //system("Pause");
    return ;
}