bzoj3884上帝与集合的正确用法

Description

 

根据一些书上的记载，上帝的一次失败的创世经历是这样的：

第一天， 上帝创造了一个世界的基本元素，称做“元”。

第二天， 上帝创造了一个新的元素，称作“α”。“α”被定义为“元”构成的集合。容易发现，一共有两种不同的“α”。

第三天， 上帝又创造了一个新的元素，称作“β”。“β”被定义为“α”构成的集合。容易发现，一共有四种不同的“β”。

第四天， 上帝创造了新的元素“γ”，“γ”被定义为“β”的集合。显然，一共会有16种不同的“γ”。

如果按照这样下去，上帝创造的第四种元素将会有65536种，第五种元素将会有2^65536种。这将会是一个天文数字。

然而，上帝并没有预料到元素种类数的增长是如此的迅速。他想要让世界的元素丰富起来，因此，日复一日，年复一年，他重复地创造着新的元素……

然而不久，当上帝创造出最后一种元素“θ”时，他发现这世界的元素实在是太多了，以致于世界的容量不足，无法承受。因此在这一天，上帝毁灭了世界。

至今，上帝仍记得那次失败的创世经历，现在他想问问你，他最后一次创造的元素“θ”一共有多少种？

上帝觉得这个数字可能过于巨大而无法表示出来，因此你只需要回答这个数对p取模后的值即可。

你可以认为上帝从“α”到“θ”一共创造了10^9次元素，或10^18次，或者干脆∞次。

 

一句话题意：

Input

 

接下来T行，每行一个正整数p，代表你需要取模的值

Output

T行，每行一个正整数，为答案对p取模后的值

Sample Input

3
2
3
6

Sample Output

0
1
4

HINT

对于100%的数据，T<=1000,p<=10^7

 

Source

By PoPoQQQ

诶。。

真是一道神题。。

看起来很难。。

其实并不难。。

首先沃萌要知道一个东西：

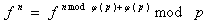
那么。。

设f[n]就是所求的东西。。

那么。。

ans=2^(f[phi[p]]+phi[p])%p

递归求f就行了。。

听说每次暴力求phi更快？！。

#include <cstdio>
using namespace std;
typedef long long ll;
int i,j,k,n,m,x,y,t,T,p,phi[],prime[],b[];
ll mi(int x,int y,int p){if (y==)return ;if (y==)return x%p;ll t=mi(x,y>>,p);t=(t*t)%p;return y&?(t*x)%p:t;}
ll solve(int p){if (p==)return ;return mi(,solve(phi[p])+phi[p],p);}
void pre(){
    for (i=;i<=;i++){
        if (!b[i]){prime[++prime[]]=i;phi[i]=i-;}
        for (j=;j<=prime[prime[]]&&i*prime[j]<=;j++){
            b[i*prime[j]]=;if (i%prime[j]==){phi[i*prime[j]]=phi[i]*prime[j];break;}phi[i*prime[j]]=phi[i]*(prime[j]-);
        }
    }
}
int main(){scanf("%d",&T);pre();while (T--){scanf("%d",&p);printf("%lld\n",solve(p));}}