MT【108】线面角最小

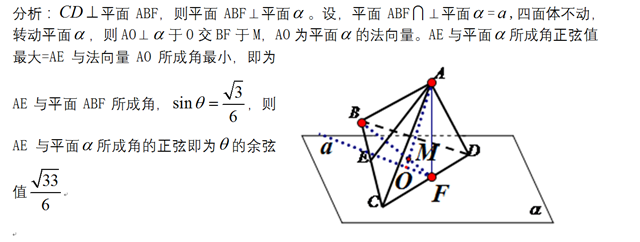
评:线面角最小,在此类最值中经常用到,作为选择填空可以投机.
MT【108】线面角最小的更多相关文章
- MT【118】利用线面角最小解题
解:如图将正四面体放到立方体中,让AB通过$\alpha$面,让$\alpha$面绕着AB动起来.问题就转化成为EF与面$\alpha$线面角$\theta$了.EF的投影为$|EF|cos\thet ...
- MT【109】线面角最大时为二面角平面角
解答:如图设C到$\alpha$面的距离为$d_1,C_1$到虚线距离为$d_2$ 所求距离$d=d_1+d_2=|AC|sin\theta+|CC_1|cos\theta=4\sqrt{2}sin\ ...
- MT【14】最大最小问题变形
解答: 评:这类最大最小问题有几何方法和代数方法两种解法.
- MT【179】最大最小老问题
求$\max\{x^2+2y+20,y^2-6x+12\}$的最小值______ 提示:$4t\ge 3(x^2+2y+20)+y^2-6x+12=3(x-1)^2+(y+3)^2+60\ge 60, ...
- MT【305】丹德林双球
如图.在正方体$ABCD-A_1B_1C_1D_1$中,点$M,N$分别是直线$CD,AB$上的动点,点$P$是$\Delta A_1C_1D_1$内的动点(不包括边界),记直线$DP$与$MN$所成 ...
- MT【193】三面角的正余弦定理
(原题为浙江名校新高考研究联盟2018届第三次联考选择压轴题) 在平面$\alpha$内,已知$AB\perp BC$,过直线$AB,BC$分别作平面$\beta,\gamma$,使得锐二面角$\al ...
- MT【52】空间法向量理解直线条数
[从最简单的做起.]--波利亚 评:线面角转化成线与线的角,这道题还有类似的这类题是学生的难点.
- highstock K线图 深入研究
K线图,相信每个股民都不陌生,如何用SVG画好一个K线图是一个难题. 我选择用highstock做为画图组件,适当的修改了一下源码,参考了数个财经网站的案例,完成了一个不太成熟的K线图,欢迎大家批评指 ...
- K-means的缺点(优化不仅仅是最小化误差)
K-means的缺点(优化不仅仅是最小化误差) #转载时,请注明英文原作David Robinson,译者Ding Chao.# 我最近遇到一个交叉验证的问题,我认为这个给我提供了一个很好的机会去用“ ...
随机推荐
- day05今日学习总结:字符串类型
昨日学习复习: 数据类型: 有序.无序 有序:可以根据索引查找的数据 可变不可变 可变:在值变的情况下,id不变,证明原值是在改变的 不可变:在值变的情况下,id也跟着变,证明不是在改原值. 今日学习 ...
- 第18章 SysTick—系统定时器
第18章 SysTick—系统定时器 全套200集视频教程和1000页PDF教程请到秉火论坛下载:www.firebbs.cn 野火视频教程优酷观看网址:http://i.youku.com/ ...
- Delphi 10.3 Rio + iOS 12.1 SDK 编译错误 "libcharset.1.dylib"
环境版本: Delphi 10.3 Rio iOS 12.1 SDK Xcode 10.1 (10B61) 错误讯息:[DCC Error] E2597 ld: file not found: /us ...
- 2017-2018-2 20155203《网络对抗技术》 Exp7:网络欺诈防范
1.基础问题回答 (1)通常在什么场景下容易受到DNS spoof攻击 连接无线网络,和恶意攻击者处在同一局域网下. (2)在日常生活工作中如何防范以上两攻击方法 首先决不去点击浏览器都认为不安全的网 ...
- 20155323刘威良《网络对抗》Exp8 Web基础
20155323刘威良<网络对抗>Exp8 Web基础 实践内容 (1).Web前端HTML(0.5分) 能正常安装.启停Apache.理解HTML,理解表单,理解GET与POST方法,编 ...
- Python基础(条件判断和循环) if elif else for while break continue;
条件判断 计算机之所以能做很多自动化的任务,因为它可以自己做条件判断. 比如,输入用户年龄,根据年龄打印不同的内容,在Python程序中,用if语句实现: age = 20 if age >= ...
- [agc011C]Squared Graph-[二分图]
Description 传送门 Solution 我们以下考虑的情况都是原图中非孤立的点. 题目要求新图的连通块个数.这个不好算,我们考虑计算新图的联通块内的特征点(x,y),即无法通过移动找到(t, ...
- lm393
电压比较芯片,供电电压和输出电压一致.
- docker之compose 编排项目
一.docker-compose 的介绍 docker-compose是一种容器编排工具,可以将多个docker容器关联部署.通过yaml文件,可以描述应用的架构,如使用什么镜像.数据卷.网络.绑定服 ...
- Outlook2013修改数据文件默认存放目录
转载 当使用outlook 2013新建Email账户的时候,其数据文件(.ost文件)总是被保存在C盘默认目录“C:\Users\用户名\AppData\Local\Microsoft\Outloo ...
