JDK源码那些事儿之PriorityBlockingQueue
今天继续说一说阻塞队列的实现，今天的主角就是优先级阻塞队列PriorityBlockingQueue，从命名上看觉得应该是有序的，毕竟是优先级队列，那么实际上是什么情况，我们一起看下其内部实现，提前说明下，因为PriorityBlockingQueue涉及到了堆排序的相关使用，如果没了解清楚，可以参考我之前写的关于堆排序的相关说明
前言
JDK版本号：1.8.0_171
PriorityBlockingQueue是一个无限容量的阻塞队列，当然，最终还是受内存限制，内部实现是数组，不停增长下去会导致OOM，由于其无限容量的特性，在入队操作时不存在阻塞这个说法，只要内存足够都能入队，当然，入队操作线程还是需要争抢互斥锁的，只是不会存在队列已满情况下的阻塞等待操作
同时，虽然这个被称为优先级阻塞队列，但是入队操作之后并不会立即进行排序调整，只有在出队操作或drainTo转移队列时才是被优先级队列排过序的。PriorityBlockingQueue是通过Comparator来进行排序，所以入队的对象本身已经实现Comparator接口，或者传入一个Comparator实例对象才可以
PriorityBlockingQueue排序是通过最小堆实现的，之前的文章里我已经专门说明了堆排序的算法，这里不再详细说明，不明白的可以先去参考堆排序的讲解部分。优先级队列初始容量默认为11，当入队空间不足时会进行扩容操作，扩容大小根据扩容前的容量决定
类定义
public class PriorityBlockingQueue<E> extends AbstractQueue<E>
implements BlockingQueue<E>, java.io.Serializable
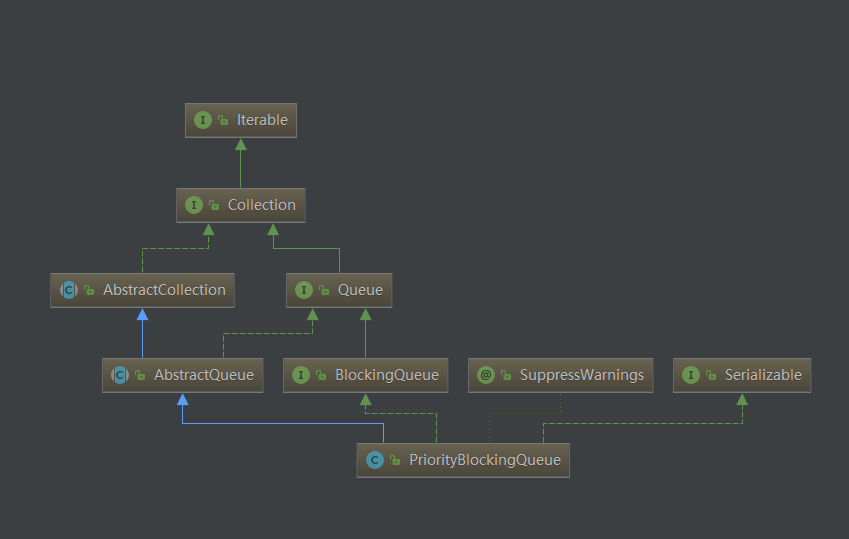
常量/变量
/**
* 默认初始化数组长度11
*/
private static final int DEFAULT_INITIAL_CAPACITY = 11;
/**
* 允许的最大数组长度，减8是因为有可能部分虚拟机会用一部分空间来保存对象头信息
*/
private static final int MAX_ARRAY_SIZE = Integer.MAX_VALUE - 8;
/**
*
* 优先级队列通过平衡二叉堆实现，可类比堆排序算法
* 那么queue[n]对应的左右子节点分别为queue[2*n+1]和[2*(n+1)]
* 队列中的对象必须是可比较的，默认的自然排序或自行实现的的Comparator都可
* 队列非空，则queue[0]为最小值，即以最小二叉堆排序
*/
private transient Object[] queue;
/**
* 优先级队列queue包含的元素个数
*/
private transient int size;
/**
* 比较器对象，在使用自然排序比较时为null
*/
private transient Comparator<? super E> comparator;
/**
* 互斥锁，只有一个ReentrantLock
*/
private final ReentrantLock lock;
/**
* 非空信号量，队列为空时阻塞出队线程
* 只需要判断队列为空的情况，队列没有满的情况，所以才是无限容量队列
*/
private final Condition notEmpty;
/**
* Spin锁，通过CAS操作实现
*/
private transient volatile int allocationSpinLock;
/**
* 在序列化中使用，为了兼容老版本
*/
private PriorityQueue<E> q;
allocationSpinLock在对象中的内存偏移量获取在静态代码块中实现如下，后续使用CAS操作用到
// Unsafe mechanics
private static final sun.misc.Unsafe UNSAFE;
private static final long allocationSpinLockOffset;
static {
try {
UNSAFE = sun.misc.Unsafe.getUnsafe();
Class<?> k = PriorityBlockingQueue.class;
allocationSpinLockOffset = UNSAFE.objectFieldOffset
(k.getDeclaredField("allocationSpinLock"));
} catch (Exception e) {
throw new Error(e);
}
}
构造方法
在不传参时，默认初始化数组长度为11，即优先级队列默认容量为11，主要在于传入集合参数时需要进行判断是否满足PriorityBlockingQueue使用的条件，非空，可比较的对象，另外，还需判断是否需要进行堆化操作
public PriorityBlockingQueue() {
this(DEFAULT_INITIAL_CAPACITY, null);
}
public PriorityBlockingQueue(int initialCapacity) {
this(initialCapacity, null);
}
public PriorityBlockingQueue(int initialCapacity,
Comparator<? super E> comparator) {
if (initialCapacity < 1)
throw new IllegalArgumentException();
this.lock = new ReentrantLock();
this.notEmpty = lock.newCondition();
this.comparator = comparator;
this.queue = new Object[initialCapacity];
}
public PriorityBlockingQueue(Collection<? extends E> c) {
this.lock = new ReentrantLock();
this.notEmpty = lock.newCondition();
// 是否需要重新排序标识，即堆化标识
boolean heapify = true; // true if not known to be in heap order
// 空值检查标识
boolean screen = true; // true if must screen for nulls
// 集合为SortedSet，则使用其Comparator排序，由于其已有序，直接复制即可，无需堆化操作
if (c instanceof SortedSet<?>) {
SortedSet<? extends E> ss = (SortedSet<? extends E>) c;
this.comparator = (Comparator<? super E>) ss.comparator();
heapify = false;
}
// 集合为PriorityBlockingQueue，则使用其Comparator排序
else if (c instanceof PriorityBlockingQueue<?>) {
PriorityBlockingQueue<? extends E> pq =
(PriorityBlockingQueue<? extends E>) c;
this.comparator = (Comparator<? super E>) pq.comparator();
screen = false;
// 精确到PriorityBlockingQueue类，由于其已有序，直接复制即可，无需堆化操作
if (pq.getClass() == PriorityBlockingQueue.class) // exact match
heapify = false;
}
Object[] a = c.toArray();
int n = a.length;
// If c.toArray incorrectly doesn't return Object[], copy it.
// 假如没有正确返回Object[]，则复制a
if (a.getClass() != Object[].class)
a = Arrays.copyOf(a, n, Object[].class);
// 对集合进行空值校验
// this.comparator != null 判断SortedSet类型的对象空值情况
// n == 1 这个感觉应该是对自然排序的对象做的操作 n >= 1 才对，否则就在heapify()堆化操作比较时抛错，可以自己尝试放List
if (screen && (n == 1 || this.comparator != null)) {
for (int i = 0; i < n; ++i)
if (a[i] == null)
throw new NullPointerException();
}
this.queue = a;
this.size = n;
// 堆化操作
if (heapify)
heapify();
}
重要方法
tryGrow
扩容操作，在offer中获取锁的时候调用，扩容之前先释放锁，通过CAS操作将allocationSpinLock标识置为1，表示当前正在扩容中，扩容完毕则重新获取锁，allocationSpinLock标识置为0
private void tryGrow(Object[] array, int oldCap) {
// 先释放锁
lock.unlock(); // must release and then re-acquire main lock
// 准备的新数组
Object[] newArray = null;
// 其他线程未进行扩容操作时尝试使用CAS更新allocationSpinLock标识为1，成功则当前线程取得扩容操作权限
if (allocationSpinLock == 0 &&
UNSAFE.compareAndSwapInt(this, allocationSpinLockOffset,
0, 1)) {
try {
// 原数组容量小于64，则每次增长oldCap + 2
// 原数组容量大于等于64，则每次增长oldCap的一半
int newCap = oldCap + ((oldCap < 64) ?
(oldCap + 2) : // grow faster if small
(oldCap >> 1));
// 新的数组容量大于最大的数组长度限制
if (newCap - MAX_ARRAY_SIZE > 0) { // possible overflow
int minCap = oldCap + 1;
// 原数组容量加1就已经溢出或者超过最大长度限制直接抛出OOM
if (minCap < 0 || minCap > MAX_ARRAY_SIZE)
throw new OutOfMemoryError();
// 设置新数组容量为最大值
newCap = MAX_ARRAY_SIZE;
}
// 扩容成功且当前数组没有被其他线程操作，则创建一个新数组
if (newCap > oldCap && queue == array)
newArray = new Object[newCap];
} finally {
// 将扩容标识恢复
allocationSpinLock = 0;
}
}
// 其他线程已经在扩容了，让出cpu
if (newArray == null) // back off if another thread is allocating
Thread.yield();
// 重新获得锁
lock.lock();
// 扩容成功且原数组没被其他线程操作则复制原数组到新数组中
if (newArray != null && queue == array) {
queue = newArray;
System.arraycopy(array, 0, newArray, 0, oldCap);
}
}
siftUpComparable/siftUpUsingComparator
类似堆排序的操作，不同在于，这些方法是类比插入新节点，即数组中添加新的值时调用，添加完之后整个堆需要进行调整，Up也说明了是从下往上进行堆的平衡调整。在调用这个方法前，堆应该是已经平衡的，如果未平衡，需要先进行堆化操作，参考heapify方法。入队操作时，将x插入k的位置上，入队时相当于将新元素放入k的位置上(还未完全执行，需要满足堆特性)，由于新添加元素可能会破坏整个堆，所以需要从下往上调整整个堆，直到x大于等于其父节点或者到达根节点
/**
* @param k the position to fill
* @param x the item to insert
* @param array the heap array
*/
private static <T> void siftUpComparable(int k, T x, Object[] array) {
Comparable<? super T> key = (Comparable<? super T>) x;
while (k > 0) {
// 找到k位置处的父节点
int parent = (k - 1) >>> 1;
// 父节点对应的值
Object e = array[parent];
// 父子节点比较，k位置处的节点大于等于其父节点，则退出，不需要对堆进行调整了
if (key.compareTo((T) e) >= 0)
break;
// k位置处的节点小于其父节点，则将k位置处的值改为其父节点值
array[k] = e;
// k指向其父节点，相当于堆向上递进了一层，继续while判断其父节点是否需要调整
k = parent;
}
// 结束调整时k指向的位置即为插入x的值，即key
array[k] = key;
}
/**
* 同上，区别在于这个使用了一个比较对象cmp，上边是自然排序
*/
private static <T> void siftUpUsingComparator(int k, T x, Object[] array,
Comparator<? super T> cmp) {
while (k > 0) {
int parent = (k - 1) >>> 1;
Object e = array[parent];
if (cmp.compare(x, (T) e) >= 0)
break;
array[k] = e;
k = parent;
}
array[k] = x;
}
siftDownComparable/siftDownUsingComparator
出队操作时使用，出队出的是堆顶元素，即array[0]，那么出队完成之后堆顶元素空缺，将array[n]处的元素放入位置0处（还未真正执行，需要先验证是否满足堆特性），这里翻译说的是插入，可以这么理解，出队时相当于将最后一个叶子节点移动到根（堆顶位置），这里就需要从上往下调整整个堆，使其满足堆的特性，这里按小顶堆处理，最上边则是最小值，需满足节点值小于其两个子节点的值即可
/**
* @param k the position to fill
* @param x the item to insert
* @param array the heap array
* @param n heap size
*/
private static <T> void siftDownComparable(int k, T x, Object[] array,
int n) {
if (n > 0) {
Comparable<? super T> key = (Comparable<? super T>)x;
// 最后的非叶子节点位置
int half = n >>> 1; // loop while a non-leaf
while (k < half) {
// k的左子节点
int child = (k << 1) + 1; // assume left child is least
// k的左子节点对应的值
Object c = array[child];
// k的右子节点
int right = child + 1;
// 左右子节点中最大值
if (right < n &&
((Comparable<? super T>) c).compareTo((T) array[right]) > 0)
c = array[child = right];
// 对比，其节点值小于等于其左右子节点，则表明堆调整完毕
if (key.compareTo((T) c) <= 0)
break;
// k节点处的值为其子节点中最大的值
array[k] = c;
// k指向其子节点最大值的那个索引位置
k = child;
}
// 结束调整时k指向的位置即为插入x的值，即key
array[k] = key;
}
}
/**
* 同上，区别在于这个使用了一个比较对象cmp，上边是自然排序
*/
private static <T> void siftDownUsingComparator(int k, T x, Object[] array,
int n,
Comparator<? super T> cmp) {
if (n > 0) {
int half = n >>> 1;
while (k < half) {
int child = (k << 1) + 1;
Object c = array[child];
int right = child + 1;
if (right < n && cmp.compare((T) c, (T) array[right]) > 0)
c = array[child = right];
if (cmp.compare(x, (T) c) <= 0)
break;
array[k] = c;
k = child;
}
array[k] = x;
}
}
dequeue
出队核心操作，需要先获取互斥锁才能执行，出队元素为array[0]节点，出队之后进行堆排序的操作，步骤如下：
- 保存array[n]值为x，清除数组中n处的值
- 通过siftDownComparable方法将x插入0（即堆顶位置）处操作
- siftDownComparable自身向下依次去进行整个堆的平衡调整
- 堆（数组）长度-1
private E dequeue() {
// 当前队列元素的长度
int n = size - 1;
// 无值 返回null
if (n < 0)
return null;
else {
Object[] array = queue;
// 保存堆顶元素array[0]
E result = (E) array[0];
// 保存最后一个元素
E x = (E) array[n];
// 置空清除最后一个元素
array[n] = null;
Comparator<? super E> cmp = comparator;
if (cmp == null)
// 通过自然排序使得整个堆保持小顶堆的特性，下面说
siftDownComparable(0, x, array, n);
else
// 通过传入的比较类对象排序使得整个堆保持小顶堆的特性
siftDownUsingComparator(0, x, array, n, cmp);
size = n;
return result;
}
}
heapify
堆化操作，从最后一个非叶子节点开始，循环对每个节点平衡，直到堆顶，完成堆的平衡操作
/**
* 构造方法传入集合时用到
* 将集合进行堆化操作，满足堆的特性
*/
private void heapify() {
Object[] array = queue;
int n = size;
// 最后一个非叶子节点
int half = (n >>> 1) - 1;
Comparator<? super E> cmp = comparator;
if (cmp == null) {
// 从最后一个非叶子节点开始调整
// 这里使用的是siftDownComparable，使得节点及其子节点满足堆特性
// 逐步向上遍历，最终使得整个数组满足堆特性
for (int i = half; i >= 0; i--)
siftDownComparable(i, (E) array[i], array, n);
}
else {
// 同上，多了个比较对象
for (int i = half; i >= 0; i--)
siftDownUsingComparator(i, (E) array[i], array, n, cmp);
}
}
offer
入队操作，最终都是调用offer，这里使用siftUpComparable从下向上调整，因为我们是将新值放到了队列最后，应向上进行调整
public boolean offer(E e) {
if (e == null)
throw new NullPointerException();
// 获得锁
final ReentrantLock lock = this.lock;
lock.lock();
int n, cap;
Object[] array;
// 数组容量不够时进行扩容操作，上边已经说过tryGrow这部分
while ((n = size) >= (cap = (array = queue).length))
tryGrow(array, cap);
try {
Comparator<? super E> cmp = comparator;
// 入队操作，将新节点放入最后，需要使用siftUpComparable从下往上进行调整
if (cmp == null)
siftUpComparable(n, e, array);
else
siftUpUsingComparator(n, e, array, cmp);
// 容量+1
size = n + 1;
// 队列有数据则唤醒阻塞的出队线程
notEmpty.signal();
} finally {
lock.unlock();
}
return true;
}
poll/take
出队操作，最终调用dequeue，上边已说过，其余部分同之前讲过的阻塞队列类似，不过多说明
public E poll() {
final ReentrantLock lock = this.lock;
lock.lock();
try {
return dequeue();
} finally {
lock.unlock();
}
}
public E take() throws InterruptedException {
final ReentrantLock lock = this.lock;
lock.lockInterruptibly();
E result;
try {
while ( (result = dequeue()) == null)
notEmpty.await();
} finally {
lock.unlock();
}
return result;
}
public E poll(long timeout, TimeUnit unit) throws InterruptedException {
long nanos = unit.toNanos(timeout);
final ReentrantLock lock = this.lock;
lock.lockInterruptibly();
E result;
try {
while ( (result = dequeue()) == null && nanos > 0)
nanos = notEmpty.awaitNanos(nanos);
} finally {
lock.unlock();
}
return result;
}
removeAt
删除队列中的某个元素，remove和removeEQ方法也是使用这个方法来进行操作的。这里有个地方需要注意下，在删除非最后一个节点时需要进行堆调整，把最后一个节点当成新值添加到删除位置，先通过siftDownComparable/siftDownUsingComparator向下进行平衡调整，如果没有进行调整，则需要调用siftUpComparable/siftUpUsingComparator向上进行调整，有些人可能不是很明白，其实想下堆的特性就能了解，在数组中并不是完全有序的，在最小堆中只要满足父节点小于等于其子节点即可，所以这里在注释上我也进行了说明，如果向下调整了，则i处的子节点取代了i，原来i处的节点一定大于等于i的父节点，所以i的子节点也大于等于i的父节点，不需要向上调整了。例如下图这种情况，就需要继续向上调整：
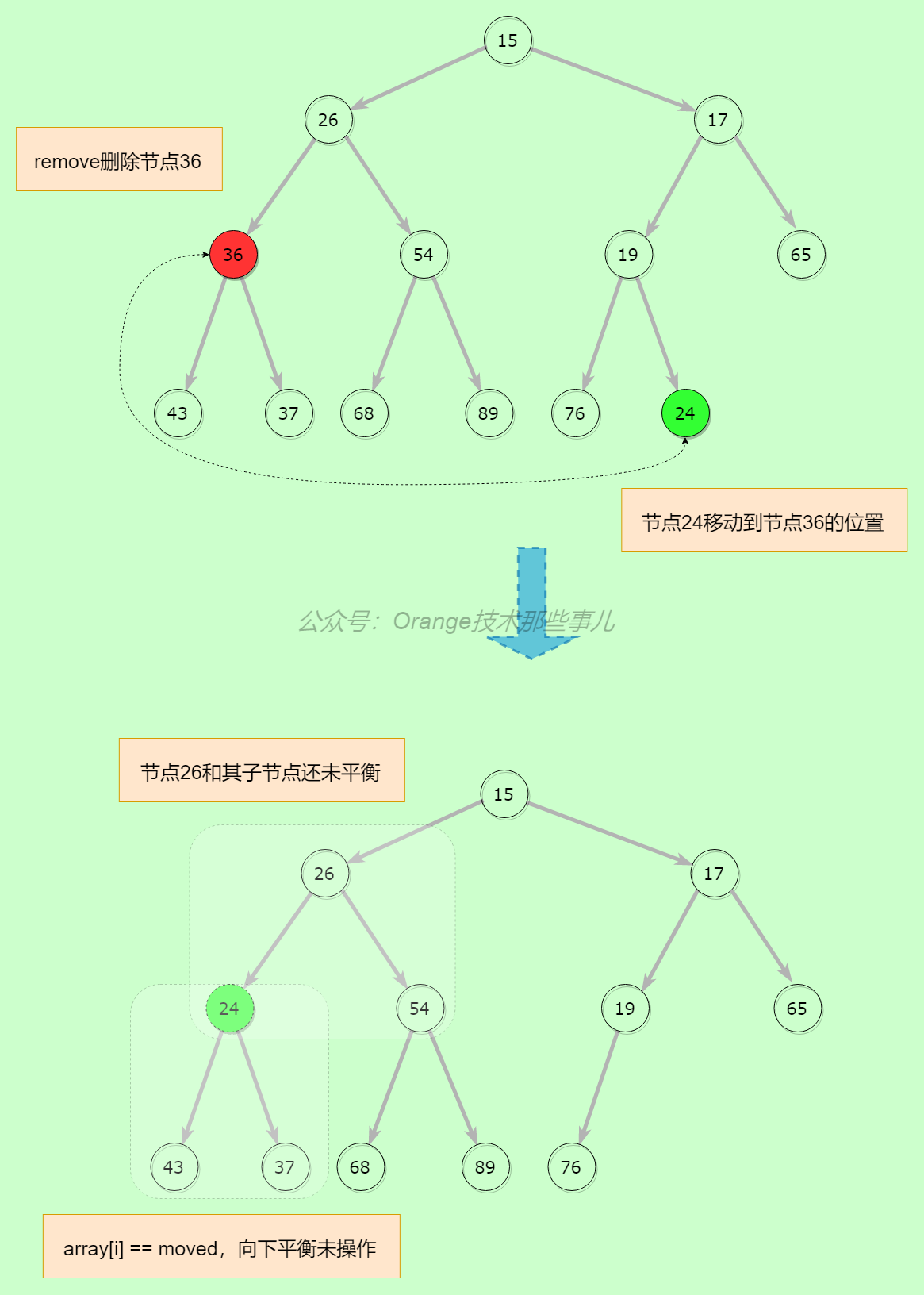
在删除36节点后，如果把24节点放入删除后的节点上，此时会导致array[i] == moved，需要向上调整，其实也是因为堆的特性导致，堆只保证了堆顶元素的有序性，其他元素如果调整则需要重新进行平衡操作
private void removeAt(int i) {
Object[] array = queue;
int n = size - 1;
// 移除最后一个节点，不需要调整堆
if (n == i) // removed last element
array[i] = null;
else {
// 下面相当于删除队列中间某个节点进行的操作
// 类似出队操作，只不过现在不一定是堆顶
E moved = (E) array[n];
array[n] = null;
Comparator<? super E> cmp = comparator;
if (cmp == null)
// 相当于将n处的节点放入删除的节点位置i处，之后向下进行堆化平衡操作
siftDownComparable(i, moved, array, n);
else
siftDownUsingComparator(i, moved, array, n, cmp);
// 向下无平衡操作，则需向上进行堆化平衡操作
// 如果向下调整了，则i处的子节点取代了i，原来i处的节点一定大于等于i的父节点，所以i的子节点也大于等于i的父节点
if (array[i] == moved) {
if (cmp == null)
siftUpComparable(i, moved, array);
else
siftUpUsingComparator(i, moved, array, cmp);
}
}
size = n;
}
drainTo
转移maxElements个元素到集合c中，从源码实现上可以看到转移之后的元素是有序的，而不是像PriorityBlockingQueue里的数组是无序的，每次转移，先直接添加堆顶元素，再出队操作，循环调用使得转移后的集合有序
public int drainTo(Collection<? super E> c, int maxElements) {
if (c == null)
throw new NullPointerException();
if (c == this)
throw new IllegalArgumentException();
if (maxElements <= 0)
return 0;
final ReentrantLock lock = this.lock;
lock.lock();
try {
// 集合长度
int n = Math.min(size, maxElements);
for (int i = 0; i < n; i++) {
// 先添加
c.add((E) queue[0]); // In this order, in case add() throws.
// 出队操作，堆已平衡
dequeue();
}
return n;
} finally {
lock.unlock();
}
}
迭代器
迭代器使用时的方法如下,每次调用创建一个新的迭代器对象Itr，入参调用了toArray()方法，拷贝了当前数组队列，不是直接放入的原数组队列
public Iterator<E> iterator() {
return new Itr(toArray());
}
public Object[] toArray() {
final ReentrantLock lock = this.lock;
lock.lock();
try {
return Arrays.copyOf(queue, size);
} finally {
lock.unlock();
}
}
看下其迭代器实现类，保存的是当前数组的一个拷贝，但是remove操作是删除的PriorityBlockingQueue原数组中对应的元素，需要注意
/**
* 迭代器，其中的数组是拷贝了当前数组的快照
*/
final class Itr implements Iterator<E> {
// 数组，这里保存的其实是原数组的快照，参考迭代调用方法
final Object[] array; // Array of all elements
// 游标，下一次next执行时对应的值的索引
int cursor; // index of next element to return
// 上一个next元素索引值，即上一次next()执行返回的那个值的索引，无则为-1
int lastRet; // index of last element, or -1 if no such
// 获取迭代器时调用，看上边源码
Itr(Object[] array) {
lastRet = -1;
this.array = array;
}
public boolean hasNext() {
return cursor < array.length;
}
public E next() {
// 游标指向已超过数组长度，抛错
if (cursor >= array.length)
throw new NoSuchElementException();
// 更新lastRet，记录next值索引
lastRet = cursor;
// 返回next应该获取的值，同时游标索引+1
return (E)array[cursor++];
}
public void remove() {
// 无值抛错
if (lastRet < 0)
throw new IllegalStateException();
// 这里调用removeEQ方法进行移除操作，注意，这里删除的是PriorityBlockingQueue的原数组中对应的值，不是这个拷贝数组
removeEQ(array[lastRet]);
// 置为-1
lastRet = -1;
}
}
迭代器是原数组的一个快照版本，故也是无序的，如果想通过迭代器获取有序数组是不可能的，同时，使用时需要注意remove方法，避免误删
总结
至此，PriorityBlockingQueue源码基本说明完毕，需要理解的在于以下几点：
- PriorityBlockingQueue是一个数组实现的无限制容量的优先级阻塞队列
- 默认初始容量为11，容量不够时可进行扩容操作
- 通过平衡二叉最小堆实现优先级排列
- take、poll方法出队或drainTo转移的集合才是有序的
以上内容如有问题欢迎指出，笔者验证后将及时修正，谢谢
JDK源码那些事儿之PriorityBlockingQueue的更多相关文章
- JDK源码那些事儿之并发ConcurrentHashMap上篇
前面已经说明了HashMap以及红黑树的一些基本知识,对JDK8的HashMap也有了一定的了解,本篇就开始看看并发包下的ConcurrentHashMap,说实话,还是比较复杂的,笔者在这里也不会过 ...
- JDK源码那些事儿之红黑树基础下篇
说到HashMap,就一定要说到红黑树,红黑树作为一种自平衡二叉查找树,是一种用途较广的数据结构,在jdk1.8中使用红黑树提升HashMap的性能,今天就来说一说红黑树,上一讲已经给出插入平衡的调整 ...
- JDK源码那些事儿之浅析Thread上篇
JAVA中多线程的操作对于初学者而言是比较难理解的,其实联想到底层操作系统时我们可能会稍微明白些,对于程序而言最终都是硬件上运行二进制指令,然而,这些又太过底层,今天来看一下JAVA中的线程,浅析JD ...
- JDK源码那些事儿之DelayQueue
作为阻塞队列的一员,DelayQueue(延迟队列)由于其特殊含义而使用在特定的场景之中,主要在于Delay这个词上,那么其内部是如何实现的呢?今天一起通过DelayQueue的源码来看一看其是如何完 ...
- JDK源码那些事儿之ConcurrentLinkedDeque
非阻塞队列ConcurrentLinkedQueue我们已经了解过了,既然是Queue,那么是否有其双端队列实现呢?答案是肯定的,今天就继续说一说非阻塞双端队列实现ConcurrentLinkedDe ...
- JDK源码那些事儿之ConcurrentLinkedQueue
阻塞队列的实现前面已经讲解完毕,今天我们继续了解源码中非阻塞队列的实现,接下来就看一看ConcurrentLinkedQueue非阻塞队列是怎么完成操作的 前言 JDK版本号:1.8.0_171 Co ...
- JDK源码那些事儿之LinkedBlockingDeque
阻塞队列中目前还剩下一个比较特殊的队列实现,相比较前面讲解过的队列,本文中要讲的LinkedBlockingDeque比较容易理解了,但是与之前讲解过的阻塞队列又有些不同,从命名上你应该能看出一些端倪 ...
- JDK源码那些事儿之LinkedTransferQueue
在JDK8的阻塞队列实现中还有两个未进行说明,今天继续对其中的一个阻塞队列LinkedTransferQueue进行源码分析,如果之前的队列分析已经让你对阻塞队列有了一定的了解,相信本文要讲解的Lin ...
- JDK源码那些事儿之SynchronousQueue上篇
今天继续来讲解阻塞队列,一个比较特殊的阻塞队列SynchronousQueue,通过Executors框架提供的线程池cachedThreadPool中我们可以看到其被使用作为可缓存线程池的队列实现, ...
随机推荐
- 大师Geoff Hinton关于Deep Neural Networks的建议
大师Geoff Hinton关于Deep Neural Networks的建议 Note: This covers suggestions from Geoff Hinton's talk given ...
- LeetCode 144. 二叉树的前序遍历(Binary Tree Preorder Traversal)
144. 二叉树的前序遍历 144. Binary Tree Preorder Traversal 题目描述 给定一个二叉树,返回它的 前序 遍历. LeetCode144. Binary Tree ...
- C++ 获取系统当前时间(日历时)
获取系统当前时间(日历时) //Linux & C++11 #include <chrono> #include <ctime> using namespace std ...
- 18 COUNTIF函数
求大于小于等于某个数字的数字有多少 格式:=COUNTIF(数据区,"条件") 注意条件需要用英文双引号引起来. 举个例子: =COUNTIF(A2:D5,">20 ...
- WUSTOJ 1333: Sequential game（Java）
题目链接:1333: Sequential game Description Sequential detector is a very important device in Hardware ex ...
- C++语言动态创建对象
焦头烂额的考试月终于过去了,终于有时间能停下来思考记录一下这一个月学过的东西,首先先总结一下,在自己仿写魂斗罗游戏时遇见的问题之一,人物在移动的时候如何去判断什么时候掉入水中显示水中画面,什么时候敌人 ...
- docker xfs卡死
原因 docker在xfs文件系统中,过于频繁create/destory container.pull/push image,当thin pool满时,DeviceMapper后端默认文件系统xfs ...
- Vue.js 2.x 混入
Vue.js 2.x mixins 混入 混入(mixins)是一种分发vue组件中可复用功能的非常灵活的方式.混入对象可以包含任意组件选项.当组件使用混入对象时,所有混入对象的选项将被混入该组件本身 ...
- docker第二章--数据管理
- 上传图片，图片过大压缩处理以及解决自拍时会出现图片横屏的bug修复、长按保存图片
js部分:module.exports = { resize: function (file, callback, options) { //配置 options = Object.assign({ ...