HDU 5884 Sort ——（K叉哈夫曼树）

　　这题真心比较奥义，先见这个人的博客：http://blog.csdn.net/libin66/article/details/52565484

　　补0的方法是使得其满足成为满K叉树，而其博客中所说的“所以当(n-1)%(k-1)!=0的时候，会出现归并不能最大化个数的情况，这样会影响二分的单调性”我作如下的解释：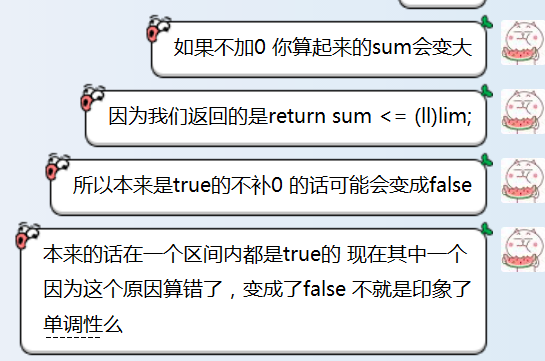

　　至于为什么不加0，sum会变大呢？作如下的解释：因为有一次合并不是最大个数的话，与其让它在后面单独合并增加权值还不如在前面补0合并呢，毕竟我们在算k的时候sum越小越好嘛~

　　原先代码如下（WA）：

 #include <stdio.h>
 #include <algorithm>
 #include <string.h>
 #include <queue>
 using namespace std;
 const int N =  + ;
 typedef long long ll;

 int n,lim;
 int a[N];

 bool can(int k)
 {
     if(k == ) return false;
     queue<ll> Q1,Q2;
     ll sum = ;
     for(int i=;i<=n;i++) Q1.push((ll)a[i]);
     while(Q1.size()+Q2.size() > )
     {
         if(Q1.size()+Q2.size() >= k)
         {
             ll temp = ;
             for(int i=;i<=k;i++)
             {
                 if(Q2.size()==)
                 {
                     temp += Q1.front();Q1.pop();
                 }
                 else if(Q1.size()==)
                 {
                     temp += Q2.front();Q2.pop();
                 }
                 else if(Q1.front()<=Q2.front())
                 {
                     temp += Q1.front();Q1.pop();
                 }
                 else
                 {
                     temp += Q2.front();Q2.pop();
                 }
             }
             sum += temp;
             Q2.push(temp);
         }
         else
         {
             ll temp = ;
             while(!Q1.empty())
             {
                 temp += Q1.front();Q1.pop();
             }
             while(!Q2.empty())
             {
                 temp += Q2.front();Q2.pop();
             }
             sum += temp;
         }
     }
     return sum <= (ll)lim;
 }

 int main()
 {
     int T;scanf("%d",&T);
     while(T--)
     {
         scanf("%d%d",&n,&lim);
         for(int i=;i<=n;i++) scanf("%d",a+i);
         sort(a+,a++n);
         int L = , R = n;
         int ans = ;
         while(L <= R)
         {
             //printf("!! %d %d\n",L,R);
             int mid = L + R >> ;
             if(can(mid))
             {
                 ans = mid;
                 R = mid - ;
             }
             else L = mid + ;
         }
         printf("%d\n",ans);
     }
     return ;
 }

 /*
     6
     6   120
     10 10 10 10 10
 */

WA的代码

　　AC代码如下：

 #include<iostream>
 //#include<bits/stdc++.h>
 #include<cstdio>
 #include<string>
 #include<cstring>
 #include<map>
 #include<queue>
 #include<set>
 #include<stack>
 #include<ctime>
 #include<algorithm>
 #include<cmath>
 #include<vector>
 #define showtime fprintf(stderr,"time = %.15f\n",clock() / (double)CLOCKS_PER_SEC)
 #pragma comment(linker, "/STACK:1024000000,1024000000")
 using namespace std;
 typedef long long ll;
 typedef long long LL;
 #define MP make_pair
 #define PII pair<int,int>
 #define PLI pair<long long ,int>
 #define PFI pair<double,int>
 #define PLL pair<ll,ll>
 #define PB push_back
 #define F first
 #define S second
 #define lson l,mid,rt<<1
 #define rson mid+1,r,rt<<1|1
 #define debug cout<<"?????"<<endl;
 //freopen("1005.in","r",stdin);
 //freopen("data.out","w",stdout);
 const int INF = 0x7f7f7f7f;
 const double eps = 1e-;
 const int M =   + ;
 const int N =  +  ;
 const double PI = acos(-.);
 const double E = 2.71828182845904523536;
 const int MOD = ;
 typedef vector<ll> Vec;
 typedef vector<Vec> Mat;
 int T,n,a[ + ];
 ll m;
 bool ok(int k){
     queue<ll> q,p;
     int t = (n-) % (k-);
     // 每次减少k-1个数。一共要减少 (n-1) 个数。 还剩下几个数要和 0 一组了
     if(t != ) for(int i =  ; i < k - t -  ; i ++) q.push();
     for(int i =  ; i < n ; i ++) q.push(a[i]);

     ll ans = ;
     while(!q.empty() || !p.empty()){
         ll tmp = ;
         for(int i =  ; i < k ; i ++){
             if(!q.empty() && !p.empty()){
                 ll u = q.front() , v = p.front();
                 if(u < v) tmp += u , q.pop();
                 else tmp += v , p.pop();
             }else if(!q.empty()){
                 ll u = q.front(); q.pop();
                 tmp += u;
             }else if(!p.empty()){
                 ll v = p.front() ; p.pop();
                 tmp += v;
             }else break;
         }
         ans += tmp;
         if(q.empty() && p.empty()) break;
         p.push(tmp);
     }
     return ans <= m;
 }
 void solve(){
     int l =  , r = n;
     while(l < r){
         int m = (l+r)>>;
         if(ok(m)) r = m;
         else l = m + ;
     }
     cout << l << endl;
 }
 int main(){
     cin >> T;
     while(T --){
         cin >> n >> m;
         for(int i =  ; i < n ; i ++) scanf("%d",&a[i]);
         sort(a,a+n);
         solve();
     }
     return ;
 }

AC代码