一句话题解&&总结

CF79D Password：

差分。两点取反，本质是匹配！最短路+状压DP

取反是套路，匹配是发现可以把操作进行目的化和阶段化，从而第二次转化问题。

且匹配不会影响别的位置答案

sequence

计算最长极长段小于等于j的方案数

突破口是i，k总共对数nlogn级别，干掉j用组合意义大力推导

CF1062F Upgrading Cities

DAG考虑topo，关键性质：topo序队列中点两两不可达。只在队列长度<=2时候才关心。

CF1060F Shrinking Tree

考虑x是不是rt，要进行讨论的。考虑e什么时候合并，也是要讨论的。

x是不是rt就成了分界点。e什么时候合并也是关键点，这样才对son的子树内序列做出了限制。也才能用上dp[son]转移。

所以状态就直接记录还剩下多少个边没有合并，这些边都要注意是否有1/2的概率限制。而且还可知道之前放入了多少边，有助于组合数分配转移。

CF1009G Allowed Letters

贪心，后面有无解即可。完美匹配，Hall定理

[THUWC2017]随机二分图

考虑每个方案的出现概率和，f[S]进行记忆化爆搜。s偶数有用，状态数<=1e8

第2/3类边，看做独立的，再额外贡献+25%或者-25%的同时选择方案的系数。

拆边转化，然后同上！

【模板】第二类斯特林数·列

递推式：OGF，再不断迭代

根据定义：EGF，然后快速幂，

LOJ#6079. 「2017 山东一轮集训 Day7」养猫

k可重区间问题 的增强版：有上下界！

直接都选择s[i],然后再把一些调整到e[i]

考虑通过最大流的“最大”，使得至少每k个有me个e，也即选择少于k个，则不能保证流量最大

通过最大流的“上界”，限制每k个最多有k-ms个e

CF295E aroslav and Points

考虑每段的贡献，l*a*b,直接动态开点线段树维护∑l，∑al，∑bl，∑abl，pushup即可。答案就是∑abl

（不知为啥放到了图论专题）

CF1054F Electric Scheme

每行每列一条线，多于交点？每行每列点与点的间隔搞出来当做点，二分图，相交就inf连边，

CF757F Team Rocket Rises Again

最短路DAG+支配树

CF786E ALT

注意审题！所有守卫都要有一个狗！

所以直接最小割。连边倍增优化一下即可。

CF986F Oppa Funcan Style Remastered

转化为质因子的配凑，同余最短路！特判一些情况。

Atcoder某比赛题

给定p=1e6+3（一个质数），q(q<=1e5)次询问，每次给定n，d，x，求$Pi_{i=0}^{n-1}(x+i\times d)$

智商题

提出$d^n$，然后就是$d^n\times Pi_{i=0}^{n-1}(\frac{x}{d}+i)$

Atcoder Dark Horse

晋级的比拼是一个深度为n的满二叉树，1号获胜，当且到根路径的其余2^i(0<=i<=15)的分支最小值都不能是ai

都不能其实很难保证。考虑容斥。ai从大到小排序

f[i][s]，前i个ai，钦定了|s|个作为s这个集合的分支子树的最小值。转移时候，分配给若干比ai大的编号即可。

然后ans+=(-1)^|s|*f[n][s]*....进行容斥即可。

然后这个只是分组，再乘上2^n*((2^i)!)才是答案。

#include<bits/stdc++.h>
#define reg register int
#define il inline
#define fi first
#define se second
#define mk(a,b) make_pair(a,b)
#define numb (ch^'0')
#define pb push_back
#define solid const auto &
#define enter cout<<endl
#define pii pair<int,int>
using namespace std;
typedef long long ll;
template<class T>il void rd(T &x){
    char ch;x=;bool fl=false;while(!isdigit(ch=getchar()))(ch=='-')&&(fl=true);
    for(x=numb;isdigit(ch=getchar());x=x*+numb);(fl==true)&&(x=-x);}
template<class T>il void output(T x){if(x/)output(x/);putchar(x%+'');}
template<class T>il void ot(T x){if(x<) putchar('-'),x=-x;output(x);putchar(' ');}
template<class T>il void prt(T a[],int st,int nd){for(reg i=st;i<=nd;++i) ot(a[i]);putchar('\n');}
namespace Modulo{
const int mod=1e9+;
int ad(int x,int y){return (x+y)>=mod?x+y-mod:x+y;}
void inc(int &x,int y){x=ad(x,y);}
int mul(int x,int y){return (ll)x*y%mod;}
void inc2(int &x,int y){x=mul(x,y);}
int qm(int x,int y=mod-){int ret=;while(y){if(y&) ret=mul(x,ret);x=mul(x,x);y>>=;}return ret;}
}
using namespace Modulo;
namespace Miracle{
const int N=;
const int M=(<<)+;
int jie[M],inv[M];
int C(int n,int m){
    if(n<||m<||n<m) return ;
    return mul(jie[n],mul(inv[m],inv[n-m]));
}
int f[N][<<];
int n,m;
int a[N];
int sz[<<];
bool cmp(int x,int y){
    return x>y;
}
int main(){
    rd(n);rd(m);
    for(reg i=;i<=m;++i) rd(a[i]);
    sort(a+,a+m+,cmp);

    jie[]=;
    for(reg i=;i<=(<<n);++i) jie[i]=mul(jie[i-],i);
    inv[<<n]=qm(jie[<<n]);
    for(reg i=(<<n)-;i>=;--i) inv[i]=mul(inv[i+],i+);

    for(reg i=;i<(<<n);++i){
        sz[i]=sz[i>>]*+(i&);
    }

    f[][]=;
    for(reg i=;i<=m;++i){
        // cout<<"i "<<a[i]<<endl;
        for(reg s=;s<(<<n);++s){
            if(f[i-][s]==) continue;
            f[i][s]=ad(f[i][s],f[i-][s]);
            for(reg p=;p<n;++p){
                if(!((s>>p)&)){
                    // cout<<" fang "<<s<<" and "<<p<<" : "<<mul(f[i-1][s],C((1<<n)-a[i]-sz[s],(1<<p)-1))<<endl;
                    f[i][s|(<<p)]=ad(f[i][s|(<<p)],mul(f[i-][s],C((<<n)-a[i]-sz[s],(<<p)-)));
                    // cout<<"go "<<(s|(1<<p))<<" "<<f[i][s|(1<<p)]<<endl;
                }
            }
        }
    }
    ll ans=;
    for(reg s=;s<(<<n);++s){
        int tmp=f[m][s];
        // cout<<" s "<<s<<" tmp "<<tmp<<endl;
        int re=(<<n)-sz[s]-;
        for(reg p=;p<n;++p){
            if(!((s>>p)&)){
                tmp=mul(tmp,C(re,(<<p)));
                re-=(<<p);
            }
        }
        // cout<<" after "<<tmp<<endl;
        if(__builtin_popcount(s)&){
            tmp=mod-tmp;
        }
        ans=ad(ans,tmp);
    }
    // cout<<"ans1111 "<<ans<<endl;

    ans=mul(ans,(<<n));
    for(reg i=;i<n;++i){
        ans=mul(ans,jie[<<i]);
    }
    ot(ans);
    return ;
}

}
signed main(){
    Miracle::main();
    return ;
}

/*
   Author: *Miracle*
*/

AT2000 Leftmost Ball

考虑多少种最终序列，直接从构造最终序列入手。

其实，最终序列里，白色球是左括号，每个颜色第一次出现的位置是右括号。就是一个括号匹配

f[i][j]，后[i,n]里，j个右括号方案数，每填一个右括号，那么后面的k-2个球直接小球放盒子分配即可。

k=1特判。

至于为何是“后[i,n]”而不是前，因为这样放右括号时一定知道后面有多少个“盒子”

#include<bits/stdc++.h>
#define reg register int
#define il inline
#define fi first
#define se second
#define mk(a,b) make_pair(a,b)
#define numb (ch^'0')
#define pb push_back
#define solid const auto &
#define enter cout<<endl
#define pii pair<int,int>
using namespace std;
typedef long long ll;
template<class T>il void rd(T &x){
    char ch;x=;bool fl=false;while(!isdigit(ch=getchar()))(ch=='-')&&(fl=true);
    for(x=numb;isdigit(ch=getchar());x=x*+numb);(fl==true)&&(x=-x);}
template<class T>il void output(T x){if(x/)output(x/);putchar(x%+'');}
template<class T>il void ot(T x){if(x<) putchar('-'),x=-x;output(x);putchar(' ');}
template<class T>il void prt(T a[],int st,int nd){for(reg i=st;i<=nd;++i) ot(a[i]);putchar('\n');}
namespace Modulo{
const int mod=1e9+;
int ad(int x,int y){return (x+y)>=mod?x+y-mod:x+y;}
void inc(int &x,int y){x=ad(x,y);}
int mul(int x,int y){return (ll)x*y%mod;}
void inc2(int &x,int y){x=mul(x,y);}
int qm(int x,int y=mod-){int ret=;while(y){if(y&) ret=mul(x,ret);x=mul(x,x);y>>=;}return ret;}
}
using namespace Modulo;
namespace Miracle{
const int N=;
const int M=++N+N;
int n,k;
int f[][N];
int jie[M],inv[M];
int C(int n,int m){
    if(n<||m<||n<m) return ;
    return mul(jie[n],mul(inv[m],inv[n-m]));
}
int main(){
    rd(n);rd(k);
    if(k==){
        puts("");return ;
    }
    int lim=n*k+n+n;
    jie[]=;
    for(reg i=;i<=lim;++i) jie[i]=mul(jie[i-],i);
    inv[lim]=qm(jie[lim]);
    for(reg i=lim-;i>=;--i) inv[i]=mul(inv[i+],i+);
    int tmp=;
    f[][]=;
    for(reg i=*n;i>=;--i){
        tmp^=;
        memset(f[tmp],,sizeof f[tmp]);
        int re=*n-i;
        for(reg j=;j<=min(re,n);++j){
            if(!f[tmp^][j]) continue;
            int le=re-j;
            if(le+<=j) f[tmp][j]=ad(f[tmp][j],f[tmp^][j]);
            if(j!=n){
                f[tmp][j+]=ad(f[tmp][j+],mul(f[tmp^][j],C(k-+le+j*(k-),le+j*(k-))));
            }
        }
    }
    ll ans=mul(f[tmp][n],jie[n]);
    ot(ans);
    return ;
}

}
signed main(){
    Miracle::main();
    return ;
}

/*
   Author: *Miracle*
*/

AT3576 Popping Balls

好题！考虑蓝色球的放置，s和t的最优位置来统计每个方案

CF1169B Pairs

被B题干掉了。。。

其实很简单。如果存在(a,b),(c,d)四个数都不同的数对，必然决策是两个数对各选择一个。

如果不存在，那么意味着，选择(a,b)，剩下的都至少和a，b之一有交点，一定有解！

#include<bits/stdc++.h>
#define reg register int
#define il inline
#define fi first
#define se second
#define mk(a,b) make_pair(a,b)
#define numb (ch^'0')
#define pb push_back
#define solid const auto &
#define enter cout<<endl
#define pii pair<int,int>
using namespace std;
typedef long long ll;
template<class T>il void rd(T &x){
    char ch;x=;bool fl=false;while(!isdigit(ch=getchar()))(ch=='-')&&(fl=true);
    for(x=numb;isdigit(ch=getchar());x=x*+numb);(fl==true)&&(x=-x);}
template<class T>il void output(T x){if(x/)output(x/);putchar(x%+'');}
template<class T>il void ot(T x){if(x<) putchar('-'),x=-x;output(x);putchar(' ');}
template<class T>il void prt(T a[],int st,int nd){for(reg i=st;i<=nd;++i) ot(a[i]);putchar('\n');}
namespace Modulo{
const int mod=;
int ad(int x,int y){return (x+y)>=mod?x+y-mod:x+y;}
void inc(int &x,int y){x=ad(x,y);}
int mul(int x,int y){return (ll)x*y%mod;}
void inc2(int &x,int y){x=mul(x,y);}
int qm(int x,int y=mod-){int ret=;while(y){if(y&) ret=mul(x,ret);x=mul(x,x);y>>=;}return ret;}
}
//using namespace Modulo;
namespace Miracle{
const int N=3e5+;
int x[N],y[N];
int a,b,c,d;
int n,m;
bool che(int a,int b){
    for(reg i=;i<=m;++i){
        if(x[i]!=a&&x[i]!=b&&y[i]!=a&&y[i]!=b) return false;
    }
    return true;
}
int main(){
    rd(n);rd(m);
    for(reg i=;i<=m;++i){
        rd(x[i]);rd(y[i]);
    }
    a=x[],b=y[];
    for(reg i=;i<=m;++i){
        if(x[i]!=a&&x[i]!=b&&y[i]!=a&&y[i]!=b){
            c=x[i],d=y[i];
        }
    }
    if(che(a,b)||che(a,c)||che(a,d)||che(b,c)||che(b,d)) puts("YES");
    else puts("NO");
    return ;
}

}
signed main(){
    Miracle::main();
    return ;
}

/*
   Author: *Miracle*
*/

CF860E Arkady and a Nobody-men

同层的处理lca，dfs序排序后，lca深度单调！单调栈维护即可！

CF685B Kay and Snowflake

子树重心一定在重儿子子树内。不断往上爬直到合法。复杂度O(重链总长度)=O(n)

51nod1766

唉降智了。五级题都不会

点集到点集的最大值。边权为正数

一个常用的套路：一个树上点集的直径，可以直接合并两个集合得到。四个端点C(4,2)计算即可。

另一个常用套路：编号区间？线段树！线段树区间维护这个区间的直径两个端点即可。

注意，询问的时候不能从[a,b]和[c,d]内部取max

#include<bits/stdc++.h>
#define reg register int
#define il inline
#define fi first
#define se second
#define mk(a,b) make_pair(a,b)
#define numb (ch^'0')
#define pb push_back
#define solid const auto &
#define enter cout<<endl
#define pii pair<int,int>
using namespace std;
typedef long long ll;
template<class T>il void rd(T &x){
    char ch;x=;bool fl=false;while(!isdigit(ch=getchar()))(ch=='-')&&(fl=true);
    for(x=numb;isdigit(ch=getchar());x=x*+numb);(fl==true)&&(x=-x);}
template<class T>il void output(T x){if(x/)output(x/);putchar(x%+'');}
template<class T>il void ot(T x){if(x<) putchar('-'),x=-x;output(x);putchar(' ');}
template<class T>il void prt(T a[],int st,int nd){for(reg i=st;i<=nd;++i) ot(a[i]);putchar('\n');}
namespace Modulo{
const int mod=;
int ad(int x,int y){return (x+y)>=mod?x+y-mod:x+y;}
void inc(int &x,int y){x=ad(x,y);}
int mul(int x,int y){return (ll)x*y%mod;}
void inc2(int &x,int y){x=mul(x,y);}
int qm(int x,int y=mod-){int ret=;while(y){if(y&) ret=mul(x,ret);x=mul(x,x);y>>=;}return ret;}
}
//using namespace Modulo;
namespace Miracle{
const int N=+;
int n,m;
struct node{
    int nxt,to,val;
}e[*N];
int hd[N],cnt;
void add(int x,int y,int z){
    e[++cnt].nxt=hd[x];
    e[cnt].to=y;e[cnt].val=z;
    hd[x]=cnt;
}
int a[*N],dfn[N],lp;
int dep[N],dis[N];
int lg[*N];
int f[*N][];
void dfs(int x,int fa){
    dep[x]=dep[fa]+;
    a[++lp]=x;
    dfn[x]=lp;
    for(reg i=hd[x];i;i=e[i].nxt){
        int y=e[i].to;
        if(y==fa) continue;
        dis[y]=dis[x]+e[i].val;
        dfs(y,x);
        a[++lp]=x;
    }
}
int cmp(int x,int y){
    return dep[x]<dep[y]?x:y;
}
int lca(int x,int y){
    if(x==y) return x;
    x=dfn[x],y=dfn[y];
    if(x>y) swap(x,y);
    int len=lg[y-x+];
    return cmp(f[x][len],f[y-(<<len)+][len]);
}
int dist(int x,int y){
    return dis[x]+dis[y]-*dis[lca(x,y)];
}
struct tr{
    int p[];
    int mx;
    tr(){
        p[]=p[]=;mx=;
    }
}t[*N];
#define ls (x<<1)
#define rs (x<<1|1)
#define mid ((l+r)>>1)
tr merge(tr a,tr b){
    tr ret;
    if(a.mx>b.mx) ret=a;
    else ret=b;
    for(reg i=;i<=;++i){
        for(reg j=;j<=;++j){
            int lp=dist(a.p[i],b.p[j]);
            if(lp>ret.mx){
                ret.p[]=a.p[i],ret.p[]=b.p[j];ret.mx=lp;
            }
        }
    }
    return ret;
}
tr con(tr a,tr b){
    tr ret;
    for(reg i=;i<=;++i){
        for(reg j=;j<=;++j){
            int lp=dist(a.p[i],b.p[j]);
            if(lp>ret.mx){
                ret.p[]=a.p[i],ret.p[]=b.p[j];ret.mx=lp;
            }
        }
    }
    return ret;
}
void pushup(int x){
    t[x]=merge(t[ls],t[rs]);
}
void build(int x,int l,int r){
    if(l==r){
        t[x].p[]=t[x].p[]=l;t[x].mx=;return;
    }
    build(x<<,l,mid);
    build(x<<|,mid+,r);
    pushup(x);
}
tr query(int x,int l,int r,int L,int R){
    if(L<=l&&r<=R) return t[x];
    if(L>mid) return query(rs,mid+,r,L,R);
    if(R<=mid) return query(ls,l,mid,L,R);
    return merge(query(ls,l,mid,L,R),query(rs,mid+,r,L,R));
}
int main(){
    rd(n);
    int x,y,z;
    for(reg i=;i<n;++i){
        rd(x);rd(y);rd(z);
        add(x,y,z);add(y,x,z);
    }
    dfs(,);
    for(reg i=;i<=lp;++i){
        lg[i]=(i>>(lg[i-]+))?lg[i-]+:lg[i-];
        f[i][]=a[i];
    }
    for(reg j=;j<=;++j){
        for(reg i=;i+(<<j)-<=lp;++i){
            f[i][j]=cmp(f[i][j-],f[i+(<<(j-))][j-]);
        }
    }
    build(,,n);
    rd(m);
    int a,b,c,d;
    while(m--){
        rd(a);rd(b);rd(c);rd(d);
        tr k=con(query(,,n,a,b),query(,,n,c,d));
        printf("%d\n",k.mx);
    }
    return ;
}

}
signed main(){
    Miracle::main();
    return ;
}

/*
   Author: *Miracle*
*/

AT3912 Antennas on Tree

性质题，考虑k个点的连通块，当且仅当，连通块外的点形成若干条链且每个关键点最多与一个外部点相连。贪心即可。

51nod 1538

相当于一些球的序列，每种颜色的球有价值ai，价值总和是m的方案数

枚举最后一个球的颜色f[n]=∑f[n-ai]

线性递推即可。

CF643E Bear and Destroying Subtrees

emmm

f[x][i]表示x子树深度<=i的概率，$f[x][i]=\Pi0.5*(f[y][i-1]+1)$

精度<=1e-6,所以i只用记录到60即可，后面概率几乎为0

添加新点的时候暴力更新60个祖先。

#include<bits/stdc++.h>
#define reg register int
#define il inline
#define fi first
#define se second
#define mk(a,b) make_pair(a,b)
#define numb (ch^'0')
#define pb push_back
#define solid const auto &
#define enter cout<<endl
#define pii pair<int,int>
using namespace std;
typedef long long ll;
template<class T>il void rd(T &x){
    char ch;x=;bool fl=false;while(!isdigit(ch=getchar()))(ch=='-')&&(fl=true);
    for(x=numb;isdigit(ch=getchar());x=x*+numb);(fl==true)&&(x=-x);}
template<class T>il void output(T x){if(x/)output(x/);putchar(x%+'');}
template<class T>il void ot(T x){if(x<) putchar('-'),x=-x;output(x);putchar(' ');}
template<class T>il void prt(T a[],int st,int nd){for(reg i=st;i<=nd;++i) ot(a[i]);putchar('\n');}
namespace Modulo{
const int mod=;
il int ad(int x,int y){return x+y>=mod?x+y-mod:x+y;}
il int sub(int x,int y){return ad(x,mod-y);}
il int mul(int x,int y){return (ll)x*y%mod;}
il void inc(int &x,int y){x=ad(x,y);}
il void inc2(int &x,int y){x=mul(x,y);}
il int qm(int x,int y=mod-){int ret=;while(y){if(y&) ret=mul(x,ret);x=mul(x,x);y>>=;}return ret;}
template<class ...Args>il int ad(const int a,const int b,const Args &...args) {return ad(ad(a,b),args...);}
template<class ...Args>il int mul(const int a,const int b,const Args &...args) {return mul(mul(a,b),args...);}
}
// using namespace Modulo;
#define ld long double
namespace Miracle{
const int N=+;
const int M=;
int q,n;
ld f[N][];
int fa[N];
int main(){
    rd(q);
    int op,x;
    n=;f[n][]=;
    for(reg i=;i<=M;++i) f[n][i]=;
    while(q--){
        rd(op);rd(x);
        if(op==){
            ++n;fa[n]=x;
            for(reg i=;i<=M;++i) f[n][i]=;
            ld tp=f[x][];
            f[x][]*=0.5;
            int o=;
            int las=x;
            x=fa[x];

            while(x&&o<=M){
                ld lp=f[x][o];
                f[x][o]/=(0.5*tp+0.5);
                f[x][o]*=(0.5*f[las][o-]+0.5);
                las=x;
                tp=lp;
                x=fa[x];++o;
            }
        }else{
            ld ans=f[x][]*;
            for(reg i=;i<=M;++i){
                ans+=(f[x][i]-f[x][i-])*i;
            }
            double lp=ans;
            printf("%.10lf\n",lp);
        }
    }
    return ;
}

}
signed main(){
    Miracle::main();
    return ;
}

/*
   Author: *Miracle*
*/

取max期望，可以记录每个达到值的概率

开不下？保留60个。。。一种无聊也有用的trick

AT2705 Yes or No

决策只和当前对错剩下的个数大小关系有关，相同的时候随机选择。

等价于在图上走，在不同位置决策不同

而路径只和实际答案对错的排列有关。

每个路径概率都是一样的。

统计每个路径的答案和。

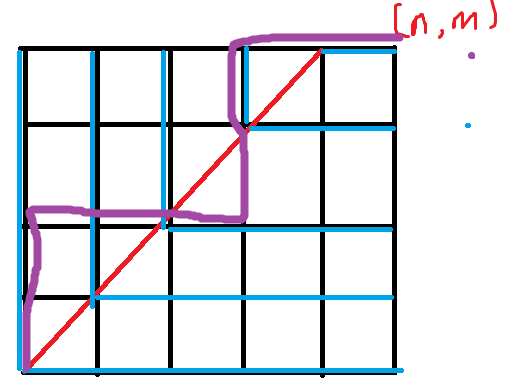
蓝色表示决策

不论对于什么路径，一定会覆盖max(n,m)个蓝色的段，至少是max(n,m)

对于y=x的，1/2概率正确。

统计所有路径经过y=x的次数的和。枚举每个(i,i)的点，统计经过的路径条数即可。

神奇

AT2062 ~K Perm Counting

容斥，统计至少j个不合法的

但是相差k是可能有冲突，所以每2×k个单独考虑

f[i][j][0/1]最后一个有没有选择上面的。类似分组背包做一下。

AT2370 Piling Up

naive地，设f[i][j]表示，剩下i轮，目前有j个白球所有方案数。

显然转移是横着走，往右下（白白），往右上（黑黑）三种。横着走可能有两种走法（白黑，黑白）

两个方案不同，当且仅当折线形状不同，或者横着走的两种走法选择不同。

会算重。

套路地，考虑在某个位置钦定统计：规定必须这个折线途中一次选择会使得白球个数为0

f[i][j][0/1]

转移即可。

tip：0/1是或的关系转移，用i-1更新i更好写。

（但我不是这样写的2333）

#include<bits/stdc++.h>
#define reg register int
#define il inline
#define fi first
#define se second
#define mk(a,b) make_pair(a,b)
#define numb (ch^'0')
#define pb push_back
#define solid const auto &
#define enter cout<<endl
#define pii pair<int,int>
using namespace std;
typedef long long ll;
template<class T>il void rd(T &x){
    char ch;x=;bool fl=false;while(!isdigit(ch=getchar()))(ch=='-')&&(fl=true);
    for(x=numb;isdigit(ch=getchar());x=x*+numb);(fl==true)&&(x=-x);}
template<class T>il void output(T x){if(x/)output(x/);putchar(x%+'');}
template<class T>il void ot(T x){if(x<) putchar('-'),x=-x;output(x);putchar(' ');}
template<class T>il void prt(T a[],int st,int nd){for(reg i=st;i<=nd;++i) ot(a[i]);putchar('\n');}
namespace Modulo{
const int mod=1e9+;
il int ad(int x,int y){return x+y>=mod?x+y-mod:x+y;}
il int sub(int x,int y){return ad(x,mod-y);}
il int mul(int x,int y){return (ll)x*y%mod;}
il void inc(int &x,int y){x=ad(x,y);}
il void inc2(int &x,int y){x=mul(x,y);}
il int qm(int x,int y=mod-){int ret=;while(y){if(y&) ret=mul(x,ret);x=mul(x,x);y>>=;}return ret;}
template<class ...Args>il int ad(const int a,const int b,const Args &...args) {return ad(ad(a,b),args...);}
template<class ...Args>il int mul(const int a,const int b,const Args &...args) {return mul(mul(a,b),args...);}
}
using namespace Modulo;
namespace Miracle{
const int N=;
int n,m;
int f[N][N][];
int main(){
    rd(n);rd(m);
    for(reg i=;i<=n;++i) f[][i][]=;
    for(reg i=;i<=m;++i){
        for(reg j=;j<=n;++j){
            inc(f[i][j][],ad((j!=n)*f[i-][j][],(j!=&&j!=)*f[i-][j][]));
            inc(f[i][j][],ad((j!=n)*f[i-][j][],(j!=)*f[i-][j][],(j==)*(f[i-][j][])));
            inc(f[i][j][],ad((j!=n)*f[i-][j+][],(j!=&&j!=)*f[i-][j-][]));
            inc(f[i][j][],ad((j!=n)*f[i-][j+][],(j!=)*f[i-][j-][],(j==)*f[i-][j-][]));
        }
    }
    int ans=;
    inc(f[m][][],f[m][][]);
    for(reg j=;j<=n;++j){
        inc(ans,f[m][j][]);
    }
    ot(ans);
    return ;
}

}
signed main(){
    Miracle::main();
    return ;
}

/*
   Author: *Miracle*
*/

TCO14 Wildcard CountTables

TCO14 Wildcard CountTables——斯特林数+容斥

[HEOI2013]ALO

我怎么这么zz啊

枚举次大值x,次大值存在于两个极长的区间,和左边第一个/第二个,右边第一个/第二个比x大的有关系.可以从小到大排序，链表维护前驱后继，删除。

可持久化trie即可.

[AGC031E]

https://atcoder.jp/contests/agc031/tasks/agc031_e

好题

如果x，y只有一个方向限制，那么两个链反着连边即可（前缀后缀）。

各有两个方向？

枚举一共选择k个

那么右侧<=lim等价于左侧>=k-lim

成功转化为一侧！

有源汇上下界最大费用最大流即可。

策略：沿着一个路一直走，如果碰到断边，直接走到T的最短路，代价是所有断边情况的最大值。

如果能处理好一条邻边断了的最短路，dijkstra类似的Dp转移即可。

带修最短路问题，考虑最短路树

一条邻边断了，一定是最短路树往子树走再出去。

可并堆。（或者二维数点也可以）