luogu3629

P3629 [APIO2010]巡逻

题目描述

在一个地区中有 n 个村庄，编号为 1, 2, ..., n。有 n – 1 条道路连接着这些村 庄，每条道路刚好连接两个村庄，从任何一个村庄，都可以通过这些道路到达其 他任一个村庄。每条道路的长度均为 1 个单位。 为保证该地区的安全，巡警车每天要到所有的道路上巡逻。警察局设在编号 为 1 的村庄里，每天巡警车总是从警察局出发，最终又回到警察局。 下图表示一个有 8 个村庄的地区，其中村庄用圆表示（其中村庄 1 用黑色的 圆表示），道路是连接这些圆的线段。为了遍历所有的道路，巡警车需要走的距 离为 14 个单位，每条道路都需要经过两次。

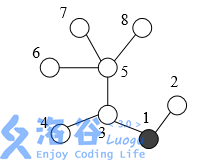
为了减少总的巡逻距离，该地区准备在这些村庄之间建立 K 条新的道路， 每条新道路可以连接任意两个村庄。两条新道路可以在同一个村庄会合或结束 （见下面的图例（c））。 一条新道路甚至可以是一个环，即，其两端连接到同一 个村庄。 由于资金有限，K 只能是 1 或 2。同时，为了不浪费资金，每天巡警车必须 经过新建的道路正好一次。 下图给出了一些建立新道路的例子：

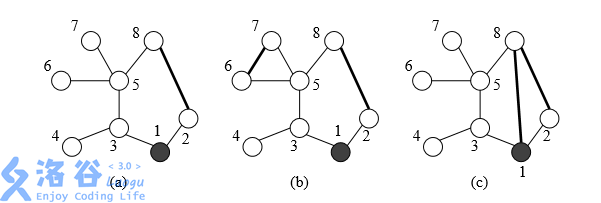
在(a)中，新建了一条道路，总的距离是 11。在(b)中，新建了两条道路，总 的巡逻距离是 10。在(c)中，新建了两条道路，但由于巡警车要经过每条新道路 正好一次，总的距离变为了 15。 试编写一个程序，读取村庄间道路的信息和需要新建的道路数，计算出最佳 的新建道路的方案使得总的巡逻距离最小，并输出这个最小的巡逻距离。

输入格式

第一行包含两个整数 n, K(1 ≤ K ≤ 2)。接下来 n – 1 行，每行两个整数 a, b， 表示村庄 a 与 b 之间有一条道路(1 ≤ a, b ≤ n)。

输出格式

输出一个整数，表示新建了 K 条道路后能达到的最小巡逻距离。

输入输出样例

输入 #1复制

8 1
1 2
3 1
3 4
5 3
7 5
8 5
5 6 

输出 #1复制

11

输入 #2复制

8 2
1 2
3 1
3 4
5 3
7 5
8 5
5 6 

输出 #2复制

10

输入 #3复制

5 2
1 2
2 3
3 4
4 5 

输出 #3复制

6

说明/提示

10%的数据中，n ≤ 1000, K = 1；

30%的数据中，K = 1；

80%的数据中，每个村庄相邻的村庄数不超过 25；

90%的数据中，每个村庄相邻的村庄数不超过 150； 100%的数据中，3 ≤ n ≤ 100,000, 1 ≤ K ≤ 2。

sol：一开始有一个很fp的idea(大雾，就是找到一条直径以后再找一条不重复的次长链，就被ztn用下面这样的树叉掉了%%%ztnakking

显然找到最长链以后应该把中间两条连起来最优，这样就是把之前的直径上的边边权改为-1，因为如果再走会对答案造成负贡献，之前其实已经减掉了，在减-1相当于+1，然后在用dp跑一遍直径就好了

#include <bits/stdc++.h>
using namespace std;
typedef int ll;
inline ll read()
{
    ll s=; bool f=; char ch=' ';
    while(!isdigit(ch)) {f|=(ch=='-'); ch=getchar();}
    while(isdigit(ch)) {s=(s<<)+(s<<)+(ch^); ch=getchar();}
    return (f)?(-s):(s);
}
#define R(x) x=read()
inline void write(ll x)
{
    if(x<) {putchar('-'); x=-x;}
    if(x<) {putchar(x+''); return;}
    write(x/); putchar((x%)+'');
}
#define W(x) write(x),putchar(' ')
#define Wl(x) write(x),putchar('\n')
const int N=,M=,inf=0x3f3f3f3f;
int n,k;
#define pii pair<int,int>
#define Mp make_pair
#define fi first
#define se second
pii rt1,rt2;
int tot=,Next[M],to[M],val[M],head[N],dep[N],fae[N],fa[N],dp[N][];
bool inq[N],Bo[N];
inline void Link(int x,int y,int z)
{
    Next[++tot]=head[x]; to[tot]=y; val[tot]=z; head[x]=tot;
}
inline pii bfs(int s)
{
    int i,dd=;
    queue<int>Que;
    memset(inq,,sizeof inq); fa[s]=; fae[s]=dep[s]=; Que.push(s); inq[s]=;
    while(!Que.empty())
    {
        int x=Que.front(); Que.pop(); if(dep[x]>dep[dd]) dd=x;
        for(i=head[x];i;i=Next[i]) if(!inq[to[i]])
        {
            fa[to[i]]=x; fae[to[i]]=i; dep[to[i]]=dep[x]+; inq[to[i]]=; Que.push(to[i]);
        }
    }
    return Mp(dd,dep[dd]);
}
inline void dfs(int x,int fat)
{
    int e;
    dp[x][]=dp[x][]=;
    for(e=head[x];e;e=Next[e]) if(to[e]!=fat)
    {
//        cout<<x<<' '<<to[e]<<' '<<val[e]<<endl;
        dfs(to[e],x);
        int tmp=dp[to[e]][]+val[e];
//        if(x==5) cout<<to[e]<<' '<<"tmp="<<tmp<<endl;
        dp[x][]=max(dp[x][],tmp+dp[x][]);
        dp[x][]=max(dp[x][],tmp);
    }
}
int main()
{
    int i,x,y,ans=-inf;
    R(n); R(k);
    for(i=;i<n;i++)
    {
        R(x); R(y); Link(x,y,); Link(y,x,);
    }
    rt1=bfs();
    rt2=bfs(rt1.fi);
    if(k==) Wl((n-)*-(rt2.se-));
    else
    {
        int oo=rt2.fi;
        while(oo!=rt1.fi)
        {
//            cout<<"oo="<<oo<<' '<<fa[oo]<<" "<<fae[oo]<<endl;
            val[fae[oo]]=val[(fae[oo]&)?(fae[oo]+):(fae[oo]-)]=-;
            oo=fa[oo];
        }
        dfs(rt1.fi,);
        for(i=;i<=n;i++)
        {
//            cout<<"i:"<<i<<' '<<dp[i][0]<<' '<<dp[i][1]<<endl;
            ans=max(ans,dp[i][]);
        }
        Wl((n-)*-(rt2.se-)-(ans-));
    }
    return ;
}
/*
input
8 1
1 2
3 1
3 4
5 3
7 5
8 5
5 6
output
11

input
8 2
1 2
3 1
3 4
5 3
7 5
8 5
5 6
output
10
*/