【模板】dijkstra与floyd

（我永远喜欢floyd）

温馨提示：与SPFA一起食用效果更佳

传送门：https://www.cnblogs.com/Daz-Os0619/p/11388157.html

Floyd

大概思路：

对于某两个点来说，查找他们之间是否连通，若连通，是记录他们间的最短路。

这里的最短路有两个方向：一个是直接到，一个是通过另外一个点到。（十分单纯的最短路了）

不需要多讲上代码！

void floyd() {
    for (int k = ; k <= n; ++k)
        for (int i = ; i <= n; ++i)
            for (int j = ; j <= n; ++j)
                dis[i][j] = min(dis[i][j], dis[i][k] + dis[k][j]);
}

Dijkstra

大概思路：

（跟SPFA差不多？？）

有一个集合P，一开始只有源点S在P中，每次更新都把集合之外路径值最小的一个放入集合中，更新与它相连的点，重复前面的操作直到集合外没有元素。

特殊要求：所有边权要是正的

这时的时间复杂度为O（n*n） （比较危险）

可以采用堆来优化 时间复杂度O（n*logn）

（蒟蒻发言：怎么用堆优化？）

堆

一颗完全二叉树。

这里用到的小根堆是最小值作为堆顶元素，大根堆反之。

大概长下面这样：

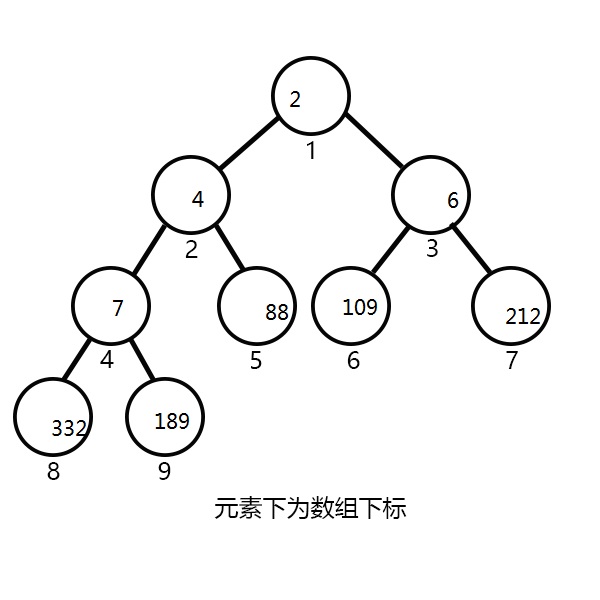
利用小根堆优化Dijkstra的理由与用SLF优化SPFA的理由相同，核心思想也相近，但是写法差异很大。

核心思想：因为每一次都会从队首开始遍历，当队首是最小值时，被更新的所以节点的值也会是最小值，这样可以节省很大一部分时间。

（这里就体现优先队列的好处）

下面是核心代码（可以先看注释，后面有图解）：

struct edges {
    int next, to, v;
    edges() {}
    edges(int _n, int _t, int _v) : next(_n), to(_t), v(_v) {}//next表示与这条边同起点的上一条边
} e[];

struct heap_node {
    int v, to;
    heap_node() {}
    heap_node(int _v, int _to) : v(_v), to(_to) {}
};
inline bool operator < (const heap_node &a, const heap_node &b) {
    return a.v > b.v; //这里实现的是小根堆，如果要大根堆，把 > 改成 < 即可
}

priority_queue <heap_node> h;

inline void add_to_heap(const int p) {
    for (int x = first[p]; x; x = e[x].next)//first表示以first为头的最后一条边
        if (dis[e[x].to] == -)//如果下一条边还没在堆里
            h.push(heap_node(e[x].v + dis[p], e[x].to));//加上前一个点的最短路值（跟新），放入堆
}

void Dijkstra(int S) {
    memset(dis, -, sizeof(dis));//清空（便于将数据放入堆里）
    while (!h.empty()) h.pop();//清空堆
    dis[S] = , add_to_heap(S);//现将所有与源点相连的点放入堆中
    int p;
    while (!h.empty()) { //堆空时所有的点都更新完毕（与SPFA相反）
        if (dis[h.top().to] != -)//如果与堆顶元素相连的点已经有了最短路值
         {
            h.pop();//弹掉堆顶 （此时堆顶不会被更新了）
            continue;//一直找到可以被更新的点
        }
        p = h.top().to;//找到与堆顶相连且不在堆里的点
        dis[p] = h.top().v;//更新最短路值（只是堆顶的）
        h.pop();//弹掉
        add_to_heap(p);//再更新与它相连的点，并将与它相连的点放入堆
    }
}

好长的注释啊。。

再画个图解释一下

（这里的样例和SPFA的样例一样）

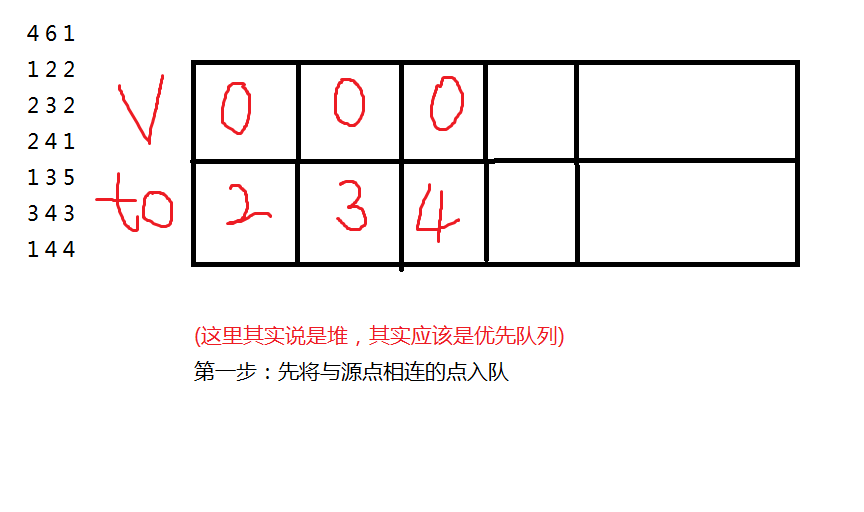
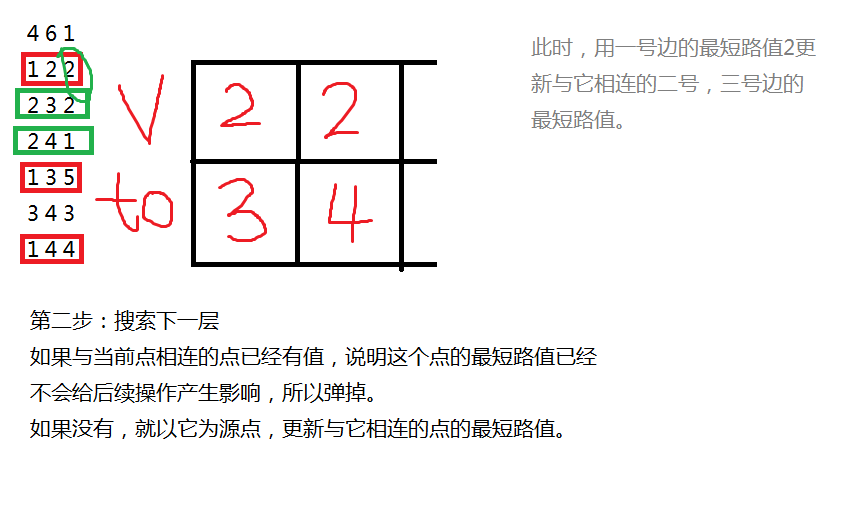
后面就这样一直循环直到队列为空。为空时所有最短路更新完毕。

完整代码：

#include<iostream>
#include<vector>
#include<queue>
#include<cstring>
#include<cstdio>
using namespace std;
struct edge
{
    int next,to,v;
    edge(){}
    edge(int a,int b,int c)
    {
        next=a;
        to=b;
        v=c;
    }
}E[];
int first[],n,dis[];
int S;
struct heap
{
    int to,v;
    heap(){}
    heap(int a,int b)
    {
        to=a;
        v=b;
    }
};
inline bool operator< (const heap &a,const heap &b)
{
    return    a.v>b.v;
}
priority_queue<heap> h;

void add_to_heap(int p)
{
    for(int i=first[p];i;i=E[i].next)
    {
        if(dis[E[i].to]==-)
        h.push(heap(E[i].to,dis[p]+E[i].v));
    }
}
int tot;
void add_edges(int a,int b,int c)
{
    E[++tot]=edge(first[a],b,c);
    first[a]=tot;
}
void dijkstra(int S)
{
    while(!h.empty())
    h.pop();
    memset(dis,-,sizeof(dis));
    dis[S]=;
    add_to_heap(S);
    int p;
    while(!h.empty())
    {
        if(dis[h.top().to]!=-)
        {
            h.pop();
            continue;
        }
        p=h.top().to;
        dis[p]=h.top().v;
        h.pop();
        add_to_heap(p);
    }
}
int m;
int main()
{
    cin>>n>>m>>S;
    int A,B,C;
    for(int i=;i<=m;i++)
    {
        cin>>A>>B>>C;
        add_edges(A,B,C);
    }
    dijkstra(S);
    for(int i=;i<=n;i++)
    cout<<dis[i]<<endl;
    return ;
}

结束！

今天也想放烟花！