luoguP3371 【模板】单源最短路径

P3371 【模板】单源最短路径

• • 3K通过
  • 10.7K提交
• 题目提供者 HansBug
• 标签 云端↑
• 难度 普及/提高-
• 时空限制 1s / 128MB

题目描述

如题，给出一个有向图，请输出从某一点出发到所有点的最短路径长度。

输入输出格式

输入格式：

第一行包含三个整数N、M、S，分别表示点的个数、有向边的个数、出发点的编号。

接下来M行每行包含三个整数Fi、Gi、Wi，分别表示第i条有向边的出发点、目标点和长度。

输出格式：

一行，包含N个用空格分隔的整数，其中第i个整数表示从点S出发到点i的最短路径长度（若S=i则最短路径长度为0，若从点S无法到达点i，则最短路径长度为2147483647）

输入输出样例

输入样例#1：

4 6 1
1 2 2
2 3 2
2 4 1
1 3 5
3 4 3
1 4 4

输出样例#1：

0 2 4 3

说明

时空限制：1000ms,128M

数据规模：

对于20%的数据：N<=5，M<=15

对于40%的数据：N<=100，M<=10000

对于70%的数据：N<=1000，M<=100000

对于100%的数据：N<=10000，M<=500000

样例说明：

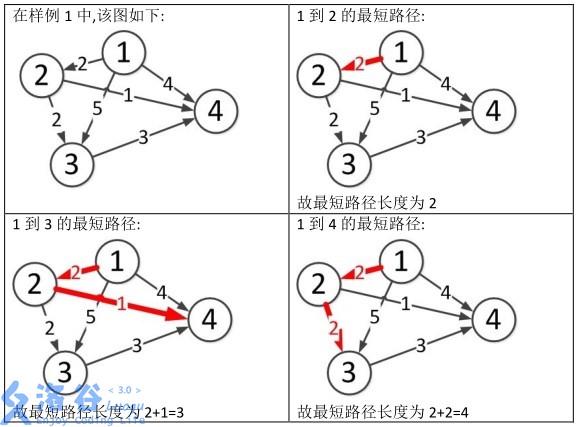
思路:

　　一看单源最短路！

　　我们可以想到两种：1）spfa

　　　　　　　　　　　2）dijkstra

坑点:

　　单纯的dijkstra是不能够AC的，需要用STL进行堆优化

上代码:

1）spfa:

#include <iostream>
#include <cstring>
#include <cstdio>
#include <cmath>
#include <queue>
using namespace std;

const int N = ;
const int M = ;
int n,m,s;
int h[N],top;
int dis[N];
bool vis[N];

struct E {
    int to,next,w;
}t[M];

void add(int u,int v,int w)
{
    t[++top].to=v;
    t[top].w=w;
    t[top].next=h[u];
    h[u]=top;
}

void spfa(int s)
{
    int u,v;
    queue<int>q;
    dis[s]=,vis[s]=;
    q.push(s);
    while(!q.empty())
    {
        u=q.front();
        q.pop();
        vis[u]=;
        for(int i=h[u];i!=-;i=t[i].next)
        {
            v=t[i].to;
            if(dis[u]+t[i].w<dis[v])
            {
                dis[v]=dis[u]+t[i].w;
                if(!vis[v])
                {
                    q.push(v);
                    vis[v]=;
                }
            }
        }
    }
    for(int i=;i<=n;i++)
        printf("%d ",dis[i]);
}

int main()
{
    scanf("%d%d%d",&n,&m,&s);
    for(int i=;i<=n;i++)
        h[i]=-,dis[i]=;
    for(int i=,u,v,w;i<=m;i++)
    {
        scanf("%d%d%d",&u,&v,&w);
        add(u,v,w);
    }
    spfa(s);
    return ;
}

---

 2）dijkstra

#include <iostream>
#include <cstdio>
#include <queue>
#define INF 2147483647
using namespace std;

typedef pair<int,int>p;
priority_queue< p,vector <p> ,greater <p> >q;
const int N = ;
const int M = ;
int n,m;
int h[N],top;
int dis[N];
bool vis[N];

struct E {
    int to,next,w;
}t[M];

void add(int u,int v,int w)
{
    t[++top].to=v;
    t[top].w=w;
    t[top].next=h[u];
    h[u]=top;
}

void dijkstra(int s)
{
    dis[s]=;
    q.push(make_pair(dis[s],s));
    while(!q.empty())
    {
        p tmp=q.top();
        q.pop();
        int u=tmp.second;
        if(vis[u])
            continue;
        vis[u]=true;
        for(int i=h[u];i!=-;i=t[i].next)
        {
            int v=t[i].to;
            if(dis[u]+t[i].w<dis[v])
            {
                dis[v]=dis[u]+t[i].w;
                q.push(make_pair(dis[v],v));
            }
        }
    }
    for(int i=;i<=n;i++)
        printf("%d ",dis[i]);
}

int main()
{
    int s;
    scanf("%d%d%d",&n,&m,&s);
    for(int i=;i<=n;i++)
        h[i]=-,dis[i]=INF;
    for(int i=,u,v,w;i<=m;i++)
    {
        scanf("%d%d%d",&u,&v,&w);
        add(u,v,w);
    }
    dijkstra(s);
    return ;
}