14 用DFT计算线性卷积

用DFT计算线性卷积

两有限长序列之间的卷积

我们知道，两有限长序列之间的卷积可以用圆周卷积代替，假设两有限长序列的长度分别为\(M\)和\(N\),那么卷积后的长度为\(L=M+N-1\),那么用圆周卷积计算线性卷积的具体过程为:

1. 首先将两序列在尾部补零，延拓成长度为L=M+N-1的序列
2. 将两序列进行圆周卷积，卷积后的结果即为线性卷积的结果

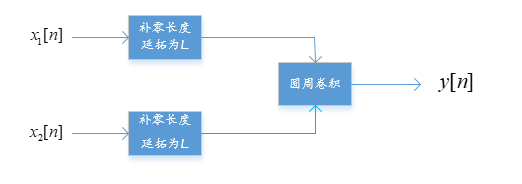
  而圆周卷积的实现可以通过下图实现

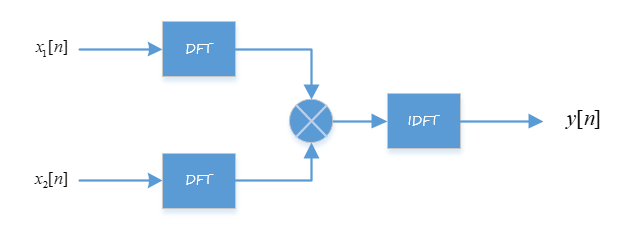
现讨论\(X[k]\)的\(IDFT\)使用\(DFT\)实现
\[
x[n]=\frac{1}{N}\sum_{n=0}^{N-1}X[k]W_N^{-kn}=\frac{1}{N}(\sum_{n=0}^{N-1}X^{*}[k]W_N^{kn})^{*}\rightarrow \frac{1}{N}(DFT\{X^{*}[k]\})^{*}
\]
上图可以改进为

所以线性卷积可以完全使用\(DFT\)实现，而\(DFT\)可以使用其快速算法\(FFT​\)大大降低计算量。

有限长序列与无限长序列卷积

或者说有限长序列与另一长度远大于其长度的序列进行卷积，如果按照上面直接用\(DFT\)计算的话，有两个问题。

1. 必须知道无限长序列的全部元素，才能进行计算
2. 用DFT计算卷积可能还不如直接进行卷积运算来得快

为解决上述的问题，可以将无限长序列划分为短序列，将短序列与有限长序列进行卷积，然后对结果进行处理，主要由两种方法:重叠相加法和重叠保留法。

重叠相加法

假设有限长序列\(h[n]\)的长度为\(M\),无限长序列\(x[n]\)将其以长度\(N\)进行分割，则
\[
x[n]=\sum_{m=-\infty}^{\infty}x_m[n-mN]
\]
其中
\[
x_m[n]=\begin{cases}
x[n+mN], &0 \leq n \leq N-1\\
0, &其他
\end{cases}
\]
\(x_m[n]\)表示将划分的第\(m\)段的起点移到原点。如下

则卷积
\[
\begin{aligned}
y[n]=h[n]*x[n]&=\sum_{l=-\infty}^{\infty}h[l]x[n-l]\\
&=\sum_{l=-\infty}^{\infty}h[l]\sum_{m=-\infty}^{\infty}x_m[n-l-mN]\\
&=\sum_{m=-\infty}^{\infty}\sum_{l=-\infty}^{\infty}h[l]x_m[n-l-mN]\\
&=\sum_{m=-\infty}^{\infty}h[n]*x_m[n-mN]
\end{aligned}
\]
记\(y_m[n]=h[n]*x_m[n]\),则上式可写为
\[
y[n]=\sum_{m=-\infty}^{\infty}y_m[n-mN]
\]

该式表示卷积结果等于\(h[n]\)与\(x_m[n]\)卷积，然后将这些卷积结果移位相加。

可知\(mN\backsim mN+M-2\)共\(M-1\)点是重叠的，这些点要加起来，所以具体算法是:将\(x[n]\)以\(N\)为长度划分为若干组\(x_m[n]\)，将这些组分别与\(h[n]\)进行卷积得到\(y_m[n]\),然后将这些卷积结果进行移位，重叠部分要相加，这就是重叠相加法。

上述提到的\(x_m[n]\)与\(h[n]\)的卷积，均可使用上面提到的\(DFT\)实现。

重叠保留法

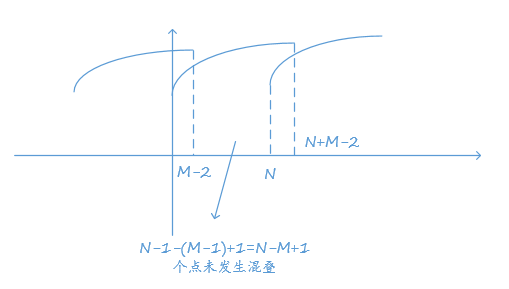
同样将\(x[n]\)以长度\(N\)进行划分，一般取\(N>M\),这时以\(N\)点进行圆周卷积。实际卷积的长度\(l=N+M-1\),由圆周卷积与线性卷积的关系，知圆周卷积的后\(2N-l=N-M+1\)个点与线性卷积的结果是一致的。

取
\[
x_m[n]=\begin{cases}x[n+mL], &0 \leq n \leq N-1 \\
0, &其他\end{cases}
\]

将\(x_m[n]\)与\(h[n]\)进行\(N\)点圆周卷积得到\(y_m[n]\)，只取后\(N+M-1\)个点，其余重叠的前\(M-1\)个点舍弃(保留)。然后进行移位相加，得到的结果就是进行线性卷积的结果。

由上图知，要使得到的结果表示\(y[n]\),应使得\(L-M-2=N-2+1 \Rightarrow L=N-M+1\)

同理上面提到的圆周卷积均可用\(DFT\)进行实现。