---------------------------------------步履不停，奋勇前进！

------------------------难度真的是蛮大丫！后序补充！

ACM的探索之Everything Is Generated In Equal Probability(这真的是很有趣的话语丫！)的更多相关文章

  1. ACM的探索之Everything is Generated In Equal Probability! 后序补充丫！

    Problem Desciption: 百度翻译后的汉化: 参见博客:https://www.cnblogs.com/zxcoder/p/11253099.html https://blog.csdn ...

  2. HDU 6595 Everything Is Generated In Equal Probability (期望dp，线性推导)

    Everything Is Generated In Equal Probability \[ Time Limit: 1000 ms\quad Memory Limit: 131072 kB \] ...

  3. ACM的探索之Keen On Evrything But Triangle（我觉得可以很接近啦！！）

    #include<bits/stdc++.h> using namespace std; int main() { int n,q,l,r; while(cin>>n>& ...

  4. 【HDOJ6595】Everything Is Generated In Equal Probability（期望DP）

    题意:给定一个N,随机从[1,N]里产生一个n, 然后随机产生一个n个数的全排列,求出n的逆序数对的数量并累加ans, 然后随机地取出这个全排列中的一个子序列,重复这个过程,直到为空,求ans在模99 ...

  5. hdu多校第二场 1005 （hdu6595） Everything Is Generated In Equal Probability

    题意: 给定一个N,随机从[1,N]里产生一个n,然后随机产生一个n个数的全排列,求出n的逆序数对的数量,加到cnt里,然后随机地取出这个全排列中的一个非连续子序列(注意这个子序列可以是原序列),再求 ...

  6. HDU-多校2-Everything Is Generated In Equal Probability(公式+逆元)

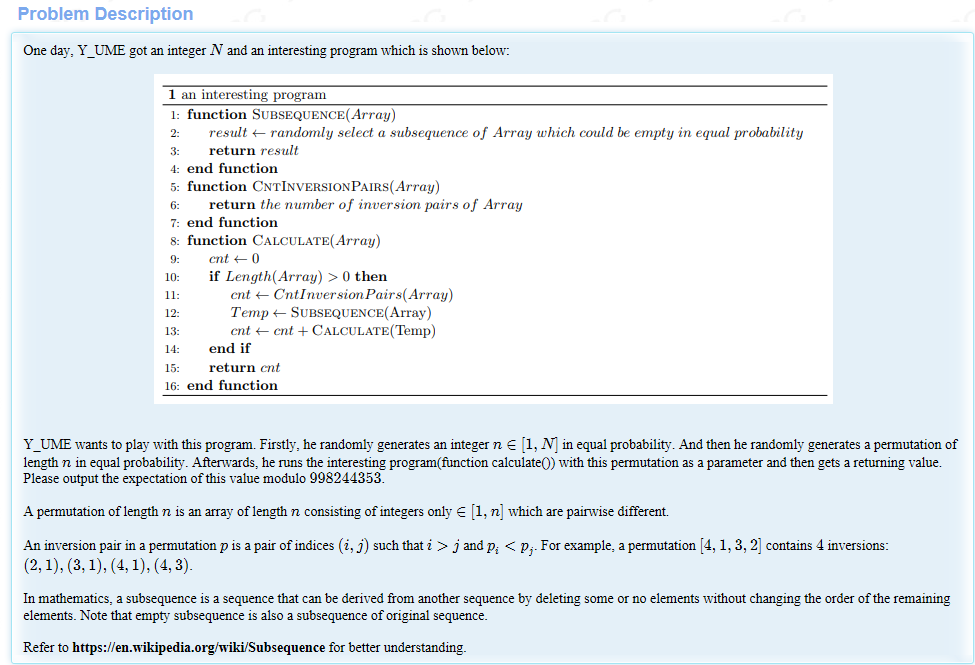
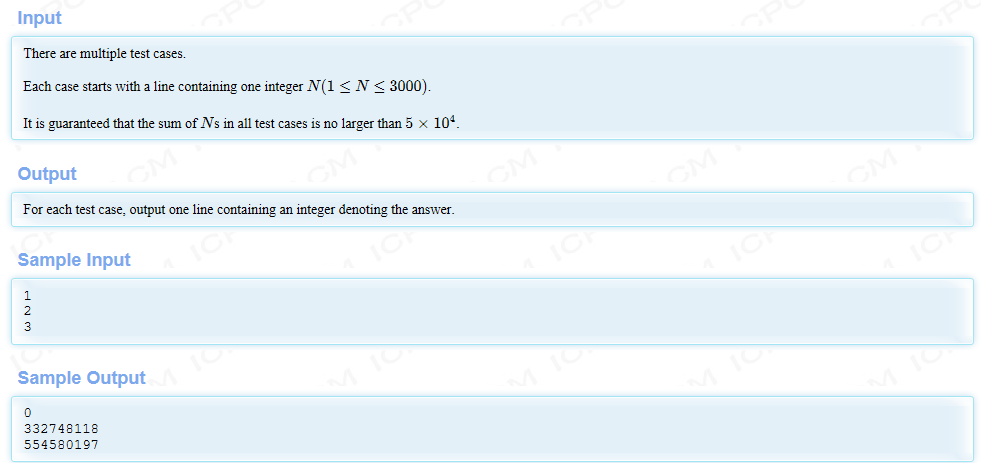
    Problem Description One day, Y_UME got an integer N and an interesting program which is shown below: ...

  7. [hdu6595]Everything Is Generated In Equal Probability

    计算一对逆序对的贡献,即在n个数期望要删多少步才能删掉其中的两个数,设f(n)表示此时的期望,则有方程$f[n]=3/4+(\sum_{i=2}^{n}f[i]\cdot c(n-2,i-2))/2^ ...

  8. ACM的探索之Just Skip The Problem

    -----------------心怀虔诚,奋勇前进,fighting!!!!!! Problem Description: inclusively:          包括一切地;包含地 simul ...

  9. ACM一年记，总结报告（希望自己可以走得很远)

    一. 知识点梳理 (一) 先从工具STL说起: 容器学习了:stack,queue,priority_queue,set/multiset,map/multimap,vector. 1.stack: ...

随机推荐

  1. How to write a paper in a weekend - by Prof. Pete Carr

    Key points: don't procrastinate; review the notes and renew the literature search; determine who you ...

  2. AntDesign(React)学习-13 Warning XX should not be prefixed with namespace XXX

    有篇UMI入门简易教程可以看看:https://www.yuque.com/umijs/umi/hello 程序在点击操作时报了一个Warning: [sagaEffects.put] User/up ...

  3. 二分-E - Rikka with Mutex

    E - Rikka with Mutex Sometimes, technical terms implicate some life philosophy. Mutex is one of them ...

  4. opencv 实现人脸检测（harr特征）

    我这里用的是已经训练好的haar级联分类器. 眼睛检测 haarcascade_eye_tree_eyeglasses.xml 人脸检测 haarcascade_frontalface_alt2.xm ...

  5. python：文件读写

    #!/usr/bin/python# -*- coding:utf-8 -*- #!/usr/bin/python# -*- coding:utf-8 -*- file1 = open('a.txt' ...

  6. office2019与Visio2016不能共存解决办法

    我们电脑已经安装office2019,可是安装visio2016就会安装不了.只要两个软件同时安装就可以解决了,简单粗暴. 首先把电脑的offic或者visio都卸载了,删除干净. 然后先打开visi ...

  7. （转）HDFS简介

    转自:http://os.51cto.com/art/201212/369564.html

  8. Jarvis OJ - 栈系列部分pwn - Writeup

    最近做了Jarvis OJ的一部分pwn题,收获颇丰,现在这里简单记录一下exp,分析过程和思路以后再补上 Tell Me Something 此题与level0类似,请参考level0的writeu ...

  9. unity命令行参数

    Typically, Unity will be launched by double-clicking its icon from the desktop but it is also possib ...

  10. 深度学习之numpy.poly1d()函数

    1.np.poly1d()此函数有两个参数: 参数1:为一个数组,若没有参数2,则生成一个多项式,例如: p = np.poly1d([2,3,5,7]) print(p)    ==>> ...