【C&数据结构】---关于链表结构的前序插入和后序插入

刷LeetCode题目，需要用到链表的知识，忽然发现自己对于链表的插入已经忘得差不多了，以前总觉得理解了记住了，但是发现真的好记性不如烂笔头，每一次得学习没有总结输出，基本等于没有学习。连复盘得机会都没有，花了一个上午得时间重新整理了下，如下：

单链表

单链表应该是最简单得链式结构了，应用广泛也十分简单，这里需要注意单链表常用得前序插入和后序插入，要从根本原理上理解

1. 后序插入

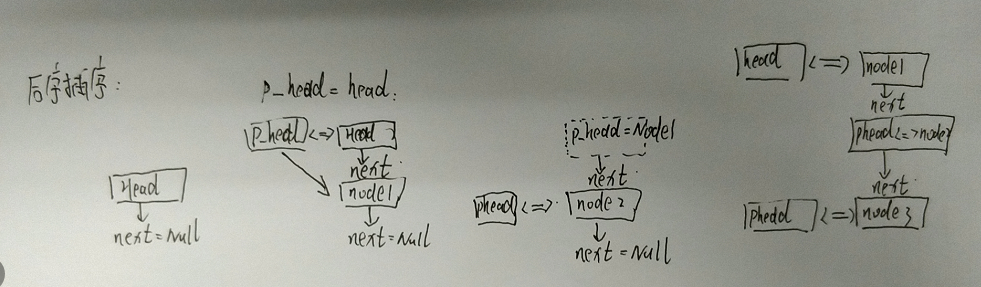
下面分析后续插入得流程：

　　step1: 初始化一个Head节点

　　step2: 创建第一个Node1,后续插入得意思每次一个新的节点应该是当作原始链表得尾巴节点插入，那么很明显Node1->next = NULL；现仅有Head节点和Node1节点，Node1节点还是尾巴，那么接下来怎么作呢？很明显Head->next = Node1;第一步插入操作完成。由于每次插入均要插入到尾巴去，那么我们必须要知道尾巴得位置才可以，不然你怎么插入，因此在这里我们引入了phead变量，这个变量应该要时刻指向链表得尾巴节点。由于最开始是是指向head得，所以起了这么个变量

　　step3:创建第二个节点Node2,同理，Node2->next = 0; phead是指向链表尾巴得节点，phead->next = Node2; 到此完成插入，为了保证下次插入，phead = Node2;

　　step4:同理创建添加。

　　…………

代码如下：

 void Solution::creatList(ListNode *head)
 {
 /*
     后续插入
 */
     ListNode *phead = head;
     for(int i=; i<; i++)
     {
         ListNode *node = new ListNode;
         node->val = i;
         node->next = NULL;
         phead->next = node;
         phead = node;
     }
 } 

后续插入得要点：

　　1) 每次插入均是在当前列表得尾巴插入，所以”尾巴->next = Node(new)“，一步插入成功

　　2) 一次插入成功后，为了保证下次还能插入成功，你要给一个临时指针变量phead在插入成功，将其指向最后一个节点，

　　3) 上述两个要点为一次完整一次插入，并且保证了下次插入也可成功

　　4) 结合上图，Head之后一次是Node1，Node2，...，即后续插入

2. 前序插入

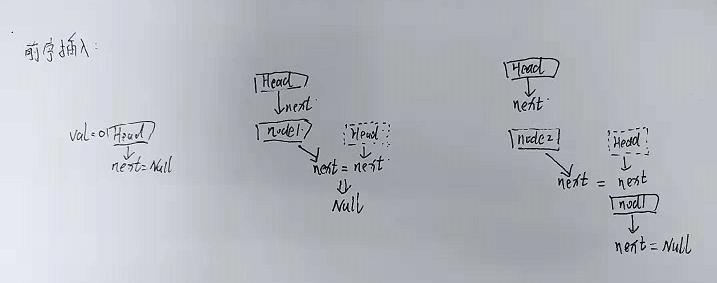
前序插入得流程：

　　Step1: 创建头节点，Head；前序插入得关键在于时刻改变Head->next得指向

　　Step2: 创建Node1节点，让Node1->next = Head->next；这样得操作，我们备份了原Head->next得指向，这样也就解放了Head->next，然后令Head->next = Node1；到此就完成了一次插入

　　Step3: 创建Node2节点，让Node2->next = Head->next（此时Head->next指向得是Node1）；这也就把Node2和Node1链接起来了，然后再让Head->next = Node2; 再次完成插入

　　Step4: 可以看到，Head下依次是Node2, Node1，每次插入都在上次节点得前面，即为前序插入

前序插入得要点：

　　1. 时刻改变Head->next得指向

代码如下：

 void Solution::creatList(ListNode *head)
 {
 /*
     前序插入
     新建个节点指向原head节点的指向，然后让head->next指向新建的node
 */

     ListNode * phead = head;
     for(int i=; i<; i++)
     {
         ListNode *node = new ListNode;
         node->val = i;
         node->next = phead->next;
         phead->next = node;
     }
 }

以上为单链表前插和后插得知识点总结，仅作备份参考。