BFS和DFS详解以及java实现(转载)

作者：Leo-Yang

原文都先发布在作者个人博客：http://www.leoyang.net/

本文版权归作者和博客园共有，欢迎转载，但未经作者同意必须保留此段声明，且在文章页面明显位置给出原文连接，否则保留追究法律责任的权利.

前言

图在算法世界中的重要地位是不言而喻的，曾经看到一篇Google的工程师写的一篇《Get that job at Google!》文章中说到面试官问的问题中几乎有一半的问题都可以用图的方法去解决。由此也可以看出图确实适用范围确实很广。

图的表示

闲话不多说，首先要介绍的就是图的表示，图最常用的两种表示方法是邻接表和邻接矩阵。顾名思义，这两种办法分别用表和矩阵的方式描述图中各顶点之间的联系

下图展示了两种表示上面这个图的方法

BFS

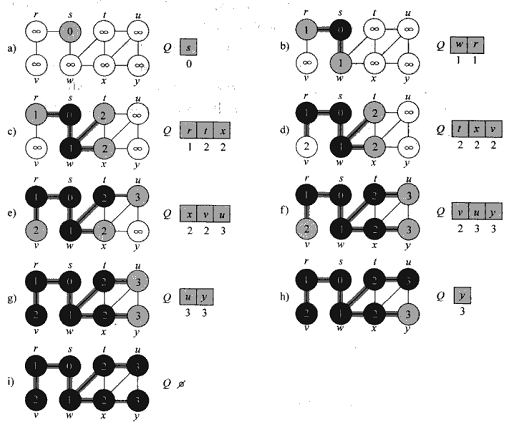
本文将着重介绍遍历图的两种最常用的方法，分别为广度优先遍历和深度优先遍历，后面会具体介绍为什么这么命名。首先来看广度优先遍历BFS（Breadth First Search），其主要思想是从起始点开始，将其邻近的所有顶点都加到一个队列（FIFO）中去，然后标记下这些顶点离起始顶点的距离为1.最后将起始顶点标记为已访问，今后就不会再访问。然后再从队列中取出最先进队的顶点A，也取出其周边邻近节点，加入队列末尾，将这些顶点的距离相对A再加1，最后离开这个顶点A。依次下去，直到队列为空为止。从上面描述的过程我们知道每个顶点被访问的次数最多一次（已访问的节点不会再访问），而对于连通图来说，每个顶点都会被访问。加上每个顶点的邻接链表都会被遍历，因此BFS的时间复杂度是Θ（V+E），其中V是顶点个数，E是边数，也就是所有邻接表中的元素个数。为了更好的说明这个过程，下图列出了对一个图的BFS的过程

private static void bfs(HashMap<Character, LinkedList<Character>> graph,HashMap<Character, Integer> dist,char start)
{
    Queue<Character> q=new LinkedList<>();
    q.add(start);//将s作为起始顶点加入队列
    dist.put(start, 0);
    int i=0;
    while(!q.isEmpty())
    {
        char top=q.poll();//取出队首元素
        i++;
        System.out.println("The "+i+"th element:"+top+" Distance from s is:"+dist.get(top));
        int d=dist.get(top)+1;//得出其周边还未被访问的节点的距离
        for (Character c : graph.get(top)) {
            if(!dist.containsKey(c))//如果dist中还没有该元素说明还没有被访问
            {
                dist.put(c, d);
                q.add(c);
            }
        }
    }
}

运行结果：

从运行结果我们也可以看到，w r作为距离为1的顶点先被访问，x t v其后，最后访问y u。上面的代码使用了一个小的trick，用dist这个hash表来记录每个顶点离s的距离，如果dist中没有这个元素则说明还未被访问，这时将距离写入dist中。BFS访问得到的每个节点与起始顶点的距离是起始顶点到达该顶点的最短距离。从感性认识上来说，BFS向外扩散的方式得到的距离就是最短距离。详细的证明过程请参考CLRS上的相应章节

DFS

DFS（Depth First Search）深度优先搜索是从起始顶点开始，递归访问其所有邻近节点，比如A节点是其第一个邻近节点，而B节点又是A的一个邻近节点，则DFS访问A节点后再访问B节点，如果B节点有未访问的邻近节点的话将继续访问其邻近节点，否则继续访问A的未访问邻近节点，当所有从A节点出去的路径都访问完之后，继续递归访问除A以外未被访问的邻近节点。因为是递归过程，所以我们用过程图看一下也许会更直观一些。

如下是DFS的代码及运行结果

private static void dfs(HashMap<Character , LinkedList<Character>> graph,HashMap<Character, Boolean> visited)
{
    visit(graph, visited, 'u');//为了和图中的顺序一样，我认为控制了DFS先访问u节点
    visit(graph,visited,'w');
}
private static void visit(HashMap<Character , LinkedList<Character>> graph,HashMap<Character, Boolean> visited,char start)
{
    if(!visited.containsKey(start))
    {
        count++;
        System.out.println("The time into element "+start+":"+count);//记录进入该节点的时间
        visited.put(start, true);
        for (char c : graph.get(start))
        {
        if(!visited.containsKey(c))
        {
            visit(graph,visited,c);//递归访问其邻近节点
        }
        }
        count++;
        System.out.println("The time out element "+start+":"+count);//记录离开该节点的时间
    }
}

运行结果：

我们通过一个全局变量count记录了进入每个节点和离开每个节点的时间，我们也可以看到进出元素的时间和过程图中的访问过程是一样的。

总结

总的来说，BFS多用于寻找最短路径的问题，DFS多用于快速发现底部节点。以后若有时间再贴几道相关的题目上来。

作者：Leo-Yang

原文都先发布在作者个人博客：http://www.leoyang.net/

本文版权归作者和博客园共有，欢迎转载，但未经作者同意必须保留此段声明，且在文章页面明显位置给出原文连接，否则保留追究法律责任的权利