51nod 1421 最大MOD值（高妙的调和级数复杂度）

有一个a数组，里面有n个整数。现在要从中找到两个数字(可以是同一个) ai,aj ，使得 ai mod aj 最大并且 ai ≥ aj。

Input

单组测试数据。
第一行包含一个整数n，表示数组a的大小。(1 ≤ n ≤ 2*10^5)
第二行有n个用空格分开的整数ai (1 ≤ ai ≤ 10^6)。

Output

输出一个整数代表最大的mod值。

Input示例

3
3 4 5

Output示例

2

题解：首先考虑mod的真正定义
a%b=a/b*b+c
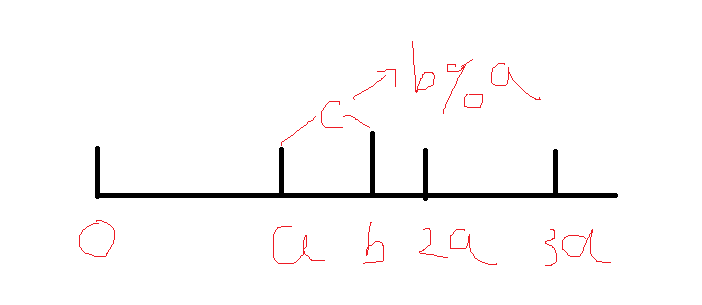
思考一下其实是kb+c的形式，画在数轴上就是

很显然，如果有一个数x%a>b%a他肯定会在(k*a+b,(k+1)*a)的区间之中，到底有没有这些数存在可以用前缀和O(1)查询

所以因此我们就可以对c即余数进行二分了，不过二分的时候检验是O(nlogn)的，因为会枚举每一个数的倍数的区间，总复杂度大约是调和级数即logn 但其实仔细一想这是不满的

在套上二分，复杂度是O(nlognlogn) 

代码如下：

#pragma GCC optimize("inline",3)
#include<cstdio>
#include<cstring>
#include<iostream>
#include<algorithm>
using namespace std;

int vis[],sum[],k,n,a[],cnt;

int check(int x)
{
    for(register int i=;i<=cnt;++i)
    {
        for(register int j=a[i];j<=1e6;j+=a[i])
        {
            if(sum[j+a[i]-]-sum[j+x-]>)
            {
                return ;
            }
        }
    }
    return ;
}

int main()
{
    scanf("%d",&n);
    int tmp;
    for(register int i=;i<=n;++i)
    {
        scanf("%d",&tmp);
        if(!vis[tmp])
        {
            vis[tmp]=;
        }
    }
    for(register int i=;i<=2e6;++i)
    {
        sum[i]=sum[i-]+vis[i];
    }
    for(int i=;i<=1e6;i++)
    {
        if(vis[i])
        {
            a[++cnt]=i;
        }
    }
    register int l=,r=2e6,mid;
    while(l<r)
    {
        int mid=(l+r)>>;
        if(check(mid))
        {
            l=mid;
        }
        else
        {
            r=mid-;
        }
        if(r-l<=)
        {
            r=check(r)?r:l;
            break;
        }
    }
    printf("%d\n",r);
}

这个程序1e5跑跑是非常轻松的但是到了2e5就有点力不从心了

直接提交到51nod上就大概只能过18个点

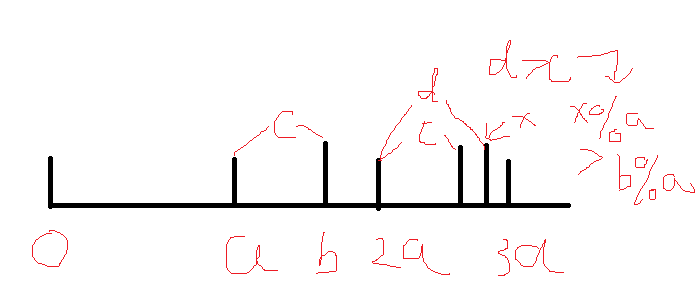
于是考虑优化，其实只要知道了上面那个mod的定义，我们每次对于(k+1)*ai找到小于它的最大aj，那么这个aj%ai的值肯定是(k*ai,(k+1)*ai)区间内所有数%ai最大的

因此我们可以先预处理出f[i]为比i小的最大ai，然后在向上面一样枚举区间对于每个区间计算最大模数更新答案，因为省去了二分，复杂度就是O(nlogn)

代码如下：

#include<cstdio>
#include<cstring>
#include<iostream>
#include<algorithm>
using namespace std;

int b[],a[],n,t,ans=-;

int cmp(int a,int b)
{
    return a>b;
}

int main()
{
    scanf("%d",&n);
    for(int i=;i<=n;i++)
    {
        scanf("%d",&a[i]);
    }
    sort(a+,a+n+,cmp);
    int t=unique(a+,a+n+)-a-;
    n=t;
    int j=;

    for(int i=2e6;i>=;i--)
    {
        while(j<=n&&a[j]>=i) j++;
        b[i]=a[j];
    }
    for(int i=;i<=n;i++)
    {
        for(int j=;j<=2e6/a[i];j++)
        {
            ans=max(ans,b[a[i]*j]%a[i]);
        }
    }
    printf("%d\n",ans);
}

 

yzy大佬用set随手A掉了此题
详见这里
https://blog.csdn.net/yzyyylx/article/details/81013038