机器学习实战笔记(Python实现)-07-模型评估与分类性能度量

1、经验误差与过拟合

通常我们把分类错误的样本数占样本总数的比例称为“错误率”(error rate)，即如果在m个样本中有a个样本分类错误，则错误率E=a/m；相应的，1-a/m称为“精度”(accuracy)，即“精度=1一错误率”。更一般地，我(学习器的实际预测输出与样本的真实输出之间的差异称为“误差”(error)，学习器在训练集上的误差称为“训练误差”(training error)或“经验误差”(empirical error)，在新样本上的误差称为“泛化误差”(generalization error)。显然，我们希望得到泛化误差小的学习器，然而，我们事先并不知样本是什么样，实际能做的是努力使经验误差最小化。

“过拟合”（overfitting）与“欠拟合”（underfitting），学习器把训练样本学得太好了的时候，很可能已经把训练样本自身的一些特点当作了所有潜在样本都会有的一般性质，这样就会导致泛化能力下降。这种现象在机器学习中称为过拟合，相对地，欠拟合是指对训练样本的一般性质尚未学好。

2、评估方法

通常，我们可通过实验测试来对学习器的泛化误差进行评估并进而做出选择。即对数据集D进行适当处理，从中产生出训练集S和测试集T。下面介绍几种常见的做法。

2.1 留出法

“留出法”（hold-out）直接将数据集D划分为两个互斥的集合，分别作为训练集S和测试集T，即D=S υ T，S ∩ T=Φ。在S上训练出模型后，用T来评估其测试误差，作为对泛化误差的估计。常见做法是将大约2/3~4/5的样本用于训练，剩余样本用于测试。

2.2 交叉验证法

“交叉验证法”(cross validation)先将数据集D划分为k个大小相似的互斥子集，即，每个子集Di都尽可能保持数据分布的一致性，即从D中通过分层采样得到，然后，每次用k-1个子集的并集作为训练集，余下的那个子集作为测试集这样就可获得k组训练/测试集，从而可进行k次训练和测试，最终返回的是这k个测试结果的均值。通常把此过程称为“k折交叉验证”(k-fold cross validation)。

Python实现：

from sklearn.cross_validation import train_test_split
# 避免过拟合，采用交叉验证，验证集占训练集20%，固定随机种子（random_state)
train_X, test_X, train_y, test_y = train_test_split(train_dataSet,
                                                    train_label,
                                                    test_size = 0.2,
                                                    random_state = 0)

2.3 自助法

“自助法”（bootstrapping）直接以自助采样法（bootstrap sampling）为基础，它是一个很好解决在留出法和交叉验证法中，由于保留了一部分样本用于测试，导致训练样本规模不同造成影响的解决方案。采样过程为：从给定包含m个训练样本的数据集D中，有放回地抽取m个样本形成数据集D'。显然，D中有一部分样本会在D'中多次出现，而另一部分样本不出现。可以做一个简单的估计，样本在m次采用中不被采到的概率取极限是：

即通过自助采样，实际评估的模型与期望评估的模型都使用m个训练样本，而我们仍有数据总量约1/3的没在训练集中初一的样本用于测试。这样的测试结果也称为“包外估计”（out-of-bag estimate）。

自助法在数据集较小，难以有效划分训练/测试集时很有用；此外，自助法能从初始数据集中产生多个不同的训练集，这对集成学习等方法有很大的好处。然而，自助法产生的数据集改变了初始数据集的分布，这会引入估计偏差，因此，在初始数据量足够时，留出法和交叉验证法更常用一些。

3、性能度量

对学习器的泛化性能进行评估，不仅需要有效可行的实验评估方法，还要有衡量模型泛化能力的评价标准，这就是性能度量（performance measure）。

3.1 错误率与精度

分类错误率定义为：

　　

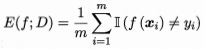
精度则为：

　　

3.2 混淆矩阵

下图是一个二类问题的混淆矩阵，其中的输出采用了不同的类别标签

常用的衡量分类性能的指标有：

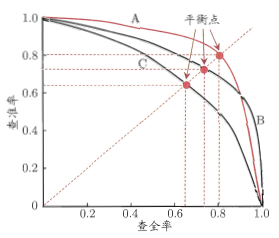
• 正确率（Precision），它等于 TP/(TP+FP) ，给出的是预测为正例的样本中的真正正例的比例。
• 召回率（Recall），他等于 TP/(TP+FN)，给出的是预测为正例的真实正例占所有真实正例的比例。

正确率和召回率也称为查准率和查全率，它们是一对矛盾的度量。一般来说，正确率高时，召回率往往偏低，反之也是。关系如下图

3.3 ROC与AUC

ROC全称是“受试者工作特征”（Receiver Operating Characteristic）曲线，其横轴是“假正例率”（False Positive Rate，简称FPR），纵轴是“真正例率”（True Positive Rate，简称TRP），两者分别定义为：

ROC曲线给出的是当阈值变化时假阳率和真阳率的变化情况。左下角的点所对应的是将所有样例判为反例的情况，而右上角的点对应的则是将所有样例判为正例的情况。虚线给出的是随机猜测的结果曲线。

对不同的ROC曲线进行比较的一个指标是曲线下的面积（Area Unser the Curve）。AUC给出的是分类器的平均性能值，当然它并不能完全代替对整条曲线的观察。一个完美分类器的AUC为1.0，而随机猜测的AUC则为0.5。

3.4 均方误差

回归任务最常用的性能度量是“均方误差”（mean squared error）

THE END.