使用Skyworking 作全链路api调用监控，Integration of Skyworking, auditing the whole chain circuit.

Applicable scenario:



Structure Map

~

Skywalking uses elasticsearch to store data, don't mistake elasticsearch cluster name and host url port, as well as firewall policies when run.

Client, client side

Install-Package Skywalking.AspNetCore -version 0.3.0

    public static class SkywalkingExtensions
    {

        public static IServiceCollection UseEPSkywalking(this IServiceCollection src, IConfigurationRoot appConfigurationRoot)
        {
            if (appConfigurationRoot == null) throw new ArgumentNullException("appConfigurationRoot");
            src.AddSkyWalking(option =>
            {
                option.ApplicationCode = appConfigurationRoot["EPConfig:ServiceName"];
                option.DirectServers = appConfigurationRoot["EPConfig:Skywalking:DirectServers"];

            });
            return src;
        }
    }

At last, audit services on UI:

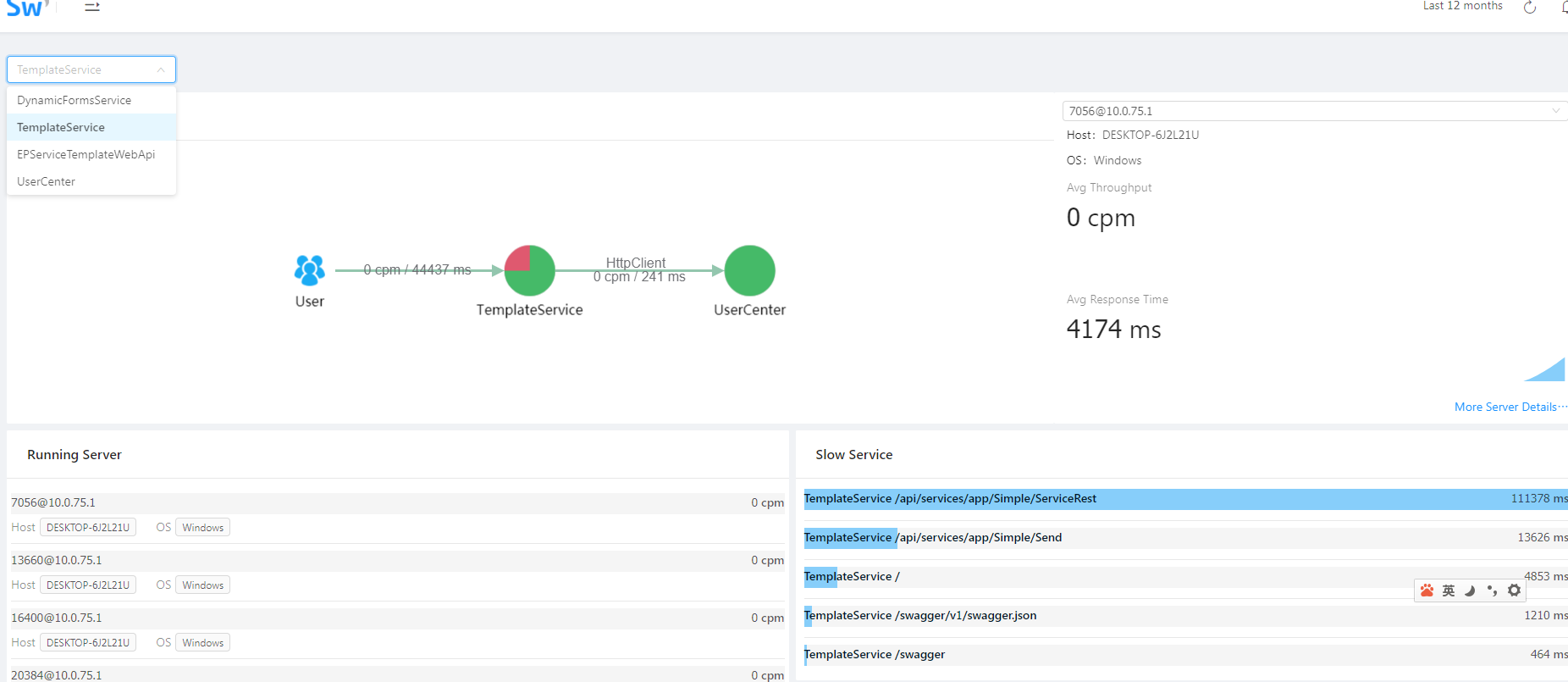
To be continued...