【洛谷】P2725 邮票 Stamps（dp）

题目背景

给一组 N 枚邮票的面值集合（如，{1 分，3 分}）和一个上限 K —— 表示信封上能够贴 K 张邮票。计算从 1 到 M 的最大连续可贴出的邮资。

题目描述

例如，假设有 1 分和 3 分的邮票；你最多可以贴 5 张邮票。很容易贴出 1 到 5 分的邮资（用 1 分邮票贴就行了），接下来的邮资也不难：

6 = 3 + 3 
7 = 3 + 3 + 1
 
8 = 3 + 3 + 1 + 1 
9 = 3 + 3 + 3 
10 = 3 + 3 + 3 + 1 
11 = 3 + 3 + 3 + 1 + 1 
12 = 3 + 3 + 3 + 3 
13 = 3 + 3 + 3 + 3 + 1

然而，使用 5 枚 1 分或者 3 分的邮票根本不可能贴出 14 分的邮资。因此，对于这两种邮票的集合和上限 K=5，答案是 M=13。 [规模最大的一个点的时限是3s]

小提示:因为14贴不出来,所以最高上限是13而不是15

输入输出格式

输入格式：

第 1 行： 两个整数，K 和 N。K（1 <= K <= 200）是可用的邮票总数。N（1 <= N <= 50）是邮票面值的数量。

第 2 行 .. 文件末： N 个整数，每行 15 个，列出所有的 N 个邮票的面值，每张邮票的面值不超过 10000。

输出格式：

第 1 行：一个整数，从 1 分开始连续的可用集合中不多于 K 张邮票贴出的邮资数。

输入输出样例

输入样例#1： 复制

5 2
1 3

输出样例#1： 复制

13

说明

题目翻译来自NOCOW。

USACO Training Section 3.1

---------------------------------------------------------------------------------------------------

分析：用dp[i]表示最少用几张牌组成i方程，需要一个小技巧：我们可以将k这个条件转化成求什么时候，需要组成数字i的牌数>k。

　　剩下的话，不难想到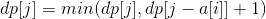，，用这个式子跑循环就可以了。

 #include <cstdio>
 #include <algorithm>
 using namespace std;
 const int maxn=;
 int dp[maxn],a[];//dp[i]：用几张牌组成i
 int main()
 {
     int n,k;
     scanf("%d%d",&k,&n);
     for(int i=;i<=n;i++)
     {
         scanf("%d",&a[i]);
     }
     for(int i=;i<maxn;i++) dp[i]=;
     dp[]=;
     for(int i=;i<=n;i++)
     {
         for(int j=a[i];j<=maxn;j++)
         {
             dp[j]=min(dp[j],dp[j-a[i]]+);
         }
     }
     for(int i=;i<=maxn;i++)
     {
         if(dp[i]>k||dp[i]<)
         {
             printf("%d\n",i-);
             return ;
         }
     }
     return ;
 }