【9.7校内测试】【二分+spfa】【最长上升子序列】【状压DP+贪心（？）】

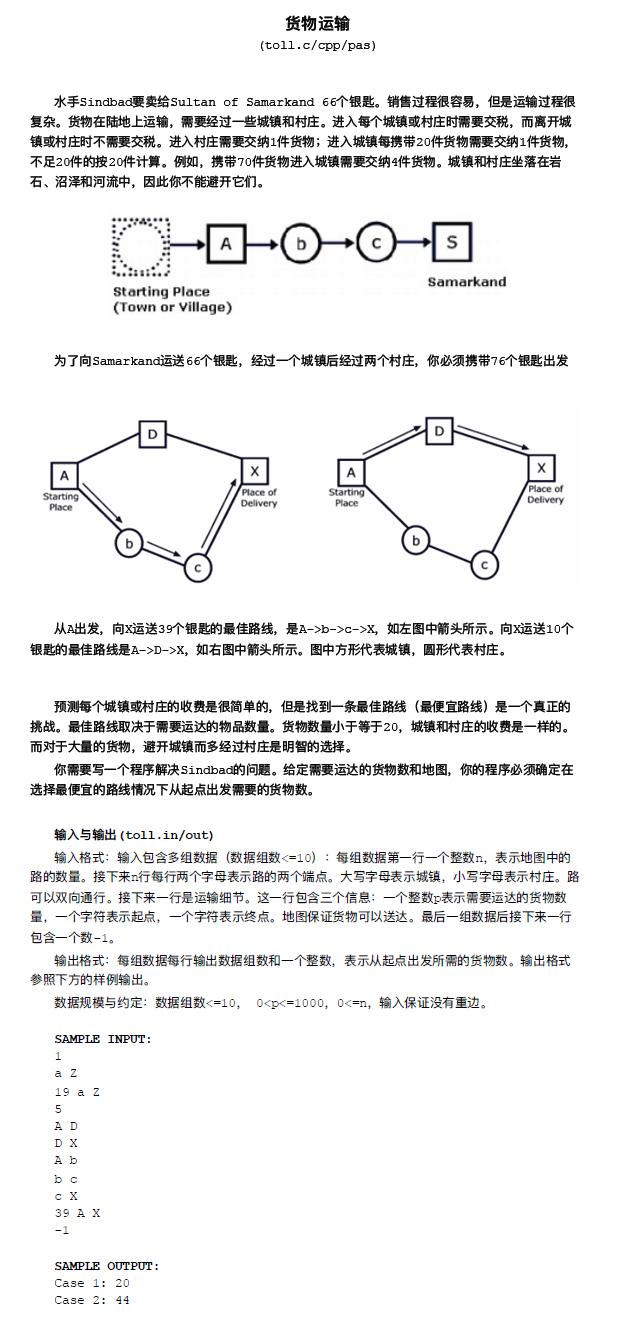
刘汝佳蓝书上的题，标程做法是从终点倒着$spfa$，我是二分答案正着$spfa$判断可不可行。效果是一样的。

【注意】多组数据建边一定要清零啊QAQ！！！

#include<iostream>
#include<cstdio>
#include<cstring>
#include<queue>
using namespace std;

int S, T, p;

struct Node {
    int v, nex;
    Node ( int v = , int nex =  ) :
        v ( v ), nex ( nex ) { }
} Edge[];

int h[], stot;
void add ( int u, int v ) {
    Edge[++stot] = Node ( v, h[u] );
    h[u] = stot;
}

int vis[], dis[];
queue < int > q;
bool Spfa ( int mid ) {
    memset ( vis, , sizeof ( vis ) );
    memset ( dis, -0x3f3f3f3f, sizeof ( dis ) );
    q.push ( S ); vis[S] = ; dis[S] = mid;
    while ( !q.empty ( ) ) {
        int u = q.front ( ); q.pop ( ); vis[u] = ;
        for ( int i = h[u]; i; i = Edge[i].nex ) {
            int v = Edge[i].v;
            if ( v >  && dis[v] < dis[u] -  ) {
                dis[v] = dis[u] - ;
                if ( !vis[v] ) { vis[v] = ; q.push ( v ); }
            } else if ( v <=  && ( dis[v] < dis[u] - ( dis[u] +  ) /  ) ) {
                dis[v] = dis[u] - ( dis[u] +  ) / ;
                if ( !vis[v] ) { vis[v] = ; q.push ( v ); }
            }
        }
    }
    return dis[T] >= p;
}

bool Check ( int mid ) {
    return Spfa ( mid );
}

int erfen ( ) {
    int l = p, r = , ans;
    while ( l <= r ) {
        int mid = ( l + r ) >> ;
        if ( Check ( mid ) ) r = mid - , ans = mid;
        else l = mid + ;
    }
    return ans;
}

int main ( ) {
    freopen ( "toll.in", "r", stdin );
    freopen ( "toll.out", "w", stdout );
    int ti = , n;
    while ( scanf ( "%d", &n ) ==  ) {
        if ( n == - ) break;
        memset ( h, , sizeof ( h ) );
        for ( int i = ; i <= n; i ++ ) {
            char u, v;
            scanf ( "\n%c %c", &u, &v );
            add ( u - 'A', v - 'A' );
            add ( v - 'A', u - 'A' );
        }
        char s, t;
        scanf ( "%d %c %c", &p, &s, &t );
        S = s - 'A'; T = t - 'A';
        int ans = erfen ( );
        printf ( "Case %d: %d\n", ++ti, ans );
    }
}

第一眼看到“最大独立集”，想的完了完了，不会啊怎么办。五分钟后，woc这不就是最长上升子序列吗，好水啊...然后心想这道题班上可能会全a吧，t3要认真才行叻。

结果原来大家都没发现吗...

可以发现每个点到原序列它后面比它小的点都连有一条双向边，要使一个集合里面任意两点都没有连边，在原序列里面这个集合就一定是一个不下降序列。要求最大，那就是最大上升子序列叻...（因为$a[i]$保证不等所以上升就好了

#include<iostream>
#include<cstdio>
#include<algorithm>
#include<cstring>
using namespace std;

int a[], dp[];

int main ( ) {
    freopen ( "sort.in", "r", stdin );
    freopen ( "sort.out", "w", stdout );
    int n;
    scanf ( "%d", &n );
    for ( int i = ; i <= n; i ++ ) scanf ( "%d", &a[i] );
    memset ( dp, 0x3f3f3f3f, sizeof ( dp ) );
    for ( int i = ; i <= n; i ++ ) {
        int pos = lower_bound ( dp + , dp +  + n, a[i] ) - dp;
        dp[pos] = a[i];
    }
    for ( int i = n; i >= ; i -- )
        if ( dp[i] < 0x3f3f3f3f ) { printf ( "%d", i ); break; }
    return ;
}

数据明显是状压，可是发现一个状态要存好多东西存不下怎么办！那就多开几个数组呗...

分别储存每个状态红、绿、白钥匙有多少个，每次更新首先保证所有钥匙的和是最大的，其次保证白钥匙数量最多。

然而是很不严谨的...QAQ（但是数据水我们就不在意这些细节叻~

这样会把一些情况给筛掉，导致后面的情况不能进入。

#include<iostream>
#include<cstring>
#include<cstdio>
#include<algorithm>
using namespace std;

int n;
int Red[(<<)+], Green[(<<)+], White[(<<)+];
int R[], G[], KR[], KG[], W[];

int main ( ) {
    freopen ( "room.in", "r", stdin );
    freopen ( "room.out", "w", stdout );
    scanf ( "%d", &n );
    for ( int i = ; i <= n; i ++ )    scanf ( "%d", &R[i] );
    for ( int i = ; i <= n; i ++ )    scanf ( "%d", &G[i] );
    for ( int i = ; i <= n; i ++ )    scanf ( "%d", &KR[i] );
    for ( int i = ; i <= n; i ++ )    scanf ( "%d", &KG[i] );
    for ( int i = ; i <= n; i ++ )    scanf ( "%d", &W[i] );
    int k0, k1, k2;
    scanf ( "%d%d%d", &k0, &k1, &k2 );
    memset ( Red, -, sizeof ( Red ) );
    memset ( Green, -, sizeof ( Green ) );
    memset ( White, -, sizeof ( White ) );
    Red[] = k0, Green[] = k1, White[] = k2;
    for ( int i = ; i < (  << n ); i ++ ) {
        for ( int j = ; j <= n; j ++ ) {
            if ( ! ( ( i >> ( j -  ) ) &  ) ) {
                int s = i | (  << ( j -  ) );
                int wu = max ( G[j] - Green[i],  );
                if ( wu > White[i] ) continue;
                if ( Red[i] + ( White[i] - wu ) >= R[j] ) {
                    int pre = Red[i] + Green[i] + White[i] - R[j] - G[j] + KR[j] + KG[j] + W[j];
                    int now = Red[s] + Green[s] + White[s];
                    if ( now <= pre ) {
                        int rn = max ( , R[j] - Red[i] ), gn = max ( , G[j] - Green[i] );
                        int wn = rn + gn;
                        if ( now == pre && White[s] > White[i] - wn + W[j] ) continue;
                        Red[s] = max ( , Red[i] - R[j] ) + KR[j], Green[s] = max ( , Green[i] - G[j] ) + KG[j] ;
                        White[s] = White[i] - wn + W[j];
                    }
                }
            }
        }
    }
    int ans = ;
    for ( int i = ; i < (  << n ); i ++ )
        ans = max ( ans, Red[i] + Green[i] + White[i] );
    printf ( "%d", ans );
    return ;
}

正解如下：

#include<cstring>
#include<cstdio>
#include<iostream>
#define fo(i,n) for(int i=0;i<n;i++)
using namespace std;
const int N=;
int dR[N],dG[N],rR[N],rG[N],rW[N],ky[N],n,f[][],z;
int main(){
    freopen("room.in","r",stdin);
    freopen("room.out","w",stdout);
    cin>>n;
    fo(i,n) cin>>dR[i];
    fo(i,n) cin>>dG[i];
    fo(i,n) cin>>rR[i];
    fo(i,n) cin>>rG[i];
    fo(i,n) cin>>rW[i];
    cin>>ky[]>>ky[]>>ky[];
    int sum=ky[]+ky[]+ky[];
    memset(f,-,sizeof f);
    f[][ky[]]=ky[];
    fo(i,<<n){
        int k0=ky[],k1=ky[],r=sum;
        fo(j,n)
            if(i>>j&){
                k0+=rR[j];
                r+=rR[j]+rG[j]+rW[j]-dR[j]-dG[j];
            }
        for(int j=;j<=k0;j++){
            if(f[i][j]==-) continue;
            int fr=f[i][j];
            int k=r-fr-j;
            fo(l,n){
                if(i>>l&) continue;
                int r=max(,dR[l]-j),g=max(,dG[l]-k);
                int &q=f[i|(<<l)][max(,j-dR[l])+rR[l]];
                if(fr>=r+g)
                    q=max(q,fr-r-g+rW[l]);
            }
            z=max(z,j+k+fr);
        }
    }
    cout<<z<<endl;
}

离$AK$只有清零一步之遥5555555，我还是tclQAQ

抱恨离场QAQ